双向增强扩散滤波的图像去噪模型*

汪美玲 周先春石兰芳

(1.南京信息工程大学电子与信息工程学院，南京，210044；2.南京信息工程大学，江苏省大气环境与装备技术协同创新中心,南京,210044；3.南京信息工程大学,江苏省气象探测与信息处理重点实验室,南京,210044；4.南京信息工程大学数学与统计学院，南京，210044)

双向增强扩散滤波的图像去噪模型*

汪美玲1,2,3周先春1,2,3石兰芳4

(1.南京信息工程大学电子与信息工程学院，南京，210044；2.南京信息工程大学，江苏省大气环境与装备技术协同创新中心,南京,210044；3.南京信息工程大学,江苏省气象探测与信息处理重点实验室,南京,210044；4.南京信息工程大学数学与统计学院，南京，210044)

提出一种双向增强扩散滤波的图像去噪模型。简化扩散方程建立双向扩散系数，使模型在扩散过程中能够实现平滑与锐化的双向过程，为加强平滑和锐化强度，用小波变换增强图像，使整体图像轮廓得到增强和局部图像纹理特征得到弱化。然后，对阈值进行了自适应设计和改进，使其根据图像的最大灰度值和迭代次数自动控制阈值，进一步保留图像边缘和细节特征。实验仿真和可行性的验证结果表明，新模型去噪效果较理想，不但能抑制噪声，而且能保护细节信息，峰值信噪比得到了有效的提高，性能更优越。

双向扩散系数；自适应阈值；图像去噪

引 言

当今，许多科学领域都包含着数字图像处理技术，而在偏微分方程(Partial differential equation,PDE)图像去噪算法中，各向异性扩散已成为当前研究热点[1-4]。Perona和Malik[5]在1990年首次令传导系数依赖图像梯度的二阶PDE，建立PM模型。Rudin等[6]在1992年从能量泛函角度建立了能更好地保持图像边缘纹理等细节特征的全变分(Total variation,TV)模型，是PDE在图像去噪中的重要体现。Guy Gilboa 等[7]提出了复模型，是从实数域延伸到复数域的PM模型的改进，该模型能够同时实现前后向扩散，扩大了去除噪声的范围。自从提出PM模型后，近些年来，PDE的图像去噪方法取得了很大的进展[8-10]。最近，出现了许多较新的图像去噪算法，如Buades等提出了非局部平均(Non-local means,NLM)滤波器，该滤波器能够保护图像的纹理特征，但计算复杂、运行效率慢[11]。文献 [12] 提出了块匹配三维协同(Block matching 3D cooperative,BM3D)方法，该方法的峰值信噪比较高，视觉效果很好，但有复杂的时间处理过程。文献[13]提出了基于概率修复(Probablistic patch-based, PPB )滤波器，该滤波器对合成孔径雷达(Synthetic aperture radar, SAR)图像滤波效果较好，但处理效率较低，有过长的滤波过程。针对该问题，又提出了非迭代的PPB滤波方法，该方法虽然解决了处理效率的问题，但该滤波器对图像纹理特征的保持仍有欠缺。本文在经典的扩散模型基础上，建立局部坐标系，对扩散模型进行简化与分析，建立扩散滤波过程，使图像在扩散过程中实现平滑与锐化的双向过程。为了更加突出图像的整体结构，增强边缘的锐化作用，作一些特殊处理，用小波对图像进行分解，在频域里增强图像，对图像进行系数的分解，从而达到图像整体结构的突出和图像细节特征的弱化，然后，对阈值进行了自适应设计，使其根据图像的最大灰度值和迭代次数自动控制阈值。

1 PM和TV模型

1.1 PM模型

Perona和Malik首次提出了PM模型，其能量泛函为

(1)

(2)

(3)

(4)

式中：k为图像的梯度阈值。

1.2TV模型

TV模型是另一种经典的去噪模型，是将其构造的能量泛函转化为偏微分方程来求解，其能量泛函公式为

(5)

式中:I0为原始图像，I为变化中的灰度图像，I为图像像素的梯度，λ为拉格朗日算子，其Euler-lagrange方程为

(6)

用梯度下降流解式(6)，则可得TV模型

(7)

2 改进的模型

2.1 经典扩散模型的简化分析

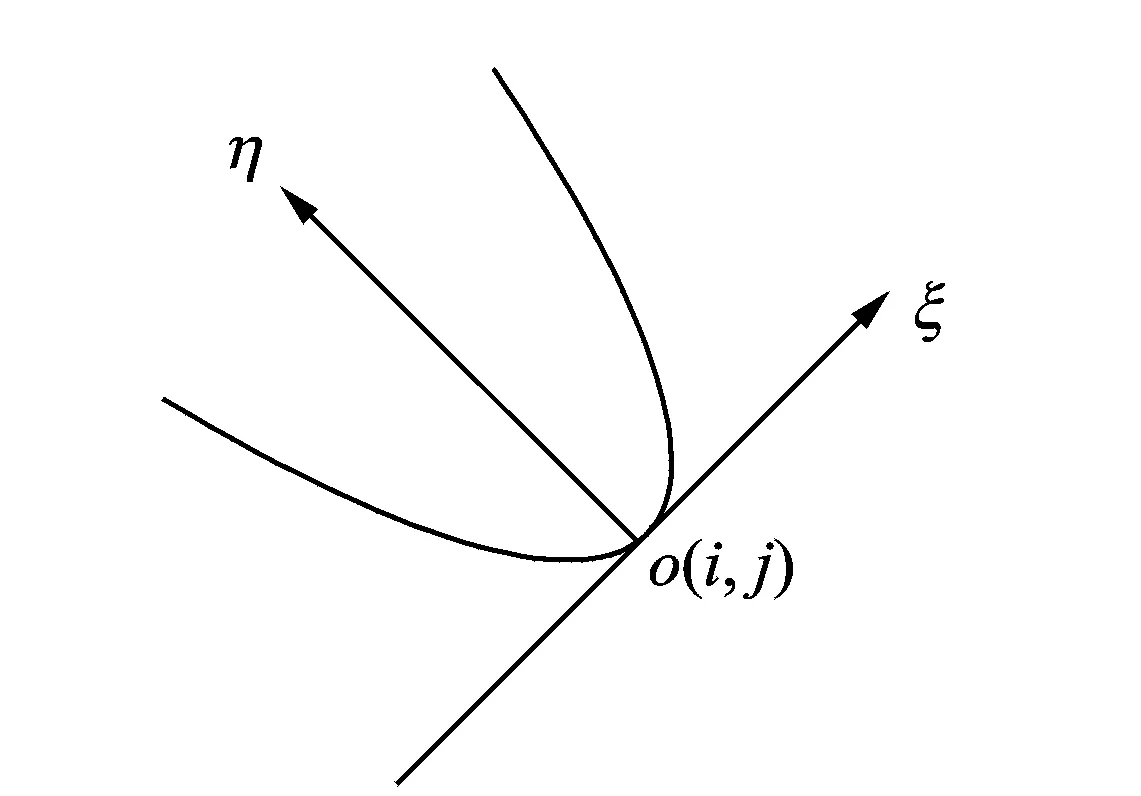
图1 图像中某点局部坐标 Fig．1 Local coordinate of a point of the image

(8)

(9)

(10)

则式(2)最终表达为

(11)

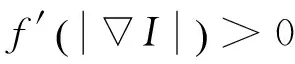
(12)

2.2 新模型建立

根据以上分析对式(11)做进一步简化

(13)

设

(14)

(15)

(16)

由式(16)可知，沿梯度方向逆扩散，锐化图像边缘，改善了边缘模糊的现象，能很好地保护图像的边缘。

(17)

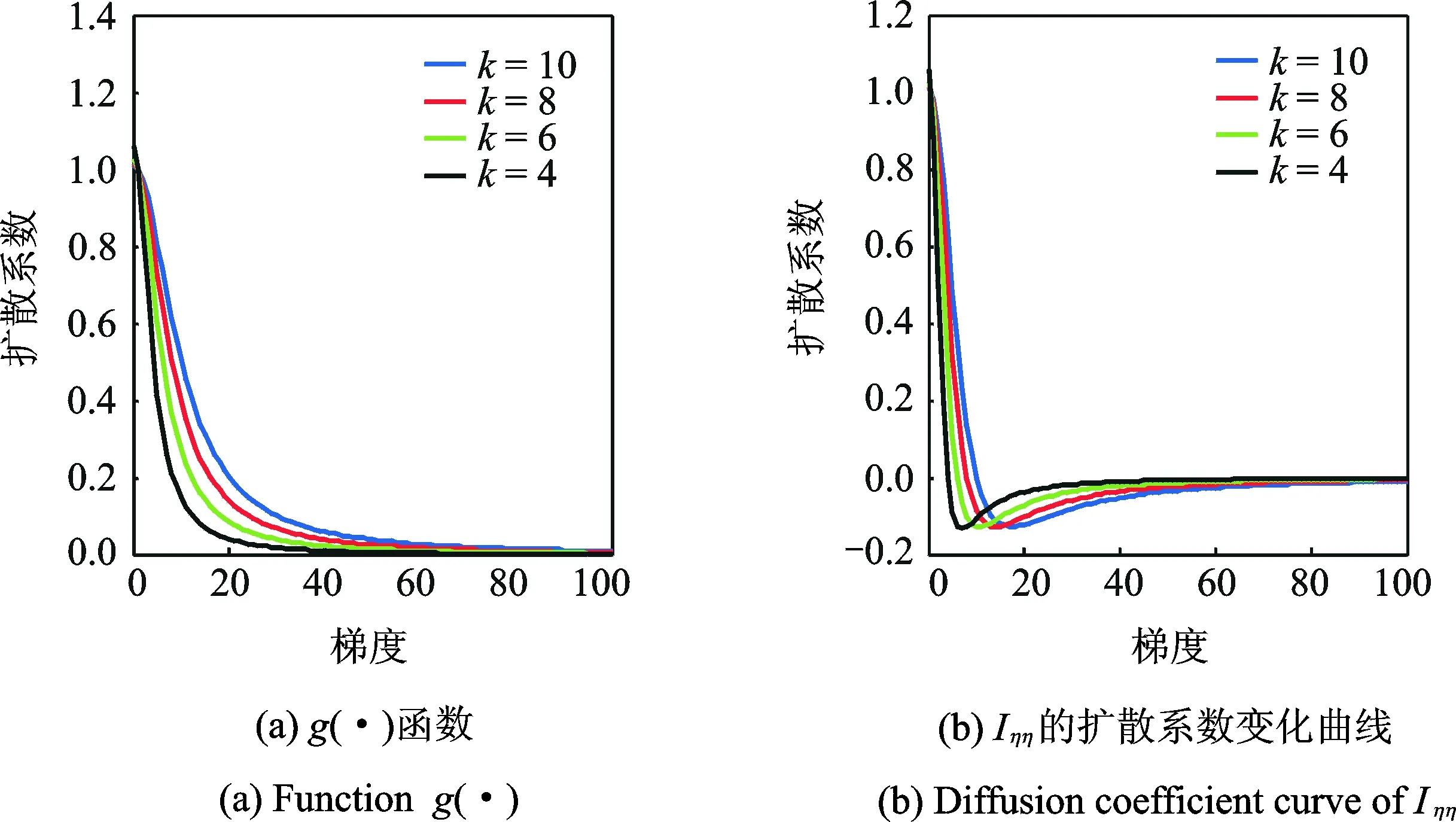
图2 g(·)函数和 Iηη的扩散系数Fig．2 Function g(·) and diffusion coefficient curve of Iηη

由式(17)可知，在图像的平滑区域，该模型转化为了各向同性去噪方程，即在图像的边缘和梯度方向能够达到同时平滑的效果，去噪能力较强。观察梯度方向上Iηη前扩散系数的曲线变化图2(b)所示。由图2(b)可以看出，随着梯度增大，当梯度达到某一值时，扩散系数出现了负值，符合以上的分析过程。本文的整个扩散过程，实质上是通过图像梯度与阈值的大小进行比较实现的，通常在扩散过程中，会预先设定一个梯度阈值k，k一般是个常量，即不论像素点所在区域与相邻区域的灰度值存在怎样的关系，都采用这个预先设定好的常量梯度阈值，从而不能保持图像某些区域的细节特征。随着扩散时间的不断增加，该部分像素点的梯度阈值逐渐减小，为了使边缘和噪声得以区分，当扩散时间增加时，梯度阈值k则相应减小，从而就能在小范围区域内判断边缘位置，能更好地保持图像特征。

综上分析，将梯度阈值k设计为随扩散时间和扩散次数变化的函数，即有

(18)

在滤波过程中为了不让图像失真，给图像添加一项保真项[14]，表示为

(19)

设计的双向增强扩散模型为

(20)

图3 实验原始图像与增强图像 Fig．3 Original and enhanced images of experiment

为了解双向增强扩散模型，采用中心差分法[15]，则双向增强扩散模型的离散化形式为

(21)

式中:n=0,1,2,……,表示时间步长。其中

(22)

(23)

(24)

3 实验结果与分析

(25)

(26)

式中：图像的分辨率为W×H，I和I0分别为原始图像和去噪后的图像，MSE越小越好，PSNR越大越好。

首先对Nuist图像用各算法和本文新模型进行平滑。其中，Δt=0.2，n=30，PM模型中的扩散系数取文章中的式(3)，10为取定的阈值，TV模型中，λ=0.1，新模型中，λ*=5。平滑结果、评价指标和局部放大图分别如图4、表1和图5所示。为了更好地显示滤波前后图像的细节信息情况，采用Canny算子[16]检测各模型滤波结果的图像，实验结果如图6所示。

分别从图像整体与局部放大的可视效果来看，如图4(b),(c)和图5(b),(c)，PM模型处理后的图像中仍含有大量噪声没有被去除，且产生了“块状”效应；TV模型去噪后的图像中出现了一些孔洞，这是由

图4 各模型去噪后图像Fig．4 Denoised image of each model

类别加噪图像PM模型[4]TV模型[5]NLM算法[10]BM3D算法[11]Non-iterativePPB算法[12]IterativePPB算法[12]新模型MSE385.2109222.970377.342571.35527.6887×10-466.138765.31110.5474PSNR22.273824.648329.246629.596531.141529.932529.985950.7474

图5 各模型去噪后局部放大图像Fig．5 Local amplification of denoised images of all models

图6 各模型去噪后边缘提取图像Fig．6 Edge detection of denoised images of all models

于TV模型不满足形态学的原则，从而使图像遭到破坏，但该模型有一定的去噪效果，图像的细节特征保持较好，如图6(c)所示。由4(d)和表1可以看出，尽管NLM算法能较好地去除噪声，但从图5(d)、图6(d)可以看出该算法不能很好地保护原图像的结构信息。图4(e)、图5(e) 和表1显示了BM3D方法有较好的视觉效果和较高的PSNR值，但从图6(e)可知，此方法不能有效地保护图像细节特征。在表1中，Iterative PPB方法去噪性能较好，但在运行过程中花费的时间很长，从而不能有效地应用到实际中，而 Non-iterative PPB方法解决了这个问题，但是该方法不能很好地保护原图像的结构信息，如图6(f)所示。由图4(h)、图5(h)可以看到双向增强扩散模型的可视性最好，主要是由于该模型建立平滑与锐化的双向扩散过程，比较好地考虑图像的局部特征，兼顾了去噪与纹理特征的保护。由表1可知，双向增强扩散模型各项性能最好，与仿真图的效果相同。

用不同强度噪声反映各模型对噪声的去除效果和图像特征保护状况。现对图像添加不同方差的噪声，实验结果如图7所示，由图7可以看出新模型在所有模型中有最高的峰值信噪比和最低的均方差。

图7 不同噪声方差时MSE和PSNR的变化Fig．7 PSNR and MSE with different variance noise for each model

4 结束语

本文在扩散方程的基础上，构建双向扩散系数，建立双向增强扩散滤波模型。该模型在扩散过程中能够实现平滑与锐化的双向过程，为了更加突出图像的整体结构，增强对边缘锐化的作用，做一些特殊处理。首先用小波分解图像，在频域里增强图像，处理分解系数，突出图像的轮廓和整体结构，弱化细节，然后对阈值进行了自适应设计和改进，使其根据图像的最大灰度值和迭代次数自动控制阈值，进一步保留图像边缘和细节特征。仿真实验结果表明，本文新模型能够兼顾图像噪声的去除和细节特征的保护，大幅提高了PSNR，较经典模型去噪性能更优越。

[1] Niang O,Thioune A, Gueirea M C, et al. Partial differential equation-based approach for empirical mode decomposition:Application on image analysis[J]. IEEE Transactions on Image Processing,2012,21(9):3991-3999.

[2] 陈婷婷, 沈民奋, 杨金耀. 一种复合各向异性扩散的图像去噪算法[J].数据采集与处理, 2014, 29 (5): 757-763.

Chen Tingting, Shen Minfen, Yang Jinyao. Algorithm based on compound anisotropic diffusion for image denoising[J]. Journal of Data Acquisition and Processing, 2014, 29 (5): 757-763.

[3] Liu Peng, Huang Fang, Li Guoqing. Remote-sensing image de-noising using partial differential equations and auxiliary images as priors[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9 (3): 358-361.

[4] 周先春, 汪美玲, 石兰芳. 阈值寻优的高保真各向异性滤波模型[J]. 计算机辅助设计与图形学学报, 2016, 28 (9): 1550-1559.

Zhou Xianchun, Wang Meiling, Shi Lanfang. Anisotropic filtering model of high-fidelity based on threshold optimization[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28 (9): 1550-1559.

[5] Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12 (7): 629-639.

[6] Rudin L, Oshers, Fatemi E. Nonlinear total variation based noise removal algorithms [J]. Physic D, 1992, 60 (1-4): 259-268.

[7] Gilboa G. Nonlinear scale space with spatially varying stopping time[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30 (12): 2175-2186.

[8] Chumchob N. Vectorial total variation-based regularization for variational image registration[J]. IEEE Transactions on Image Processing, 2013, 22 (11): 4551-4558.

[9] 陈永彬，宋海英. 基于图像亮度局部约束的总变分图像去噪法[J]. 数据采集与处理, 2011, 26 (5): 564-568.

Chen Yongbin, Song Haiying. Total variation image denoising based on local intensity bound constraints[J]. Journal of Data Acquisition and Processing, 2011, 26 (5): 564-568.

[10] Zhong Junmei, Sun Huifang. Wavelet-based multiscale anisotropic diffusion with adaptive statistical analysis for image restoration[J]. IEEE Transactions on Circuits and System—I: Regular Papers, 2008, 55 (9):2716-2724.

[11] Buades A. A non-local algorithm for image denoising[C]∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego:[s.n.], 2005, 60-65.

[12] Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16 (8): 2080-2095.

[13] Deledalle C A, Denis L, Tupin F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights[J]. IEEE Transactions on Image Processing, 2009, 18 (12): 2661-2672.

[14] 朱立新，王平安，夏德深. 非线性扩散图像去噪中的耦合自适应保真项研究[J]. 计算机辅助设计与图形学学报，2006，18 (10)：1519-1524.

Zhu Lixin, Wang Pingan, Xia Deshen. A study on the coupling adaptive fidelity term in anisotropic diffusion based image denoising[J]. Journal of Computered-Aided Design & Computer Graphics, 2006, 18 (10): 1519-1524.

[15] Ghita O, llea D E, Whelan P F. Adaptive noise removal approach for restoration of digital images corrupted by multimodal noise[J]. IET Image Process let, 2012, 6(8): 1148-1160.

[16] Xu Qian, Varadarajan S, Chakrabarti C, et al. A distributed canny edge detector: Algorithm and FPGA implementation[J]. IEEE Transactions on Image Processing, 2014, 23 (7): 2944-2959.

Image De-noising Model based on Bidirectional Enhanced Diffusion Filter

Wang Meiling1,2,3, Zhou Xianchun1,2,3, Shi Lanfang4

(1. School of Electronic and Information Engineering, Nanjing University of Information Science & Technology, Nanjing, 210044, China; 2. Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing, 210044, China; 3. Jiangsu Key Laboratory of Meteorological Observation and Information Processing, Nanjing University of Information Science and Technology, Nanjing, 210044, China; 4. School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing, 210044, China)

A bidirectional enhanced diffusion filter image de-noising model is presented. The diffusion equation is firstly simplified and analyzed to establish bidirectional diffusion coefficient. Hence, the two-way process of smoothing and sharpening can be achieved by the model in the diffusion process, To further enhance the strength of the smoothing and sharpening, image enhancement is used to enhance the overall outline of the image using wavelet transform, thus weakening texture detail of the image. Then, the threshold will be designed and improved, and it will be automatically controlled by maximum image gray value and iterative times, which can retain the image edge and detail features. The proposed model is be simulated. The experimental result shows that the new model is ideal, and it can improve the performance of de-noising and the protection of edge. The texture detail information is satisfactory. The peak signal to noise ratio is promoted drastically. Therefore,the performance is better than classical algorithms.

bidirectional diffusion coefficient; adaptive threshold; image de-noising

国家自然科学基金(11202106, 61201444)资助项目；教育部高等学校博士学科点专项科研基金(20123228120005)资助项目；江苏省“信息与通信工程”优势学科建设项目;江苏省自然科学基金(BK20131005)资助项目；江苏省青蓝工程和江苏省高校自然科学研究项目(13KJB170016)资助项目。

2014-12-30；

2015-10-12

TP391

A

汪美玲(1989-)，女，硕士研究生，研究方向:图像处理、模式识别，E-mail:Mely nuaa@163.com。

周先春(1974-)，男，博士，副教授，研究方向：信号与信息处理。

石兰芳(1976-)，女，博士，副教授，研究方向：非线性分析。