基于扩张状态观测器的永磁同步电机自适应滑模调速控制
郭一军
(1.浙江工业大学 信息工程学院,杭州 3100321 2.黄山学院 机电工程学院,安徽 黄山 245041)
基于扩张状态观测器的永磁同步电机自适应滑模调速控制
郭一军1,2
(1.浙江工业大学 信息工程学院,杭州 3100321 2.黄山学院 机电工程学院,安徽 黄山 245041)
针对永磁同步电机(permanent magnet synchronous motor,PMSM)调速系统存在参数不确定性及负载扰动问题,提出了一种基于扩张状态观测器的自适应滑模控制方法。在系统模型存在参数不确定性及负载扰动情况下,通过扩张状态观测器对系统的总和扰动进行实时观测,并在控制过程中加以前馈补偿以降低系统总和扰动对控制精度的影响,提高系统的动态性能。由于系统观测误差上界无法精确获得,自适应滑模控制器中的切换控制增益采用参数自适应律来调节,可有效改善系统的抖振现象,保证系统输出高精度跟踪期望信号。仿真结果表明,与传统的比例-积分(proportional-integral,PI)控制方法相比较,提出的基于扩张状态观测器的自适应滑模控制方法具有转速超调量小,响应速度快,对系统的参数不确定性及负载扰动具有很强的抑制力,且能够有效减弱滑模控制的抖振问题和提高系统的鲁棒性能。
永磁同步电机(PMSM); 调速; 滑模控制; 扩张状态观测器; 总和扰动
0 引 言
永磁同步电机(permanent magnet synchronous motor,PMSM)由于具备结构简单、维护方便、电源利用效率高、低噪声、高可靠性等特点,在工业机器人、数控设备、新能源汽车等领域获得了广泛的应用[1]。
针对PMSM调速系统控制算法的研究也备受人们的关注,如常规的算法有比例-积分(proportional-integral,PI)控制算法,但由于PMSM调速系统是易受模型参数变化、负载扰动等内外部不确定因素的影响,常规的PI控制算法已难以满足高性能的控制要求。近年来,人们提出了许多非线性控制策略用于提高系统的稳定性和鲁棒性,如鲁棒控制[2]、智能控制[3-4]、自适应控制[5]、模型预测控制[6-7]、滑模控制[8-10]等。在这些控制方法中,滑模控制作为一种非常有效的非线性系统控制解决策略,有其自身的许多优势,如算法实现简单、计算量小、响应迅速,进入滑动模态后对系统参数变化和外部扰动具有很强的鲁棒性,可有效用于PMSM的调速控制。文献[8]将积分滑模用于PMSM调速系统的设计,消除PMSM调速系统的稳态误差,实现PMSM的稳定调速。文献[9]提出采用可变边界层的快速非奇异滑模控制策略,减小了转速与q轴定子电流一阶模型所引起的误差,实现抖振和跟踪精度的协调控制。文献[10]针对传统滑模抖振现象突出问题,提出采用高阶滑模实现伺服系统的高性能跟踪解决方案。但上述文献采用滑模控制技术设计PMSM调速控制系统,其前提是要求系统所有状态是完全可测的,当系统部分状态不可测时,上述方法将失效。
为了估计系统的未知状态和外部扰动等不确定因素,韩京清[11]提出了自抗扰控制技术,其核心扩张状态观测器在非线性系统控制领域获得了广泛的应用[12-15],它将系统的未知状态和外部扰动等不确定因素扩张为一个新的状态,无需知道不确定因素的任何先验知识,仅利用系统输入输出信息就能实现对被扩张状态的充分估计。
本文利用扩张状态观测能充分观测系统内部未知状态及外部负载力矩变化等不确定性因素,通过对不确定性因素的前馈补偿作用将原系统近似为一个线性系统,并在此基础上再利用自适应滑模控制技术来实现控制器的设计,不仅可有效改善系统抖振现象而且可有效抑制控制器输出量过大问题,提高系统的鲁棒性能。
1 永磁同步电机数学模型及问题描述
假设电机磁场在空间呈正弦分布,磁路不饱和,不考虑铁芯磁滞损耗和涡流损耗情况下,可得PMSM在d-q坐标系下的状态方程[8-9](对于面装式永磁同步电机Ld=Lq=L)为
(1)
(1)式中:id,iq分别为d轴,q轴的定子电流分量;ud,uq分别为d,q轴的定子电压分量;L为定子电感;np为极对数;Rs为定子电阻;φ为转子磁链;J为转动惯量;B为摩擦系数;TL为负载转矩;ω为转子机械角速度。
由于实际系统中摩擦系数未知,且会随现场温度而变化,即模型存在不确定性。同时TL也易受负载扰动影响,所以可以将负载转矩和摩擦系数相关项看成系统的不确定项,加上系统其他一些扰动因素,称之为系统的总和扰动,统一记为N,故 (1)式中第3个方程可重写为
(2)
控制目标为设计有界控制输入,使得PMSM调速系统在有模型误差及外部有界干扰情况下可以稳定准确跟踪预先设定的期望信号,提高系统的鲁棒性。
2 非线性扩张状态观测器设计
2.1 扩张状态观测器设计
(2)式中含有不确定项N,在实际应用中,系统无法准确测量N的值,但可以通过扩张状态观测器快速精确获得N的估计值并进行在线补偿。
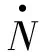
(3)
依据二阶扩张状态观测器[11]的设计思想,(3)式的非线性扩张状态观测器设计为
(4)
(4)式中,e1为扩张状态观测器对系统状态变量的观测误差;z1和z2分别为ω和N的观测状态;β01,β01,α,σ为观测器参数,只要适当选择这些参数,系统(4)就能很好地估计系统(3)中的状态变量。fal(·)为非线性函数,表达式为
(5)
2.2 参数极点配置
依据文献[16],观测器参数β01,β01可由极点配置法确定,设Δ1=z1-ω,Δ2=z2-N,则(4)式减去(3)式可得
(6)
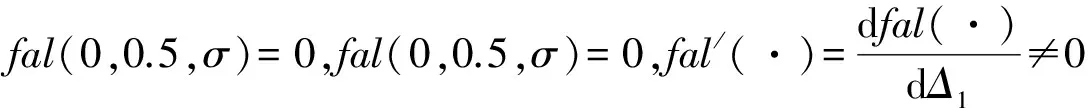
(7)
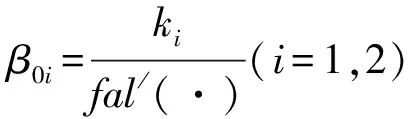
(8)
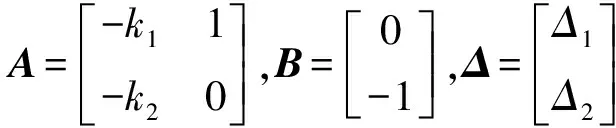

(9)
因此,参数β0i的确定问题转化成参数ki的确定问题。使系统(8)在扰动作用下是渐稳的必要条件是矩阵A的特征根全部处于复平面的左半平面。
若选取系统(8)的期望极点为pi(i=1,2),则参数ki的值可由(10)式得到。
(10)
(10)式中:I为单位矩阵;ζ为系统极点。
故通过极点配置技术选取合适的极点,通过(10)式可以方便地确定ki值。
3 PMSM调速系统控制器设计及稳定性分析
3.1 自适应滑模控制器设计
定义速度跟踪误差变量为
(11)
(11)式中:ωr为期望转速,ω为永磁同步电机实际输出的转子机械角速度。
对(11)式求导,并结合(2)式,可得
(12)
为实现系统误差状态e的镇定控制及PMSM伺服系统的快速高精度响应,滑模面设计为
(13)
(13)式中,λ1>0,λ1为控制参数。对s求导数可得
(14)
由(14)式, 基于扩张状态观测器的普通滑模控制律设计为
(15)
(15)式中,k*>0且需满足k*≥|Δ2|。由于观测误差Δ2上界无法精确获得,k*的值难以准确给定,若该值过大,系统响应速度加快,但抖振增强,系统控制性能变差;若该值过小,抖振减弱,但响应速度变慢,超调量和稳态误差变大,系统控制性能也会变差。为了合理选取该值,本文采用参数自适应的方法,设计基于扩张状态观测器的自适应滑模控制律为
(16)
(16)式中,k为自适应控制器增益,其自适应律表示为

(17)
(17)式中,γ>0为自适应增益。因此,可得自适应控制器增益为
(18)
3.2 稳定性分析
定理1 对于给定系统(2)和滑模面(13),当采用基于扩张状态观测器的自适应滑模控制律(16)及自适应控制增益(18)时,则状态变量ω能够渐近稳定跟踪期望信号ωr。
证明 依据滑动模态的存在条件,利用Lyapunov函数进行稳定性分析,取候选Lyapunov函数为
(19)
对V按时间t求导,并将(3)式,(14)式代入(19)式可得

(20)
将(16)式,(17)式代入(20)式可得
(21)
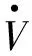
证毕。
4 仿真及结果分析
为了验证所提的基于扩展状态观测器的自适应滑模控制算法的有效性,本文利用Simulink仿真模块分别对ESO+SMC控制算法,ESO+ASMC控制算法及传统PI控制算法进行了仿真对比。PMSM的主要参数为PN=3 kW,UN=200 V,IN=18 A,nN=3 000 r/min,Rs=0.258 Ω,φ=0.057 Wb,B=0 N·m·s,np=5,J=0.006 5 kg·m2,Ld=Lq=3.5 mH。
基于ESO的永磁同步电机自适应滑模控制的示意图如图1所示,其中,ia,ib分别为电机a,b相电源的采样电流。
通过极点配置算法得到的扩张状态观测器的参数设置为k1=120,k2=3 200;ESO+SMC方法参数设置为λ1=10,k*=30;ESO+ASMC方法参数设置为λ1=10,γ=0.4;PI速度控制器参数设置为kp=0.5,ki=2.5。

图1 基于ESO的永磁同步电机自适应滑模控制Fig.1 Adaptive sliding mode control of PMSM based on extended state observer
仿真给定转速ωr=600 rad/min,当系统运行至4 s时负载转矩发生突变,并在运行至6 s时加以撤销,用于模拟系统所受的总和扰动。所得仿真结果如图2-图5所示,图2为速度响应曲线;图3为扩展状态观测器对系统总和扰动的观测曲线;图4为q轴电流信号;图5为参数自适应曲线。由图2a和图2b可以看出,当没有系统扰动时前2种控制方法都能很好地跟踪期望信号,当系统存在突发扰动时,方法2具有更小的跟踪误差且调节时间也更短。由图2c可见,所提控制算法与PI控制算法相比,当突加负载扰动时具有更小的超调量及更短的响应时间,从而表明本文所提方法好的鲁棒性能。由图3可以看出,只要适当选取ESO的参数,2种方法中扩展状态观测器就能很好地观测扰动信号。对比图4中的q轴电流不难发现,ESO+ASMC方法中的电流信号幅度明显要比ESO+SMC方法中的小,相应的系统抖振可明显减弱。由图5可以看出,ESO+ASMC方法中的参数k通过自适应调整收敛于6.4左右,且明显小于ESO+ASMC方法中的直接给定的参数k*=30。
5 结束语
本文提出了一种基于扩张状态观测器的自适应滑模控制方法,用于解决矢量控制下的永磁同步电机调速控制问题。通过扩张状态观测器对影响系统输出的总和扰动的估计,并在此基础上进行自适应滑模控制器的设计,不仅可有效减小输入控制量幅度而且可明显减弱系统抖振。仿真结果表明,所设计的控制器使得永磁同步电机具有良好的转速跟踪性能,并且具有很强的系统参数摄动和负载扰动抑制力。

图2 速度响应曲线Fig.2 Velocity response curve

图3 总和扰动观测Fig.3 Total disturbance observation

图4 q轴电流Fig.4 Current of q axis
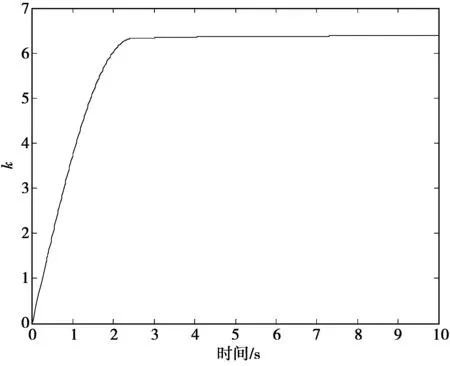
图5 参数自适应曲线Fig.5 Parameter adaptive curve
[1] LI S H, XIA C J, ZHOU X. Disturbance rejection control method for permanent magnet synchronous motor speed-regulation system[J]. Mechatronics, 2012, 22(6): 706-714.
[2] MOHAMED A R I. Design and Implementation of a Robust Current-Control Scheme for a PMSM Vector Drive With a Simple Adaptive Disturbance Observer[J].IEEE Transactions on Industrial Electronics, 2007, 54(4): 1981-1988.
[3] ZHANG C M, LIU H P, CHEN S J. Application of neural networks for permanent magnet synchronous motor direct torque control[J].Journal of Systems Engineering and Electronics, 2008, 19(3): 555-561.
[4] HAN H C, JUNG J W. Takagi-Sugeno fuzzy speed controller design for a permanent magnet synchronous motor[J]. Mechatronics, 2011, 21(8): 1317-1328.
[5] CHOI H H, VU T T, JUNG J W. Digital Implementation of an Adaptive Speed Regulator for a PMSM[J].IEEE Transactions on Power Electronics, 2011, 26(1): 3-8.
[6] CHAI S, WANG L P. Model predictive control of a permanent magnet synchronous motor with experimental validation[J]. Control Engineering Practice, 2013, 21(11): 1584-1593.
[7] TARCZEWSKI T, GRZESIAK L. Constrained State Feedback Speed Control of PMSM Based on Model Predictive Approach[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3867-3875.
[8] 李政,胡广大.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3): 431-436.
LI Zheng, HU Guangda.Sliding-mode Variable Structure Control With Integral Action for Permanent Magnet Synchronous Motor[J].Proceedings of the CSEE, 2014,34(3): 431-436.
[9] 常雪剑,刘凌.永磁同步电机非奇异快速终端可变边界层滑模控制[J].西安交通大学学报,2015,49(6):54-59. CHANG Xuejian, LIU Ling.A Nonsingular Fast Terminal Sliding Mode Controller with Varying Boundary Layers for Permanent Magnet Synchronous Motors[J].Journal of Xi’an Jiaotong University, 2015,49(6): 54-59.
[10] ZHANG D L, KONG T C. A class of second-order sliding mode controller for servo systems[J]. Control Theory and Applications, 2012, 10(2): 268-272.
[11] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京: 国防工业出版社, 2008: 197-206. HAN Jingqing.Active disturbance rejection control technique—the technique for estimating and compensating the uncertainties[M].Beijing: National Defense Industry Press, 2008:197-206.
[12] XUE W C, HUANG Y. On performance analysis of ADRC for a class of MIMO lower triangular nonlinear uncertain systems[J]. ISA Transactions, 2014, 53(4): 955-962.
[13] JIANG T T, HUANG C D, GUO L. Control of uncertain nonlinear systems based on observers and estimators[J]. Automatica, 2015,59: 34-47.
[14] ZHAO Z L,GUO B Z.On active disturbance rejection control for nonlinear systems using time-varying gain[J].European Journal of Control, 2015, 23: 62-70.
[15] HUANG Y, XUE W C. Active disturbance rejection control: Methodology and theoretical analysis[J]. ISA Transactions, 2014,53(4): 963-976.
[16] 康忠健, 陈学允.非线性扩张状态观测器的一种设计方法[J].电机与控制学报,2001,5(3): 199-203. KANG Zhongjian, CHEN Xueyun. A design method of nonlinear extension state observe[J].Electric machines and Control, 2001, 5(3): 199-203.
(编辑:王敏琦)
Adaptive sliding mode controller based on extended state observer for PMSM speed control
GUO Yijun1,2
(1. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310032, P.R.China;2. College of Mechanical and Electrical Engineering, Huangshan University, Huangshan 245041, P.R.China)
In this paper, an adaptive sliding mode control method based on the extended state observer is proposed for permanent magnet synchronous motor speed regulating system with parameter uncertainties and load disturbance. In the presence of the system model parameter uncertainties and load disturbance, the extended state observer is employed to estimate the total disturbance in real time and compensate it in the course of control, thus reducing the influence of the total disturbance on the control precision and improving the dynamic performance of the system. Since the upper bound of the system observation error can not be obtained accurately, the switching control gain of the adaptive sliding mode controller is adjusted by the parameter adaptation law, which can improve the chattering phenomenon of the system effectively and ensure that the system output can track desired signals with high accuracy. Comparing to the traditional PI control method, the simulation results demonstrate that the proposed method achieves smaller overshoot and better tracking accuracy, and has better suppression for parameter uncertainties and load disturbance of the system. Moreover, the proposed method can reduce chattering problem effectively and improve the robustness of the system.
permanent magnet synchronous motor(PMSM); speed regulation; sliding mode control; extended state observer; total disturbance
10.3979/j.issn.1673-825X.2017.01.020
2016-09-12
2016-12-08 通讯作者:郭一军 yjgkmlg@126.com
安徽省高校自然科学研究基金(KJHS2015B11)
Foundation Item:The Scientific Research Foundation of the Education Department of Anhui Province(KJHS2015B11)
TP373
A
1673-825X(2017)01-0137-06

郭一军(1977-),男,浙江金华人,讲师,博士研究生,主要研究方向为非线性系统控制、移动机器人控制技术。E-mail:yjgkmlg@126.com。

