基于乘数交替方向法的系统图像退化恢复方法

魏 勇，孙 波，杨观赐

(1. 河南工学院 计算机科学与技术系，河南 新乡 453003;

2. 贵州大学 现代制造技术教育部重点实验室，贵阳 550003 )

基于乘数交替方向法的系统图像退化恢复方法

魏 勇1，孙 波1，杨观赐2

(1. 河南工学院 计算机科学与技术系，河南 新乡 453003;

2. 贵州大学 现代制造技术教育部重点实验室，贵阳 550003 )

针对一般正则化方法不能有效解决非线性成像和高动态成像的系统退化恢复问题，提出一种非线性图像恢复方法，该方法利用乘数交替方向法解决双边全变差(bilateral total variation,BTV)模型的正则化项不平滑问题。建立包含复原图像的非线性最小二乘数据拟合项和BTV正则化项的目标函数；对目标函数进行优化；构建一套有效的乘数交替方向法(multiplier alternating direction method, MADM)求解提出的模型。利用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性度量(structural similarity index measurement, SSIM)评估图像恢复结果。对于非线性成像系统退化，提出的方法在PSNR和SSIM方面比基于TV(total variation)模型的方法分别提高4.5%和4.1%。对于高动态的成像退化问题，提出的方法获得的恢复图像PSNR值可达61.89 dB，相比其他方法，至少提高了2.9%。此外，该方法的运行时间也至少节省了26%，具有较高的计算效率。

图像恢复；双边全变分；正则化；乘数交替方向法；最小二乘；成像系统退化

0 引 言

图像恢复[1]的目的是对受损坏的图像进行重建和恢复，去除图像的模糊或噪声，保持图像最佳的视觉效果。在科学与工程应用中扮演着重要的角色，例如医学与天文成像、胶卷恢复等[2]。线性成像模型由于其简便性已经被广泛研究并应用，但其准确性和适应性比较差。经验表明，非线性成像模型可以为大量的成像系统提供准确的描述[3-4]，在光化学和光电系统中可以将光强信息非线性地转化成像素密度[3]，如相机响应函数[5]和超分辨率图像[6]等。因此，研究非线性成像系统退化具有非常重要的现实意义。

已经有很多关于图像恢复算法的研究，如偏微分方法[7-10]和混合方法[11-13]，偏微分方法通常以全变差(total variation，TV)及其变形方法为主，这些模型求解过程多使用正则化，混合方法通常将偏微分方法与其他方法或正则化方法组合。文献[7]提出了多种全变差方法，包括一阶全变差、二阶全变差及正则化项变换类型，阐述了利用偏微分方法进行求解的过程。文献[10]的主要贡献在于讨论各种不同形式的局部算子，如TV模型、多通道TV模型、非局部多通道TV模型等，运用快速(split bregman,SP)算法进行运算，并将其应用于彩色纹理图像恢复问题。文献[12]提出一种用于恢复高椒盐噪声图像的方法，即运用灰度空间模糊划分和灰度水平模糊数进行图像恢复，然而，这种技术适用范围较窄，仅对椒盐噪声有效。文献[13]提出使用最小化优化方法进行图像恢复，可解决高动态图像的恢复问题，然而，该方法的每一次迭代过程都需要求解许多病态问题。

本文设计了一种基于双边全变分(bilateral total variation, BTV)[14]的非线性最小二乘图像恢复模型提出了乘数交替方向法(multiplier alternating direction method, MADM)，其创新点在于：将原本涉及非线性最小二乘项和一个BTV正则矩阵的复杂问题转化为以下3个简单问题：独立的极小值问题、近似映像问题和一个结构化线性系统问题，且保证结果的收敛性。相比其他方法，本文方法的主要优势在于能有效解决不平滑的正则化项(即后文的(8)式)。

1 模型描述

对于一个空间不变系统而言，非线性图像降质模型一般可以按照文献[1]中给出的公式描述

(1)

(1)式中:g∈Rm2表示观测图像，实际图像ftrue∈Rm2(对应一张m×m的图像)被非线性分量s(·)、空间不变模糊处理矩阵H∈Rm2×m2和噪声矢量n∈Rm2干扰损坏。当采用周期性边界条件时，模糊处理矩阵是一个循环分块矩阵。当采用诺依曼边界条件时，模糊处理矩阵是一个对称的toeplitz-plus-hankel矩阵[15]，本文仅考虑周期性边界条件。

非线性图像恢复模型虽然更加精确，但计算更加困难。文献[16]提出利用传感器非线性反转方法将有噪声且模糊的图像转换到曝光域，得到乘性噪声存在下的线性最小均方差反卷积滤波器。为了解决非线性最小二乘问题，使用最速下降法，即

(2)

为了进一步考虑非线性最小二乘的高斯-牛顿(gauss newton,GN)算法[17]。基于目标函数(2)在fk处的一阶泰勒级数展开式的非线性近似为

(3)

(3)式中:fk是第k次迭代的结果；Ds是一个对角矩阵，它的对角矢量等于Hfk处的导数s。因此线性最小二乘问题可以通过第(k+1)次迭代结果fk+1得到

(4)

(5)

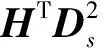
(6)

当μ趋近于0时，H可近似为HT(HHT+μI)-1，每次迭代结果的计算复杂度为O(m2logm)。文献[16]研究了GN方法的收敛性，有趣的是，非线性最小二乘问题(2)的Levenberg-Marquardt方法和通过高斯-牛顿方法得到的Tikhonov正则化的非线性最小二乘问题之间存在如下关系

(7)

(7)式中，μ是正则参数。在原本的最小二乘问题(2)中没有正则项。本文研究基于BTV的非线性最小二乘问题，即

(8)

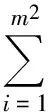
2 乘数交替方向法

由于(8)式中的正则项是不平滑的，现有的处理非线性图像恢复问题的方法不能有效处理公式(8)的模型，故提出了一种有效的乘数交替方向法来解决该问题。MADM法允许将原本涉及非线性最小二乘项和一个BTV正则矩阵的问题转化为一系列简单问题：独立的极小值问题、近似映像问题和一个结构化线性系统问题。经典MADM方法是经典增广拉格朗日方法(augmented Lagrange method,ALM)的实用版本，其中ALM算法用于解决分立结构的线性约束凸问题，在该问题中，目标函数以2个不含耦合变量的独立函数之和形式呈现。MADM方法的理念是将耦合的最小值问题分解为2个更简单的子问题，如此，涉及到的变量即可在交替方向上分别最小化。

重新将模型(8)写成下面的约束优化问题

(9)

使得Hf=z,f=u,f=v,Dif=pi，(9)式中，i=1,2,…,m2，χK1(u)和χK2(v)是指标函数，其定义为

(10)

(11)

约束条件可以表示为

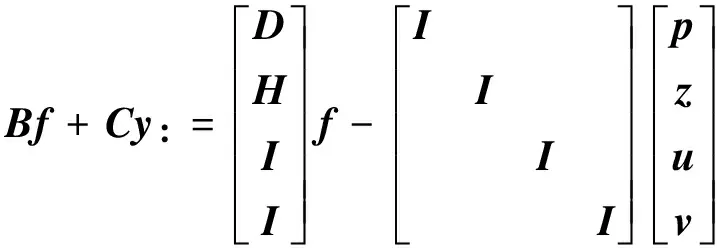
(12)

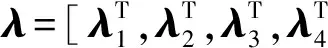
(13)

(13)式中，β>0是为了满足线性约束的惩罚因子。

MADM方法根据f或y计算最小值，然后更新下一组λ值，算法1给出了求解问题(9)的数值算法。

算法1中的步骤1利用二维收缩公式求解p值子问题，步骤3通过向约束集合上投影求解u值和v值子问题，步骤4首先通过快速傅里叶变换求解结构化线性系统，进而求解f值子问题，z值子问题在步骤2中求解。

算法1 求解模型(9)的乘数交替方向法

输入g，f0，λ0，μ，β，a1，a2

输出:fk

当不收敛时，执行以下循环：

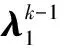
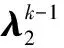
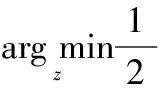
其中，P+(x)=max{x,0}，P-(x)=min{x,0}。

步骤4 给出pk，zk，uk，vk和λk-1，通过求解下面的线性系统更新fk值

步骤5 更新λk

λk=λk-1+β(Bfk+Cyk)

循环结束

3 实验结果

所有仿真实验均在Windows 7操作系统上进行，平台为MATLAB(R2010a)，计算机配置为：英特尔酷睿2双核处理器、2.66 GHz主频、4 GB内存。

3.1 评价函数

本文使用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性指标(structural similarity index measurement, SSIM)评估图像恢复结果。其中PSNR可以表征图像高频成分损失情况，PSNR值越高，表明高频分量损失越小。SSIM用于衡量2幅图像的相似程度，SSIM非常符合人眼对图像品质的判断标准，取值在0和1之间。PSNR的定义为

(14)

(15)

(15)式中:g(i，j)代表原始图像每个元素灰度值；经图像恢复后，(i,j)位置对应的像素灰度值为G(i，j)，处理前后图像大小不变，宽高分别为W，H。通过提供复原图像的PSNR值来选择他们相应的正则化参数。根据连续解的相对变化是否低于给定容差来决定数值算法的停止条件。

SSIM定义为

(16)

(16)式中，ux及uy、σx及σy分别为图像x，y的平均值和标准差，σxy为x，y的共变异数，C1，C2，C3均为常数(本文范围内这些常数均取1)。一般情况下，取图像局部窗口，遍历整个图像，直到整个图像的SSIM计算完毕，将所得SSIM值平均，并将其结果作为x，y图像的结构相似性指标。

3.2 非线性成像退化

将几种处理非线性成像系统退化的恢复方法进行比较：非线性最小二乘模型(nonlinear least square,NLS)、基于全变分的非线性最小二乘模型(total variation-nonlinear least squares，TVNLS)和基于双边全变分的非线性最小二乘模型(bilateral total variation-nonlinear least squares，BTVNLS)。NLS模型通过GN方法求解，TVNLS和BTVNLS则通过MADM方法求解。测试图像是图1a。停止容差设置为10-5，除另有说明外，初始猜测均设为逆像s-1(g)(s-1表示分量形式的逆非线性)。算法1的内Newton迭代次数设为5。

图1 原图Fig.1 Original pictures

在第1个实验中，评估BTVNLS模型恢复非线性降质图像的表现，在光化学系统中，假设光密度与入射光强是对数关系[1]，本文在具有线性响应的区域使用对数函数。在光电系统中，入射光强和光电传感器的输出满足幂律关系[1]。光电系统函数的变量上升为指数形式。本文测试一类非线性函数，即自然对数函数ln(x)。

当考虑自然对数非线性函数时，利用NLS模型、TVNLS模型和BTVNLS模型进行图像恢复，结果如图2所示。相应的PSNR值、SSIM值、迭代次数、CPU计算时间和其他参数分别为NLS(PSNR：26.95 dB，SSIM：0.8036，迭代次数：1526，计算时间：42 s，μ=5×10-2)，TVNLS(PSNR：28.68 dB，SSIM：0.8848，迭代次数：980，计算时间：68 s，μ=5×10-7，β=10-6)，BTVNLS(PSNR：29.35 dB，SSIM：0.9148，迭代次数：998，计算时间：70 s，μ=5×10-7，β=10-6)，所以，BTVNLS模型的PSNR值和SSIM值比TVNLS模型和NLS模型的更优，相比NLS模型，BTVNLS的PSNR和SSIM值分别改进了约6.0%和9.2%，相比TVNLS模型，约提高了4.5%和4.1%。图3显示了对图2a中放大的“支架”部分进行不同模型恢复的图像对比，进一步说明了使用BTVNLS模型可以显著提高恢复图像的质量。另一方面，图4分别给出了NLS模型、TVNLS模型和BTVNLS模型在不同迭代次数下的PSNR结果。可以发现，迭代次数较少时，TVNLS模型的PSNR值增长速度低于NLS模型。但是，当迭代次数较大时，NLS模型的PSNR值没有继续增加，而TVNLS模型的PSNR仍继续上升。TVNLS模型的PSNR与BTVNLS模型相当，但整体上低于BTVNLS。

图2 在使用非线性自然对数函数降质时，不同模型恢复的图像对比Fig.2 Restored image comprison by different model with degraded image using a nonlinear function of the natural logarithm.

3.3 高动态的成像退化

低动态范围(low dynamic range, LDR)成像对高动态范围(high dynamic range, HDR)辐亮度呈非线性响应，非线性响应可以写成

(15)

(15)式中：r为真实的HDR辐亮度，g为LDR观测图像，s为相机响应函数，表示HDR辐亮度到LDR观测图像的映射。文献[16]给出了封闭式的非线性函数

(16)

(16)式中，c1，c2是相机设置中的2个正常数，采用BTVNLS模型从含噪声的LDR观测图像g中恢复真实的HDR辐亮度r。BTVNLS模型利用MADM法求解。这里测试数个正则化参数μ=i×10j(i=1和5，j=3，4，5和6)。

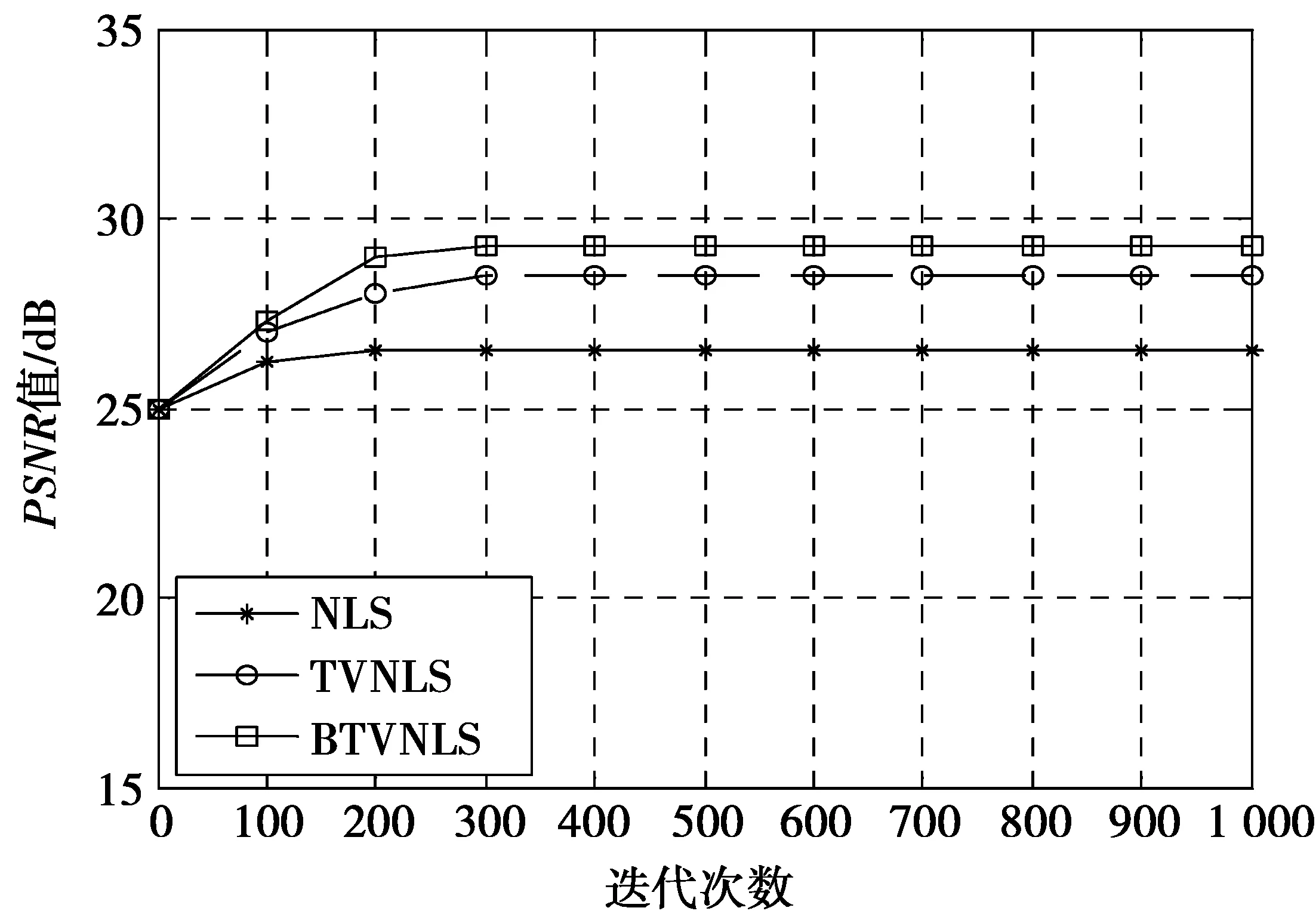
图4 非线性自然对数降质处理下，不同模型的迭代次数对PSNR值的影响Fig.4 Numbers of iterations vs PSNR value for different model, in the processing of degradation by nonlinear nature log

实验首先测试了3张720×576的HDR图像。第1张HDR图像“办公室”的值范围在0.992 9到5 612.3。第2张HDR图像“路灯”的取值范围则在13.453 4到35 013，是夜间拍摄的彩色图像，第3张HDR图像“车”的取值范围则在12.134 9到8 600.9，也是夜间拍摄的彩色图像。常数C2的值设置为1，常数C1取值需保证s(r)的值在0到1。

在MADM法中，Newton迭代次数设为5、初始猜测值为逆像。文献[13]提出一种解决上述HDR辐亮度的恢复方法，即最小化优化(majorized minimum，MM)。利用加权最小二乘技术来处理不平滑的TV项，利用线性化技术来处理非线性最小二乘数据拟合项[13]。然而，该方法主要的计算障碍是在每一次迭代过程中都需要求解许多病态系统，可采用文献[16]的共轭梯度法来解决病态线性系统。文献[10]提出非局部TV模型，采用Split Bregman进行运算，各方法的迭代停止容差设为3×10-5。

图5给出不同方法的恢复结果，图5a是含噪声的LDR观察影像，图5b是非局部TV模型，图5c和图5d是从HDR复原图像中得到的LDR色调映射图像，分别利用MM法和MADM法计算获得。非局部TV方法和MM方法的惩罚因子都设为μ=10-4，MADM法的参数设置为：μ=10-4，β=4×10-4。从视觉角度看，使用MADM法恢复的HDR图像比MM法更佳。从色调映射图像看，MADM法的效果比MM方法和非局部TV方法更好。图6和图7是夜间拍摄的图像，为彩色图像，参数设置均与图5相同，从图6和图7可以看出，本文方法的图像恢复效果同样优于其他几种方法。

图5 各个方法的恢复结果Fig.5 Restoration results of some methods

图6 夜间的HDR图像恢复效果(a)Fig.6 Restoration results of high dynamic range images in the night(a)

图7 夜间的HDR图像恢复效果(b)Fig.7 Restoration results of high dynamic range images in the night(b)

这部分实验所用图像为50多幅相机拍摄的高动态图像，表1所示为各方法的恢复图像平均PSNR值以及平均计算时间比较，从表1可以看出，在PSNR方面本文方法略高于其他方法，PSNR值提高了至少2.9%，而运行时间也明显少于其他方法，减少了至少26%。充分表明了MADM在处理正则化模型方面的优势。(注：高动态图像的PSNR值会明显高于其他一般图像的PSNR值，故表1的PSNR值普遍高于表1中的结果)

表1 各个方法的恢复图像平均PSNR以及平均计算时间

3.4 参数设置的影响

本节讨论BTVNLS模型中的参数设置，即迭代次数、惩罚因子和MADM方法的初始猜测值。

1)迭代次数：因为从图4可以看出，即使进行更多次迭代，PSNR值也没有太大提升，故没必要为了获得具有较高PSNR值的复原图像而进行多次迭代。

2)惩罚因子：图8为恢复图像在不同惩罚因子下所需CPU计算时间的关系图，从图8中可以看出，惩罚因子的值的确可以影响BTVNLS模型。对自然对数非线性降质图像来说最佳的惩罚因子为β=1×10-6，即本文模型需要一个较小的惩罚因子。

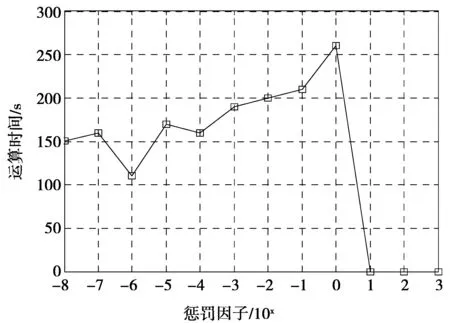
图8 惩罚因子与运算时间关系图Fig.8 Chat of penalty factor and the operational time

3)初始猜测值：MADM法中使用的初始猜测值对求解BTVNLS模型影响较大。利用MADM法求解TVNLS和BTVNLS模型，MADM法的预设值包括白场图像、随机图像、观测图像g=s(r)和逆像s-1(r)。实验采用逆像作为初始猜测值，发现仅需进行5次迭代即可获得较好的恢复结果。但是，当实验采用其他初始猜测值(如白场图像、随机图像、观测图像)时，需要经过更多次迭代才能得到与前者相当的恢复图像。

4 总结与展望

本文提出了一种有效的乘数交替方向法，通过求解非线性最小二乘数据拟合项和BTV正则项，处理非线性成像系统退化和高动态成像退化的图像恢复问题。实验部分给出了数值实例，此外，还研究了一些参数的影响。结果表明，本文方法具有较好的恢复效果和较高的计算效率。

本文方法中，由于正则化的计算复杂度依然较高，未来将研究这些运算之间是否有并行处理的可能性，尝试进一步提升运行速度。

[1] RAFAEL C G, RICHARD E W.数字图像处理[M].3版.北京：电子工业出版社，2011. RAFAEL C G, RICHARD E W. Digital Image Processing[M]. 3ed. Beijing ：Electronic Industry Press.2011.

[2] 张蕴婉, 刘洋, 黄静,等. 正常剂量扫描导引的低剂量心血管CT造影图像恢复[J]. 南方医科大学学报, 2013, 23(9): 1299-1303. ZHANG Yunwan, LIU Yang, HUANG Jing, et al. Low-dose CT angiography image restoration using normal dose scan-induced non-local means algorithm[J]. Journal of Southern Medical University, 2013, 23(9): 1299-1303.

[3] GUNTURK B K, LI X. Image restoration: fundamentals and advances[M]// Image restoration: fundamentals and advances. CRC Press, 2013.

[4] 严辉. 强非线性薄膜的光学超分辨效应与超分辨成像应用探索研究[D]. 北京: 中国科学院大学, 2014. YAN Hui. Strong nonlinear optical film super-resolution effect and applications of super-resolution imaging[D].Beijing:University of Chinese Academy of Sciences,2014.[5] KIM S,TAI Y W,KIM S,et al.Matsushita,Nonlinear camera response functions and image deblurring[C]∥25thIEEE Conference on Computer Vision and Pattern Recognition.Rhode Island,USA:IEEE,2012:25-32.

[6] GUNTURK B K. Handling exposure time in multi-frame image restoration[C]// 2005 IEEE International Conference on Acoustics, Speech, and Signal Processing. Philadelphisa, Pennsylvania, USA: IEEE, 2005: 865-868.

[7] 史宝丽. 几类全变差型图像恢复模型研究[D]. 长沙：湖南大学, 2012. SHI Baoli.Research of several models of total variation image restoration[D].Changsha:Hunan University,2012.

[8] 胡辽林, 王斌, 薛瑞洋,等. 基于可分离全变差模型的图像去噪[J]. 光子学报, 2014, 37(9)1207-1213. HU Liaolin, WANG Bin, XUE Ruiyang, et al. Image De-noising Based on Seqerable Total Variation Model[J]. Acta Photonica Sincia, 2014, 37(9): 1207-1213.

[9] TAKEDA H, FARSIU S, MILANFAR P. Deblurring using regularized locally adaptive kernel regression[J]. IEEE Transactions on Image Processing. 2008, 17(4): 550-563.

[10] 端金鸣, 潘振宽, 台雪成. 彩色纹理图像恢复的非局部TV模型[J]. 中国图象图形学报, 2013, 18(7): 753-760. DUAN Jinming, PAN Zhenkuan, TAI Xuecheng. Non-Local TV models for restoration of color texture images[J]. Journal of Image and Graphics, 2013, 18(7): 753-760.

[11] 肖创柏, 赵宏宇, 禹晶,等. 基于WLS的雾天交通图像恢复方法[J]. 红外与激光工程, 2015, 34(3): 1080-1084. XIAO Chuangbai, ZHAO Hongyu, YU Jing, et al. Traffic image defogging method based on WLS[J]. Infrared and Laser Engineering, 2015, 34(3): 1080-1084.

[12] 王贵君, 杨永强. 基于高概率椒盐噪声的模糊滤波器在图像恢复中的算法设计[J]. 电子学报, 2015, 37(1): 986-991. WANG Guijun, YANG Yongqiang. Algorithm design of fuzzy filter based on salt-and-pepper noise with high probability in image restoration[J]. Journal of Electronics, 2015, 37(1): 986-991.

[13] LV W, LIU W, WEI Z, et al. Design of high dynamic range imaging optical system based on DMD[J]. Infrared & Laser Engineering, 2014, 43(4): 1167-1171.

[14] 邱宇. 基于双边滤波的图像去噪及锐化技术研究[D]. 重庆：重庆大学, 2011. QIU Yu. Research of image de-noising and sharpening technology based on bilateral filtering[D]. Chongqing: Chongqing University, 2011.

[15] 吴化璋, 陈公宁. 关于无限广义块Toeplitz+Hankel矩阵的求逆[J]. 北京师范大学学报：自然科学版, 2001, 37(1): 10-15. WU Huazhang, CHEN Gongning. On the inverses of infinite gerneralized block toeplitz-plus-hankel matrices[J]. Journal of Beijing Normal University: Natural Science, 2001, 37(1): 10-15.

[16] 陈忠, 黄惠. 求解非线性最小二乘问题的迭代法[J]. 武汉大学学报:理学版, 2003, 49(1): 14-16. CHEN Zhong, HUANG Hui. Iterative method for solving nonlinear least-squares problems[J]. Journal of Wuhan University：Natural Science Edition,2003,49(1):14-16.

[17] ZERVAKIS M E， VENETSANOPOULOS A N. Convergence properties of Gauss-Newton iterative algorithms in nonlinear image restoration[J]. Multidimensional Syst. Signal Process. 1992, 2(3): 287-318.

(编辑：张 诚)

An image restoration method for degradation of imaging system based on multipliers alternating direction method

WEI Yong1, SUN Bo1, YANG Guanci2

(1. Department of Computer Science and Technology, Henan Institute of Technology, Xinxiang 453003, P.R. China; 2. Key Laboratory of Advanced Manufacturing Technology of Ministry of Education, Guizhou University, Guiyang 550003, P.R.China)

As common regularization cannot solve image restoration effectively in the cases of nonlinear imaging and high dynamic imaging, a nonlinear image restoration method is proposed, and in which multiplier alternating direction method is used to solve the non-smooth regularization problem in bilateral total variation (BTV) model. Firstly, the objective function that includes term of BTV regularization and term of nonlinear least squares fitting is created. Then, the objective function is optimized. Finally, an effective multiplier alternating direction method (MADM) is proposed to solve the proposed model. Peak signal to noise ratio (PSNR) and structural similarity index metric (SSIM) are applied to assessing the results of image restoration. For degradation of nonlinear imaging system, PSNR and SSIM of the proposed method is 4.5% and 4.1% more than that of other methods based on TV model respectively. For degradation of high dynamic imaging system, PSNR of the restored image can get 61.89 dB in the proposed method, which is 2.9% more than that of other algorithms. Meanwhile, the running time is reduced by at least 26%, with efficiency computation.

image restoration; bilateral total variation; regularization; multiplier alternating direction; least squares; imaging system degradation

10.3979/j.issn.1673-825X.2017.01.017

2015-09-20

2016-06-02 通讯作者：魏 勇 weiyonghnxx@126.com

河南省教育厅科学技术研究重点项目(13A520221，14A520045)；河南省高等学校重点科研项目(16B520010，16A520084，16A520083)；贵州省重大基础研究项目(黔科合JZ字[2014]2001号)

Foundation Items：The Key Project of Science and Technology Research From Education Department in Henan Province(13A520221, 14A520045); The Key Scientific Research Projects of Henan Province(16B520010，16A520084，16A520083); The Major Fundamental Research Program in Guizhou Province (Guizhou branch in JZ words [2014]2001)

TP391

A

1673-825X(2017)01-0113-08

魏 勇(1982-)，男(汉)，河南卫辉人，讲师，硕士，研究领域：多媒体技术、软件工程等。E-mail：weiyonghnxx@126.com。 孙 波(1983-)，男，讲师，硕士，研究领域：图像处理、智能算法等。 杨观赐(1983-)，男，博士，副教授，硕士生导师，IEEE会员、CCF会员，研究领域：图像处理、计算智能与智能系统等。