高中数学导学案设计与使用问题的研究

罗柏生

摘 要：导学案的出现改变了高中传统数学教学模式，也给教师的教学提出了更高要求。目前，在高中数学教学中，导学案的使用存在一些问题，主要是学生主体性没有得到体现，学案教案化现象严重；内容的选择和使用有错位；设计不合理，忽视了学生的主体地位；问题设计过于随意，内在逻辑性较差等问题。为了突出导学案教学工具的特性，教师在导学案的使用和设计中要进一步研究学生，突出学生的主体地位；让学生探索知识的生成过程；设计的问题要有内在联系，这样才能有助于教学效果的提高。

关键词：高中数学 导学案 设计与使用 问题

随着新课程改革理念的大力推行，学生在数学学习过程中不仅要学习硬性知识和模仿练习，还要发展自主探索能力、合作交流能力和阅读自学能力。为此，很多新型的教育理念和教育方法被广泛应用于教学实践中，而导学案作为一种行之有效的教学手段，顺应了新课程改革的要求，已被应用于高中数学教学之中。

在现实教学当中，很多教师对于导学案的实施只是略懂皮毛，因此做了一些不科学的导学案，误导了对新课程的探索。由于学生是教学的主体，一切教学活动都是围绕他们而展开的。通过合理的导学案教学模式，学生对数学学习的积极性有了明显提升，为培养学生的自主学习能力和自主创新能力提供了基础。如果在导学案设计与实施过程中，不遵循科学的规律，盲目使用导学案，不仅不会提高学生的学习效率，反而会使学生失去学习数学的兴趣，阻碍学生的发展。

一、导学案在高中数学教学中存在的问题

1.学生主体性没有得到体现，学案教案化现象严重

以《函数的单调性》导学案的设计为例，在新知导读部分，教师一般会设计很多问题，学生只是被动地完成教师布置的任务。例如，第一部分，借助图象，直观感知。教师可要求学生：“观察函数y=x+1，y=-x+1和y=x2的图象特点，并描述变量与自变量之间的关系，总结出增函数与减函数的特征。”第二部分，训练抽象思维，形成相关概念。接下来教师可继续提问：“如何运用解析式y=x2，证明它在[0，+∞）上为增函数？怎样利用数学概念的形式来定义增函数和减函数？在学习函数的单调性时，有哪些事项需要注意？”这一系列的问题都需要学生通过教材中的知识来解决，换句话说如果学生不看书是绝对不会解决这些问题的。这样一来就会造成学生为完成“任务”而照搬教材内容，出现不求甚解的状况。函数的单调性是高中阶段数学概念中的核心概念，学生要通过教师的引导来充分理解定义，而不是被动地接收那些浅显而孤立的“知识点”。

2.内容的选择和使用有错位

通过对大量导学案的汇总和整理，我们会发现，这些导学案除了在设计形式上相似以外，在内容的实质上跟教案是一回事。导学案的设计初衷是一切为了围绕学生的“学”展开，强调学生的“学”，但在很多教师手中，导学案却变成了另一種形式的教案：如将教案中的教学目标直接转为导学案中的学习目标；教学重点和难点直接转为学习重点和难点；直接将教材上的定义以填空题形式出现在导学案上（见表1）。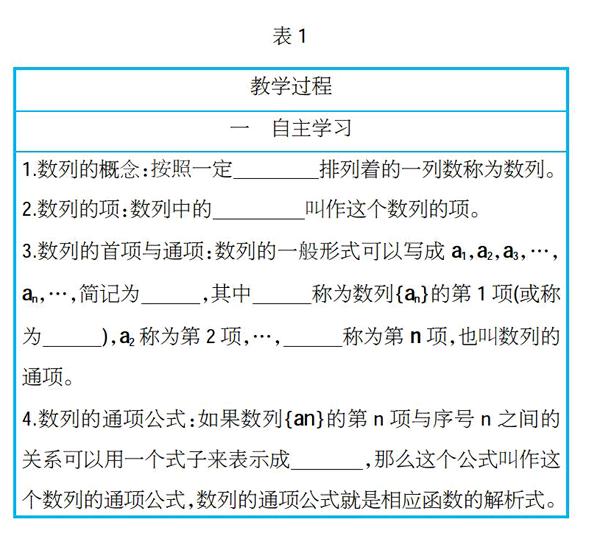

有些教师直接把导学案做成了练习册，导学案上的内容大都是课后练习题和辅导教材。将导学案设计中的知识问题化转化成了知识习题化，使导学案失去了原有的导学功能。还有些教师为了使导学案的内容更加丰富，引入的知识和习题超出了课程标准要求，使学生的学习偏离了主线。例如，很多教师在教学《等差数列》第一课时“自主学习”栏目时，就引入了公式，在第一课时就让学生接触这一知识会让学生感到很有难度，而且这也不是第一课时的教学重点。

3.设计不合理，忽视了学生的主体地位

导学案的主要功能就是引导学生自主学习，要突出学生学习的主体性和导学案导学的功能。而有些教师在设计导学案时，只是流于形式，根本不考虑学生的主体地位。以《平面向量的实际背景和基本概念》这一部分的导学案设计为例。

在“新知导学”部分设计了大量问题：（1）向量的概念。什么叫作向量？向量与数量之间有什么区别和联系？（2）向量的表示方法。向量有哪些表示方法？如何理解向量的方向？什么叫作单位向量？（3）平行向量和相等向量。平行向量和相等向量的定义是什么？它们之间有什么关系？

作为向量内容学习的第一课时，教师要引起学生的兴趣，提高学生“做”数学的能力，而不是仅学习这几个浅显的向量定义。由于教师在设计本章节的导学案时，没有充分阅读教材，忽略了本章节的“向量物理背景”部分和“阅读与思考”部分的重要性。当学生拿到导学案后，看到这些枯燥的问题时，都忙于从教材上照搬答案，根本体现不出“导学”的作用。教材课后练习题第一题就明确提出了“要考查学生的动手能力，要求学生利用直尺和圆规画出要求的向量”，而该导学案却没有体现这一点。

4.问题设计过于随意，内在逻辑性较差

通过对导学案的观察和对学生的访谈发现：第一，导学案设计的问题大都是教材上直观的概念性问题，难以引起学生的兴趣。第二，设计的一些问题过于死板，不利于学生发散思维的训练和创新思维的培养。第三，设计的问题太过零碎，不利于学生系统地掌握知识。第四，设计的问题难度没有层次性和选择性，有的学生认为很难，不想做；有的学生认为太简单，没有必要做。如《复数代数形式的乘除运算》导学案的设计：

新知导读部分：（1）复数的乘法运算。问题一，设z1=a+bi，z2=c+di（a，b，c，d∈R），为任意两个复数，那么z1·z2= 。（点拨：两个复数相乘跟两个多项式相乘相同，即把结果中i2转换成 ，再将它们的实数部分和虚数部分分别合并，得出的结果仍然是个复数。）问题二，设计问题，检验复数乘法的运算规律。（2）复数的除法运算。什么叫作共轭复数？它们的乘积是虚数还是实数？复数的除法运算规则是什么？请列出题目并加以证明。

从这部分导学案的设计中我们可以看出：既有定理的引出，又有定理的验证，线性地开展了复数运算部分的导学，但没有设计出促进学生深入思考的问题，没有起到扩展学生思维的作用。这样的导学案不利于学生形成网络化的知识体系，也不利于学生后期对知识的运用。

二、高中数学导学案设计与使用建议

1.研究学生，突出学生主体地位

第一，在设计和编写导学案前期，教师要做好充分的学情分析，通过对学生的了解，有针对性地设计教学策略。同时，教师还要熟悉教材内容，了解知识之间的相互联系，明确编写本次导学案的主要目的，以此设定导学案的框架，并根据学生的实际情况，考虑分层教学。教师可以根据学生的能力，设计相关的教学问题情境。如为了能使学生对函数单调性的认识从图象上升到数学符号，教师可以这样设计问题：通过观察函数y=x+■（x>0）的图象，说一说它的递增区间和递减区间。

这道题的难点就在于难以确定这两个区间的分界点，要让学生知道仅仅依靠图象是难以确定函数的单调区间的，只有数学符号才能清楚地体现函数的相关信息，从而引领学生将函数单调性的研究从函数图象过渡到函数解析式。

2.让学生探索知识的生成过程

导学案在设计与编写中要本着主体性、探究性、引导性、参与性和实用性的原则，根据教师和学生的实际情况而设计，以简单实用为根本。导学案的设计内容应包括学习目标、学习重点难点、学习方法指导、旧知复习和情境引入、新科探究、课堂检测、学习小结等方面，最后还可以留出一部分內容作为学生学习反思使用。例如，在“三角函数的诱导公式”一节内容的学习中，通过逐层递进，逐步分析的方法，即角间关系—对称关系—坐标关系—三角函数值间关系的研究路线来建立知识框架，让学生体验整个知识系统的构建过程，学会对知识的探索，促进知识体系的形成。

3.设计的问题要有内在联系

数学思维的培养需要数学问题作铺垫，系统的数学问题能够帮助学生形成系统的知识体系，加深学生对相关概念中关键词的理解，因此，在设计数学问题时要注重设计题目之间的联系性。例如，在“函数的单调性”一节中设计的问题是：问题一，对于函数f（x），在区间[-1，1]上取两点a=-1，b=1，当a

三、结语

导学案是新课程改革实施背景下产生的教学方式，它能够有效提高学生的自主学习能力和创新能力，但不科学地使用会阻碍教学功能的发挥。因此，在高中数学教学中关注导学案的设计与使用对于提高数学教学效果有重要意义。

参考文献：

[1]杨鹏展.高中数学“导学案”使用中出现的问题及对策[J].教学论坛，2011（5）.

[2]韩立福.论学案教学的利弊及改进建议[J].教学与管理，2012（10）.

[3]顾福军.警惕“学案”导学陷入“低效”的漩涡[J].数理化学习.2012（1）.

[4]王俊亮.导学案在高中数学命题教学中的应用研究[D].济南：山东师范大学，2011.