含裂纹的压力容器疲劳寿命仿真分析

宫羽丽，牛庆良

设备与自控

含裂纹的压力容器疲劳寿命仿真分析

宫羽丽1，牛庆良2

(1.中海油石化工程有限公司，山东 济南 250000；2.华电电力科学研究院山东分院，山东 济南 250000)

针对裂纹对压力容器疲劳寿命的影响，应用断裂力学理论将存在初始裂纹的压力容器进行应力强度因子计算，采用Paris理论对裂纹扩展速率进行描述，应用ANSYS workbench仿真计算含裂纹的压力容器的应力强度因子和应力分布。根据计算结果进行疲劳寿命分析，研究裂纹对应力分布和疲劳寿命的影响，为含裂纹压力容器的设计提供一定的参考。

压力容器；应力强度因子；疲劳寿命

压力容器出现的事故大多与容器结构中存在的缺陷或裂纹有关，对裂纹扩展规律进行系统深入的研究具有重要的理论价值和现实工程意义。当前，压力容器设计通常采用疲劳设计曲线进行，如美国的ASME Ⅲ、ASME Ⅷ-2[1]、中国的《钢制压力容器-分析设计标准》(JB 4732-2005)[2]等。根据试验得到材料疲劳失效的平均寿命曲线，再按虚拟应力幅和循环次数设定安全系数，取二者中平均寿命较短的作为分析材料的疲劳设计曲线。Langer的研究成果以无缺陷光滑试样的疲劳试验为基础，包括裂纹萌生和扩展至断裂的阶段，忽略了初始裂纹的影响。

在对压力容器疲劳寿命预测和裂纹形貌的确定上，许多学者采用实验与理论相结合的方法进行研究。Shih和Chen根据应力强度因子和含裂纹的转轴之间的关系，建立疲劳寿命及裂纹转轴分析的模型[3]。吴志学应用自由数值模拟方法对表面裂纹进行了深入分析，对裂纹形貌及其裂纹沿SIF分布进行研究[4]。Toribio等采用应力强度因子与Paris公式相结合的方式对拉伸载荷下的棒料试样进行裂纹扩展模拟，改变初始裂纹的横纵比来模拟不同的初始裂纹形貌[5]。

作者针对裂纹对压力容器疲劳寿命的影响，应用ANSYS workbench仿真计算含裂纹的压力容器的应力强度因子和疲劳寿命，分析裂纹对应力和疲劳寿命分布的影响，为含裂纹的压力容器的设计提供一定的参考。

1 裂纹对材料强度的影响

如果材料生产中存在缺陷或者加工中产生划痕及焊缝缺陷等，则给压力容器的寿命及安全带来极大影响。在弹塑性条件下，当裂纹尖端的应力强度因子K达到该种材料的断裂韧度KIC时，裂纹就会失稳扩展，如式(1)所示。影响断裂韧度的因素有化学成分、组织结构以及外界环境[6]。

K≥KIC(1)

1.1 椭圆裂纹应力强度因子

假定压力容器中圆筒形壳体表面存在裂纹，裂纹与轴向应力垂直。由于裂纹的尺寸远小于结构的曲率半径，将此情况等效为无穷远处受到均匀纵向应力σx和横向应力σy的存在中心裂纹的无限大板模型。半椭圆形裂纹简化模型如图1所示。

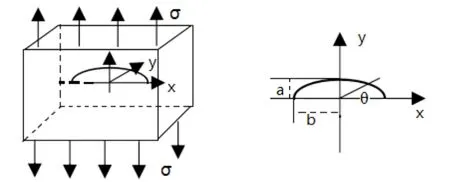
图1 半椭圆裂纹简化模型

其应力强度因子[7]表达式为：

对于内部椭圆裂纹，其应力强度因子表达式为：

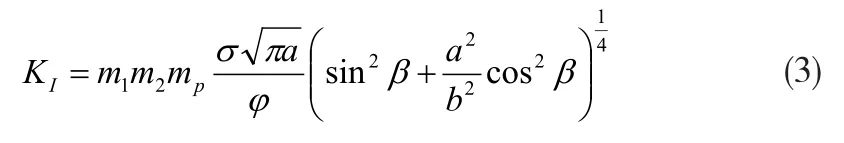
式中，m1为前自由表面增大因子，m2为前自由表面增大因子，mp为塑性区增大因子，φ为第2类椭圆积分。

1.2 穿透裂纹应力强度因子

对于存在穿透裂纹的压力容器，将其等效为受均匀荷载含中心穿透裂纹的无限大板模型，中心长为2α，均匀拉应力σ（垂直于裂纹平面）（图2），其应力强度因子为[8]：

2 存在裂纹的压力容器疲劳寿命

构件的疲劳寿命N是疲劳裂纹萌生寿命NI与裂纹扩展寿命Np之和：

N =NI+Np(5)

其中，Np所占的比例高达 90%以上，这一阶段在构件疲劳寿命中起决定作用[9]。裂纹扩展速率决定了构件的疲劳寿命，应用Paris公式描述裂纹扩展速率[10]：

式中，dα/dN为疲劳裂纹扩展速率；ΔK为每一次循环中的应力强度因子变化幅值；C为帕里斯公式系数；n为帕里斯公式指数。α0为裂纹初始长度，αc为裂纹临界尺寸。

应用Miner线性累积损伤理论[11]，当裂纹从初始尺寸α0扩展到αc时，对式(6)积分得到裂纹扩展寿命Np：

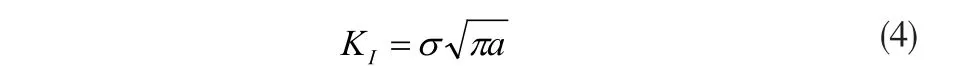
图2 中心穿透裂纹简化模型

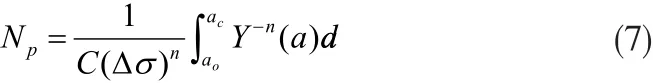
对于半椭圆裂纹，有：

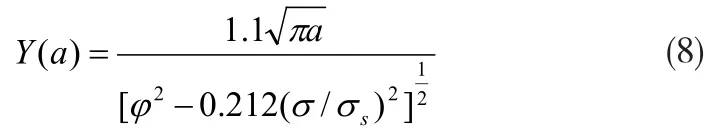
将式(8)代入式(7)得：

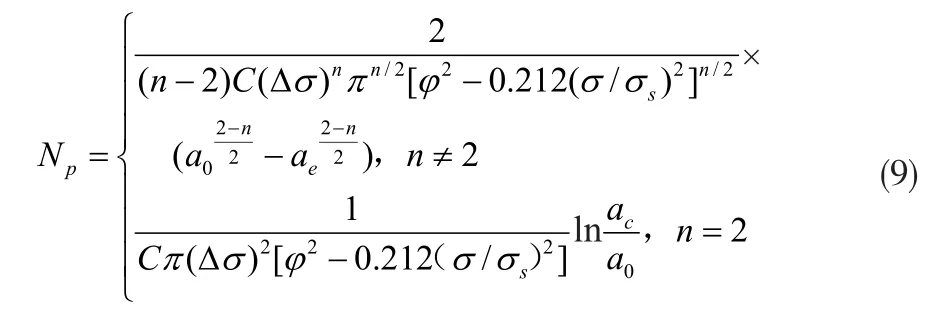
对于穿透裂纹，有：

将式(10)代入式(7)得：

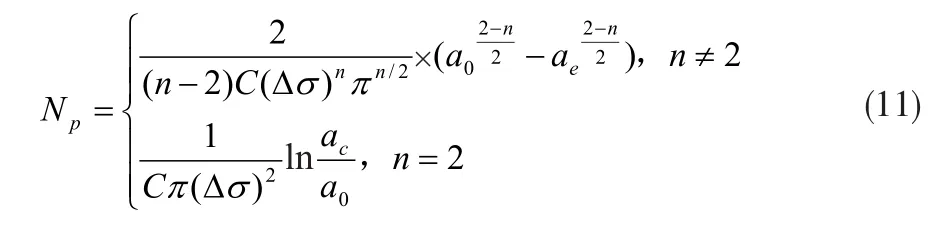
3 存在裂纹的压力容器疲劳寿命仿真计算

有限元法是将变分原理和有限差分法结合的一种数值方法，将连续的求解域离散为有限单元的组合体，用在每个单元内假设的近似函数来分片地表示求解域上待求的未知场函数[12]。边界元法作为计算裂纹尖端应力强度因子的基本理论，可以计算在均匀内压作用下不同厚壁筒表面裂纹的应力强度因子[13]。

3.1 压力容器模型

在ANSYS workbench 的Geometry模块中，建立1/4压力容器圆筒形壳体模型如图3所示。材料为Q345R，尺寸D=1000mm，厚度10mm，屈服强度345MPa，抗拉强度为580MPa，弹性模量E=209GPa，断裂韧度48MPa·mm0.5（空冷，常温），泊松比v=0.3。

图3 1/4压力容器模型

3.2 应力强度因子计算

设定材料参数、载荷及约束，在压力容器圆筒形壳体表面插入半椭圆形裂纹，各参数设置如图4所示。长半轴为12mm，短半轴为6mm。选择四面体单元划分网格如图5所示。在Tool下选择Fracture模块计算裂纹应力强度因子，结果如图6所示。

图4 裂纹参数

图5 裂纹网格划分

图6 应力强度因子分布

由图6可知，裂纹前缘应力强度因子最大，依次向两端递减，最大值278MPa·mm0.5，最小值153MPa·mm0.5，均大于材料断裂韧度值48MPa·mm0.5，说明裂纹将继续扩展，将加剧缩短压力容器的疲劳寿命。为观察裂纹形貌对应力强度因子的影响，改变短轴的长度，使短长轴比例为0.5、0.6、0.7、0.8、0.9、1.0，依次计算出不同比例下沿裂纹前缘的应力强度因子如表1所示。结果表明随着短长轴的比值增大，应力强度因子也增大。

表1 不同比例下应力强度因子值 /MPa·mm0.5

3.3 等效应力分布

在Static Structural模块中对边缘截面选择Fixed Support约束，内表面选择Pressure载荷，垂直于内表面，大小为3MPa。等效应力计算结果如图 7所示。

图7 等效应力分布

由图7可知，裂纹尖端处最大应力是362MPa，大于材料的屈服强度345MPa，该处会发生失效变形。除裂纹之外，压力容器上的应力均小于282MPa，满足材料屈服强度。裂纹对等效应力分布影响显著，说明忽略初始裂纹的设计会大大影响压力容器的使用寿命。

3.4 疲劳寿命计算

考虑裂纹对疲劳寿命的影响，为压力容器的寿命评估提供参考，在Fatigue Tool中进行疲劳寿命计算，工作参数如表2所示。疲劳寿命分布如图8所示，安全系数分布如图9所示。

表2 压力容器工作参数

图8 疲劳寿命分布

图9 安全系数分布

由图8、9可知，裂纹处存在最小疲劳寿命，即1.08×105次，小于工作循环次数 9×105次，另安全系数为0.6，故裂纹处不符合设计寿命的要求。裂纹以外疲劳寿命均大于9.05×105次，安全系数大于3，满足压力容器寿命设计要求。

4 结论

通过对含裂纹压力容器的应力强度因子和疲劳寿命的研究，给出了基于 ANSYS workbench 的裂纹疲劳分析方法。结合有限元建模方法，能够快速有效地对含初始裂纹的压力容器的疲劳寿命进行仿真分析。实例表明，裂纹对等效应力分布影响显著，初始裂纹的存在会大大影响压力容器的使用寿命。

[1] 郭东，等.存在裂纹的压力容器疲劳断裂分析[J].建筑科学与工程学报，2007，24(3)：87-90.

[2] 压力容器实用技术丛书编写委员会.压力容器设计知识[M].北京：化学工业出版社，2005.

[3] Shih Y.S., Chen J.J. Analysis of fatigue crack growth on a cracked shaft [J]. International Journal of Fatigue, 1997, 19(6): 477-485.

[4] 吴志学.表面裂纹疲劳扩展的数值模拟[J].应用力学学报，2006，23(4)：563-568.

[5] Toribio J., Matos J.C., Gonzalez B. Numerical modelling of crack profile evolution for surface flaws in round bars under tensile loading[J]. Engineering Failure Analysis, 2009, 16: 618-630.

[6] 王磊，等.压力容器材料韧性断裂细观力学分析与测试[J].石油化工设备，2007，36(1)：59-93.

[7] 于骁中.岩石和混凝土断裂力学[M].北京：北京航空航天大学出版社，1991：10-16.

[8] 褚武杨.断裂力学基础[M].北京：科学出版社，1979：89-95.

[9] 伍颖.断裂与疲劳[M].武汉：中国地质大学出版社，2008：24-40.

[10] Paris P.C., Gomez, M.P. & Anderson, W.P. A rational analytic theory of fatigue[J]. The Trend in Engineering, 1961, 13: 9-14.

[11] Miner M. A. Cumlative damage in fatigue[J].J. Appl. Mech., 1945, 12(3): A159-164.

[12] Jaroslav Mackerle. Finite elements in the analysis of pressure vessels and piping,an Addendum:Abibliograp hy(2001-2004)[J].International Journal of Pressure Vessels and Piping., 2005, 82: 571-592.

[13] 张伟，张圣坤，等.厚壁筒内表面椭圆裂纹的应力强度因子研究[J].船舶力学，1999(4)：49-53.

Simulation Analysis of Fatigue Life of Pressure Vessel with Crack

GONG Yuli1, NIU Qingliang2
(1. CNOOC Petrochemical Engineering Co., Ltd., Jinan 250000, China; 2.Shandong Branch of Huadian Electric Power Research Institute, Jinan 250000, China)

In view of the fatigue life of the pressure vessel with cracks, the stress intensity factors of the initial cracks were calculated by using the fracture mechanics theory, the crack propagation rate was described by the Paris formula. ANSYS Workbench simulation was used to calculate the stress intensity factors and stress distribution of the pressure vessel with crack, and the fatigue life was calculated according to the calculation results. The influence of stress distribution and fatigue life were analyzed with cracks, which provided a reference for the design of pressure vessel with cracks in service.

pressure vessel; stress intensity factor; fatigue life

TQ 053.2

B

1671-9905(2017)01-0038-04

宫羽丽（1987-），硕士研究生，专业：化工过程机械，电话：18615182576

2016-11-25