具有步长调整策略的强制进化随机游走算法优化换热网络

刘璞，崔国民，肖媛，陈家星，周剑卫

（1上海理工大学新能源科学与工程研究所，上海 200093；2哈尔滨哈锅锅炉工程技术公司，黑龙江 哈尔滨 150060）

具有步长调整策略的强制进化随机游走算法优化换热网络

刘璞1，崔国民1，肖媛1，陈家星1，周剑卫2

（1上海理工大学新能源科学与工程研究所，上海 200093；2哈尔滨哈锅锅炉工程技术公司，黑龙江 哈尔滨 150060）

强制进化随机游走算法（random walking algorithm with compulsive evolution，RWCE）是一种优化换热网络的新方法，具有程序简单、算法适应性和全局搜索能力较强等优点。本文研究了最大步长对RWCE算法优化性能的影响，提出了抛物线函数的最大步长递减调整策略来平衡RWCE算法的全局搜索与局部搜索能力。将引入策略的RWCE算法与基础算法比较，发现加入最大步长递减调整策略的RWCE算法与基础RWCE算法相比，在进化后期能够跳出局部极小值，具有更强的局部搜索能力。采用10SP2、9SP和15SP换热网络实例检验加入此策略RWCE算法的有效性，其中10SP2和9SP算例的优化结果均好于文献最好结果，相比算例原始文献下降了20.98%和1.11%。对15SP算例优化找到了新的换热网络匹配结构，并好于多数无分流换热网络优化结果，且低于文献结果4.60%，证明了此方法在换热网络优化中具有较强的优化能力。

强制进化随机游走算法；换热网络优化；全局搜索能力；局部搜索能力

换热网络被广泛应用于炼油、钢铁、化工等工业生产领域，是余热回收和实现能量综合利用的关键环节，其性能的提高有利于降低产品成本，同时对于减少能源的消耗具有重要意义[1-3]。换热网络优化问题属于混合整数非线性规划问题，由不同的整型变量（物流及其匹配方式）及连续变量（换热负荷的分配）组成的系统称为一个“结构”，换热网络优化实质上是对“结构”的优化。传统的确定性方法（如牛顿法、最速下降法等），由于存在单点运算方式计算效率较低以及全局搜索能力较弱等局限，使得其运用在换热网络优化中很难取得较好的优化结果。启发式方法由于受模型非线性、非凸性和不连续影响较小被越来越多地应用于换热网络综合问题，如遗传算法[4]、模拟退火算法[5]、粒子群算法[6]、微分进化算法[7]、蚁群算法[8]等。

在运用启发式方法优化换热网络时，进化后期会受到种群多样性的限制，从而丧失全局搜索能力，学者们针对这一问题对相应的启发式方法进行了改进：文献[9]在粒子群算法的基础上结合了引力搜索算法（particle swarm optimization with gravitational search algorithm，PSO-GSA），算法将速度更新公式中加入了移动因子，通过此方法平衡算法的全局搜索能力与局部搜索能力；文献[10]采用动态更新策略改进微分进化算法提高算法的全局搜索能力，并在换热网络的运用中得到了相比基础微分进化算法更好的结果；文献[11]将基于罚因子协进化机制的微分算法应用于换热网络优化问题，同步优化罚因子与解变量，保证算法的优化精度；文献[12]设计出了一种改进的实数自适应遗传算法，提出了自适应交叉概率和变异概率来提高搜索后期效率，避免搜索后期易早熟收敛的现象；文献[13]提出了动态自适应调整信息素的蚁群算法来平衡扩大搜索空间和寻找最优解之间的关系。然而，以上的改进算法仍然很依赖种群中个体之间的信息交流，进化后期由于种群多样性缺失依旧会陷入局部极小值，很难使优化质量得到显著的提高，而难以找到全局最优解。

启发式方法进化后期易陷入局部极小值，由此产生了一种全新的强制进化随机游走算法（randon walking algorithm with compulsive evolution，RWCE），通过各换热单元热负荷的随机扩大或缩小，以及换热器数目的随机增加或消除，实现整型变量优化（换热网络结构优化）和连续变量优化（换热单元热负荷精细搜索）的同步进行；通过弱化种群中个体之间的信息交流，保持种群的多样性，从而保证算法在优化过程始终保持较强的全局搜索能力。

本文通过研究最大步长对RWCE算法全局搜索能力与局部搜索能力的影响，提出适应进化进程的步长调整策略，即抛物线函数的最大步长递减策略。通过在进化过程中调整最大步长来平衡RWCE算法在换热网络优化中的换热网络结构优化与换热单元热负荷精细搜索，提高算法的性能，最后通过换热网络优化实例验证策略的有效性。

1 换热网络优化模型

1.1 换热网络优化模型

采用换热网络无分流的分级超结构模型[14]，目标函数以年综合费用f（单位$/a）为基础，其数学描述为式(1)。

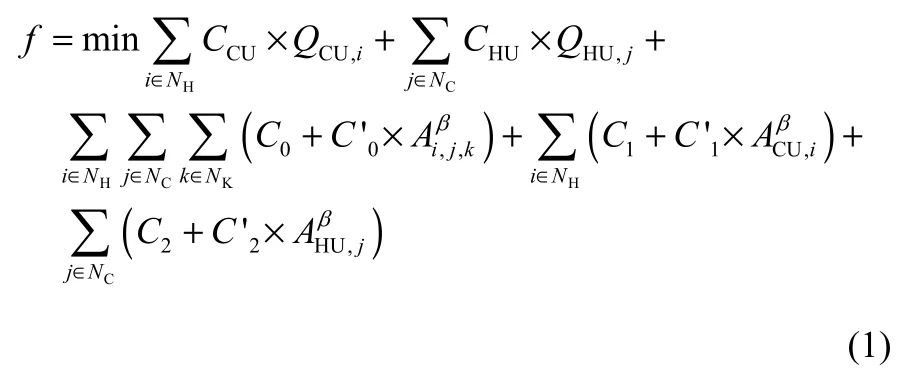
式中，i、j为热流股和冷流股编号；k为级数编号；NH、NC为热流体和冷流体的数目；NK为换热网络的级数；CCU、CHU为冷热公用工程费用系数，$/(kW·a)；QCU，i、QHU，j为冷热公用工程换热量，kW；Ai，j，k为第i股热流体与第j股冷流体在换热网络匹配第k级换热器的换热器面积，m2；ACU，i、AHU，j为冷热公用工程单元的换热面积，m2；C0、C1、C2为换热器单元和冷热公用工程单元固定投资费用，$/a；C′0、C′1、C′2分别为换热器单元和冷热公用工程单元面积费用系数；β为面积费用指数。前二项代表公用工程运行费用，后三项分别代表换热器、冷公用工程、热公用工程的面积费用。

在优化过程中，以单个换热器的热负荷为优化变量，模型中冷热流体为逆流布置，则对于每个换热器，有如式(2)、式(3)热平衡关系式。

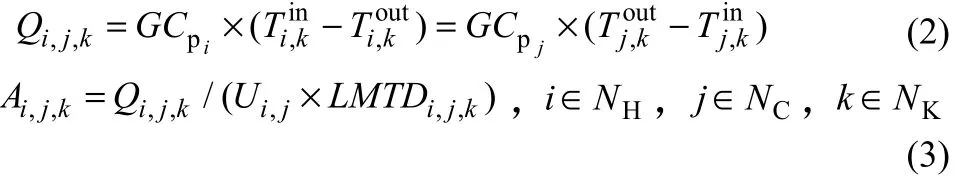
式中，Qi，j，k表示第i股热流体与第j股冷流体在换热网络匹配第k级换热器的热负荷，kW；分别为第i股热流体与第j股冷流体的热容流率，kW/℃；为第i股热流体在换热网络匹配第k级换热器的进出口温度，℃；为第j股冷流体在换热网络匹配第k级换热器的进出口温度，℃；Ui,j为对流传热系数，kW/(m2·℃)；LMTDi，j，k为对数平均温差计算公式如式(4)。

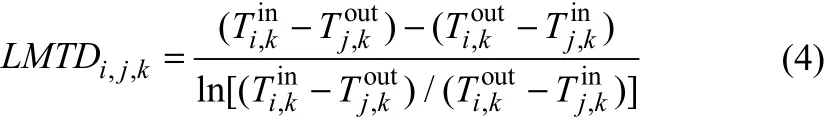
当冷热流股的热容流率相等时，即GCpi＝GCpj，采用算术平均温差代替对数平均温差，即式(5)。

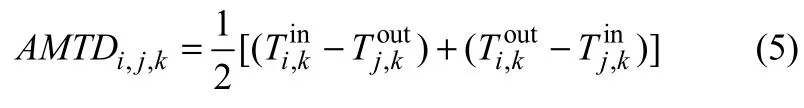
1.2 主要约束

（1）每股流体能量平衡[式(6)、式(7)]

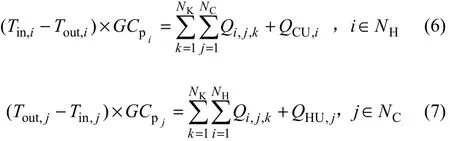
式中，Tin，i、Tout，i表示流股编号为i的热流体入口与出口温度，℃，Tin，j、Tout，j表示流股编号为j的冷流体入口与出口温度，℃。

（2）换热器进出口温度大小关系约束[式(8)、式(9)]

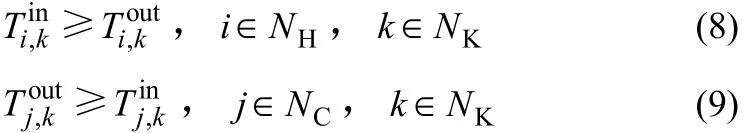
（3）出口温度约束[式(10)、式(11)]

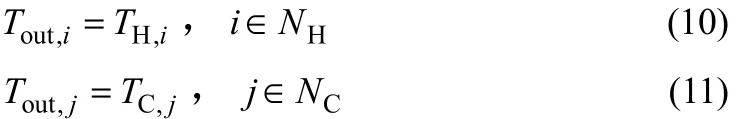
式中，TH，i、TC，i分别为冷、热流体的目标温度，℃。

（4）换热单元面积[式(12)]

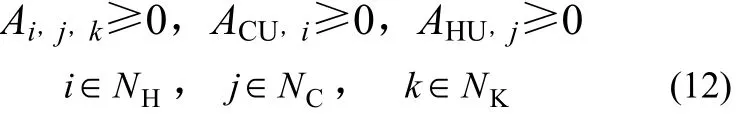
（5）换热单元的换热量[式(13)]。

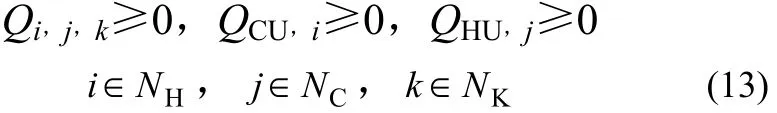
式中，Qi，j，k为换热器单元的换热量，kW。

2 强制进化随机游走算法

针对启发式方法进化后期易陷入局部极小值问题而提出的强制进化随机游走算法（RWCE），具有较强的全局搜索能力和算法适应性。RWCE算法能够同时实现整型变量和连续变量的同步优化，以年综合费用最低作为导向随机地扩大或者缩小换热器的个数进行换热网络的结构优化，弱化种群中个体间的信息交流，当优化进入局部极小值时，赋予其一定的概率去接受差解，使其能够不断跳出局部极小值而保持种群具有较高的多样性。算法流程如下所述。

（1）种群初始化

随机产生一个初始种群，其中包含N个个体，每个个体对应一个换热网络结构。随机决定每个换热器是否存在，若换热器存在，则按式(14)赋予该换热器一个随机的初始换热量。

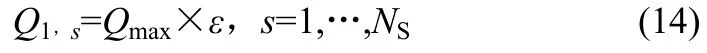
其中，Q1，s中“1”代表该种群为进化迭代前的初始种群，Qmax为求解域的大小，kW；s为个体中各换热器的编号；ε为（0，1）区间均匀分布的随机数。NS为每个换热网络结构的所有换热器均存在时换热器的个数NS=NH×NC×NK。

（2）进化阶段

更新种群每个个体的进化公式为式(15)。

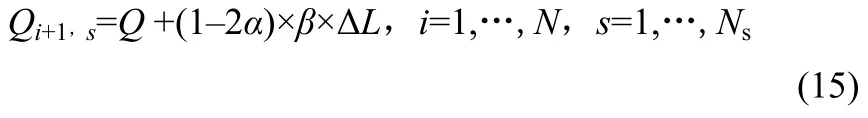
式中，α和β为（0，1）范围内均匀分布的随机数；ΔL为随机游走的最大步长，kW；i为种群中的个体编号。

当种群新个体Qi+1，s≤ΔL×η时，则令Qi+1，s＝0kW，消去该位置的换热器，其中η为可保留的最小换热量和游走最大步长ΔL的比例系数，称为保留系数。

（3）选择阶段

计算进化之后形成新个体换热网络结构的年综合费用f(Qi+1，s)，若年综合费用比原个体费用f(Qi，s)小，则用进化后新个体去代替原个体换热网络结构，并返回(2)进入下一次迭代。

（4）变异阶段

若年综合费用大于原个体费用，则赋予新个体一个“接受”差解的概率δ来接受新换热网络结构返回(2)进入下一次迭代。δ取值一般较小，一般取值不大于1%。

3 最大步长分析及递减调整策略的提出

由进化公式(9)可知，最大步长ΔL的选取直接影响到RWCE算法的搜索精度和搜索能力，同时，ΔL×η作为判断换热单元是否存在的临界尺度，一方面影响着进化过程中换热器的消去或生成，另一方面影响着进化后期种群逼近局部极小值的精密性。本文通过换热网络实例对ΔL进行深入研究，探寻ΔL影响算法全局搜索与局部搜索能力的规律，提出了ΔL随优化进程递减调整的策略来平衡RWCE算法在换热网络优化中的结构优化与精细搜索能力。

3.1 最大步长对算法的影响分析

本文以10SP2算例为例，分析RWCE算法最大步长ΔL对优化过程的影响。其中算法中种群规模N=100、求解域的大小Qmax=1000kW、保留系数η=0.9、“接受”差解的概率δ=0.01，ΔL分别取30kW、100kW和200kW，最大迭代次数ITmax为10×106，其优化过程如图1所示。

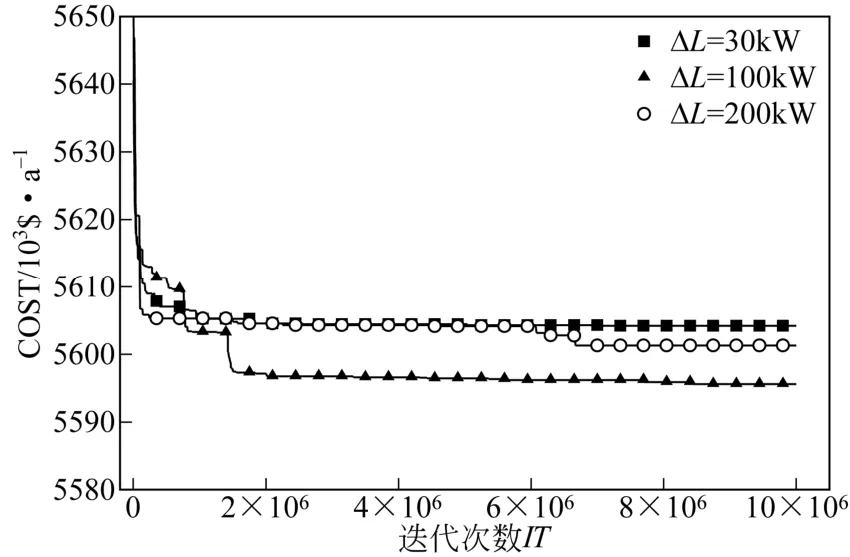
图1 不同最大步长对进化过程影响

当ΔL为30kW、100kW和200kW时，优化结果分别为5604223$/a、5595577$/a，5601285$/a，对比文献已有的优化结果，表明了基础RWCE算法具有较好的优化性能。当ΔL取30kW时，在经过约1000k次迭代之后优化费用的下降就变得极为缓慢，并且在费用下降过程中过早地趋于平缓；而当ΔL取200kW时，进化前期能够较快地降低目标费用，在进化后期也出现了费用的降低，但后期目标费用的下降大部分时间都处于“停滞”状态，缺乏不断下降的动力；相比之下ΔL取100kW时在前期能够较快地降低目标费用，但在后期仍出现费用下降缓慢的现象。当ΔL的选取偏小时（如ΔL=30kW），会极大地增加搜索到全局最优区域的时间，降低前期全局搜索效率；当ΔL的选取偏大时（如ΔL=200kW），算法的全局搜索能力增强，但容易造成局部极值左右的跳跃，从而导致算法局部搜索能力降低；即使当如ΔL的选取较合适时(如ΔL=100kW)，进化后期仍存在局部搜索能力较低的问题。这就使得基础RWCE算法的ΔL具有很大的改进潜力。

3.2 最大步长递减策略

如图2所示的二维目标函数等值线，当最大步长选取偏大（ΔL1）时，虽然进化前期搜索范围较大（如图中虚线区域所示），全局搜索能力较强，但后期搜索往往容易越过最优值区域Minimum，所以很难在后期搜索到较好的结果；当最大步长选取偏小（ΔL2）时，局部搜索能力增强，但进化前期全局搜索能力大大降低，往往每次迭代只能搜索很小范围内的区域，从而增加了搜索的时间；如果进化前期利用较大的最大步长，保证算法具有较好全局搜索能力并搜索到最优值区域Minimum附近的临近区域，进化后期利用较小最大步长在临近区域中进行精细搜索（ΔL3），从而找到Minimum，这样保证了算法同时具有较好的全局搜索能力与局部搜索能力，故而提出了最大步长ΔL随进化过程递减的策略。在算法进化过程中根据搜索时期的变化动态的更新ΔL的取值，将开口向上的抛物线函数的变化规律应用于ΔL的调整，更新公式为式(16)。

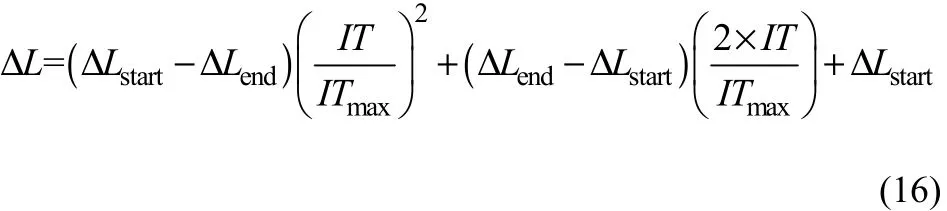
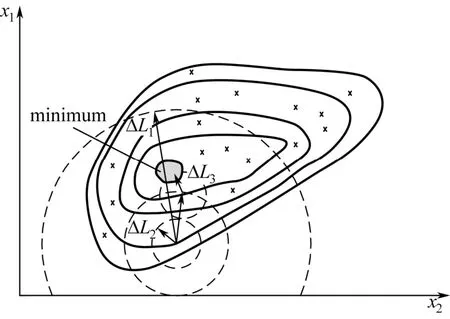
图2 二维目标函数等值线及不同LΔ情况下的优化过程

式中，ΔLstart为起始最大步长，kW；ΔLend为优化到达最大迭代次数的最大步长，kW；IT为当前迭代次数；maxIT为最大迭代次数。针对于不同的换热网络算例，可以通过调整ΔLstart和ΔLend达到各策略与不同算例的适应，其选取与求解域Qmax的大小有关，一般情况下求解域Qmax越大ΔLstart和ΔLend也相应越大。加入最大步长ΔL递减策略的RWCE算法流程图如图3所示。

3.3 最大步长递减策略的效果分析

本文采用文献[15]换热网络10SP2算例来测试所提出的策略，并将进化过程和优化结果与基础RWCE算法进行对比。10SP2算例换热器面积计算公式为60A$/a，无固定投资费用，冷公用工程费用为15$/(kW·a)，热公用工程费用为100$/(kW·a)，换热器、冷却器和加热器的传热系数均为0.025kW/(m2·℃)，其他物流参数见表1。算法中种群规模N=100、求解域的大小Qmax=1000kW、保留系数η=0.9、“接受”差解的概率δ=0.01，ΔLstart和ΔLend分别取100kW和30kW。

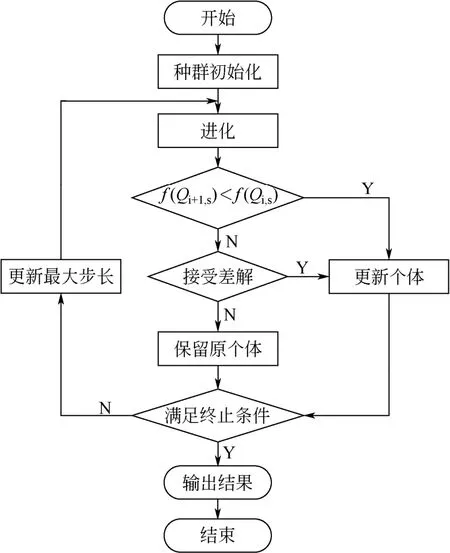
图3 加入最大步长ΔL递减策略的RWCE算法流程图

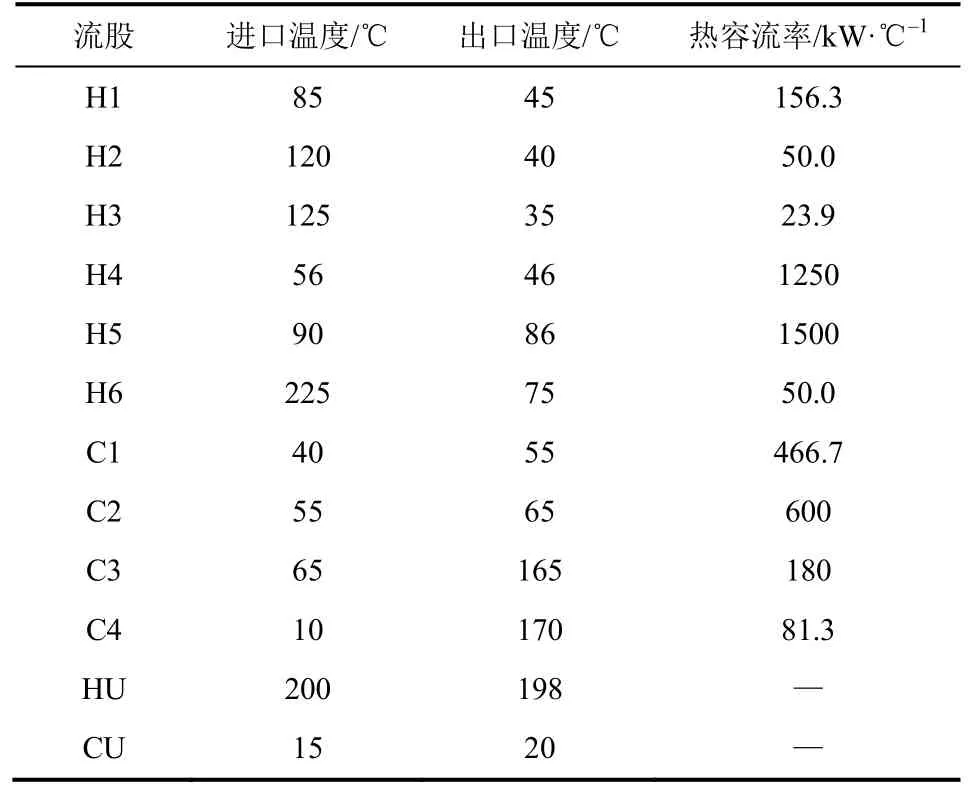
表1 10SP2流体参数表

图4绘制出了加入递减策略的RWCE算法在优化10SP2算例的过程中平均年综合费用随迭代次数的变化曲线（图中的曲线F3），并将其与ΔL=100kW，优化结果为5595557$/a的基础RWCE算法优化曲线进行比较，算法其他参数均相同，迭代次数为10×106次。

由图4可以看出，与基础RWCE算法相比，加入递减策略的RWCE算法在进化前期年平均费用下降较慢，但策略的加入有效改善了基础算法在进化后期所出现的目标费用下降趋于平缓的现象，使得算法年平均费用在进化全过程保持不断地大幅度下降，最终得到的优化费用为5589631$/a明显优于基础RWCE算法的5595557$/a。

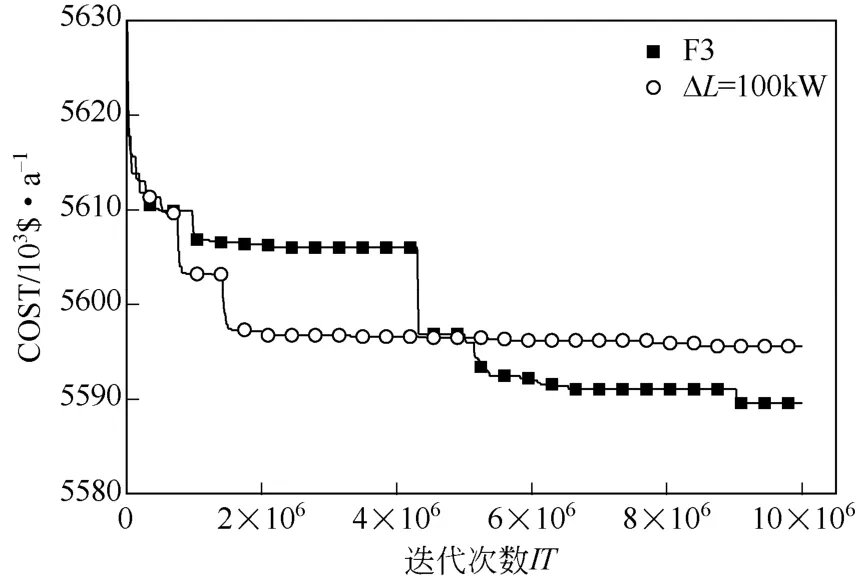
图4 加入ΔL递减策略的RWCE算法优化过程对比图

由10SP2算例测试可知，ΔL随优化进程递减更新策略的加入，使算法在进化前期具有足够强大的全局搜索能力去进行换热网络的结构优化，并找到局部极值区域临近的点；在进化后期增强了RWCE算法的局部搜索能力，使其能够更好地进行换热网络单元热负荷的精细搜索，从而提升了算法的优化性能。与此同时，策略的加入并没有改变RWCE算法种群中个体之间较弱的信息交流，从而保持了种群的多样性，保证算法在优化过程始终具有较强的全局搜索能力。

4 算例验证

算法的编程通过Fortran77软件，所有算例的优化由同一台计算机完成，计算机采用Intel(R) CUP E5-2670v3@2.30GHz（双核），内存64.0GB，64位操作系统。

4.1 算例一

算例一采用文献[15]中的10SP2算例，其物流参数与费用计算公式见文章3.3节及表1，利用加入策略的RWCE算法优化算例，得到的优化结果为5589631$/a，较算例原始文献[15]优化结果低20.98%，优化时间6676.97s，优化结构如图5所示。

由图4可知，结合递减策略的RWCE算法在进化迭代1000k次的时候就已经达到了5607281$/a，已经低于大部分的文献[15-19]，随着迭代的不断进行，ΔL随抛物线函数递减，算法的局部搜索能力逐渐增强，极大地减小了优化费用在局部极值左右跳跃的可能性，从而使算法在后期能够更好地实现换热单元热负荷的精细搜索。最终得到的结果较文献[18]低30496$/a，较文献[19]低6448$/a，与其他文献的优化费用对比如表2所示。

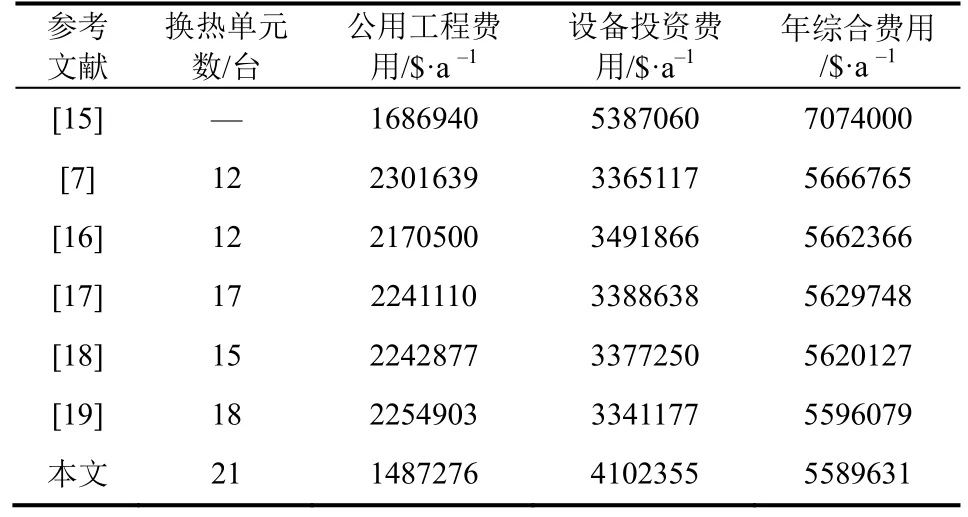
表2 算例一的优化费用对比

4.2 算例二

算例二采用文献[20]中的9SP算例，由4股热流体和5股冷流体组成。换热器面积计算公式为2000+70A$/a，热公用工程费用为60$/(kW·a)，冷公用工程费用为6$/(kW·a)，算例参数如表3所示。算法种群规模N=100、求解域的大小Qmax=1000kW、保留系数η=0.9、“接受”差解的概率δ=0.01，ΔLstart和ΔLend分别取100kW和30kW。

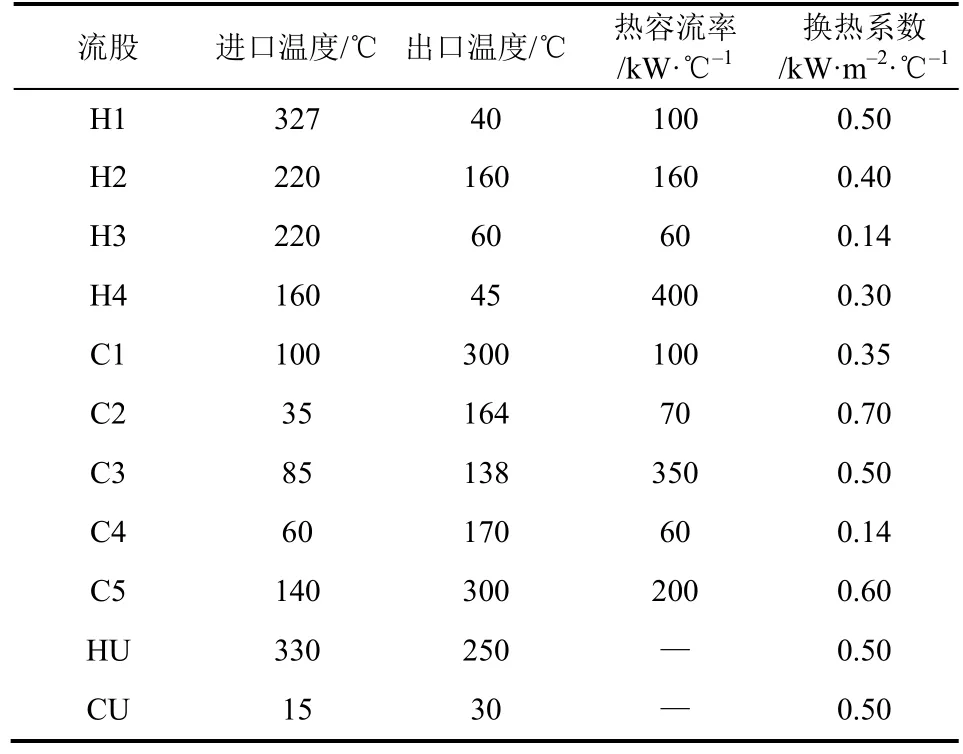
表3 算例二流体参数表

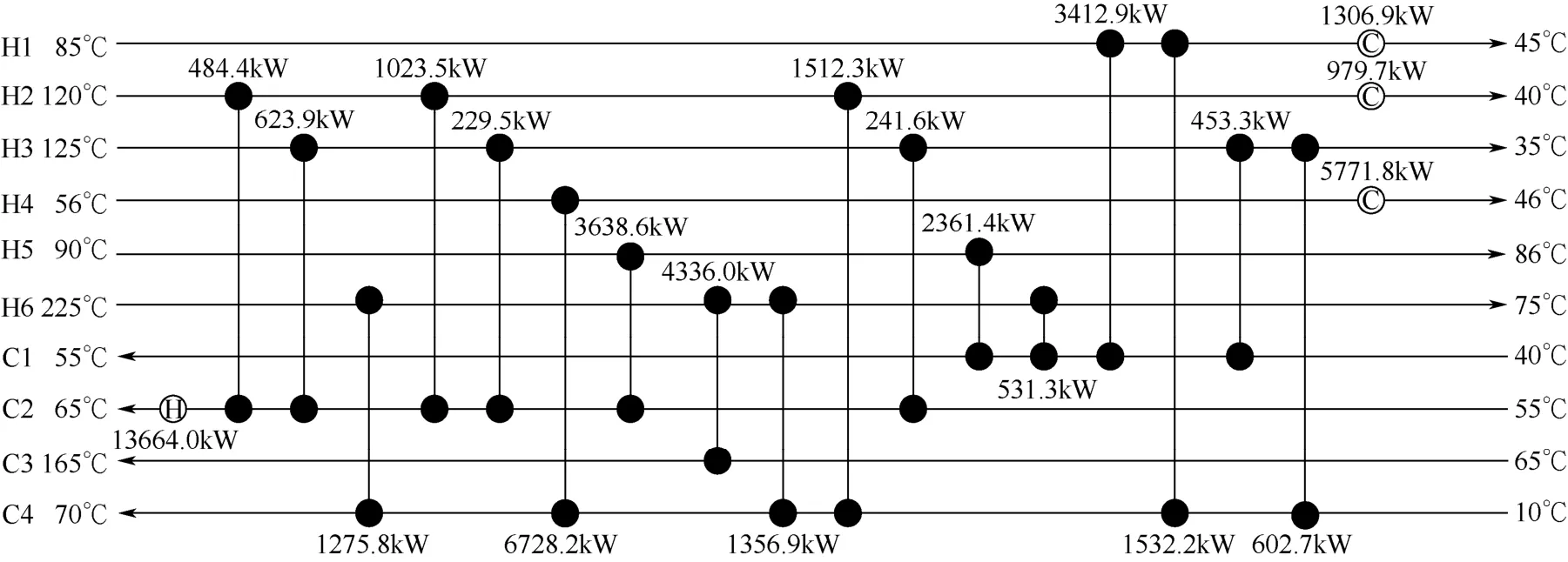
图5 算例一换热网络结构图

采用结合递减策略的RWCE算法，得到的最终优化结果为2927081$/a，较算例原始文献[20]结果低1.11%，优化时间11012.11s，相比文献[18]采用微分进化算法优化该算例的结果低17621$/a，微分进化算法受种群多样性限制，最终会陷入局部极值点，文献[10]采用动态更新策略改进微分进化算法试图解决该问题，得到较好的优化结果2931042$/a，但是其种群中个体之间仍然存在信息交流，进化后期依旧会由于种群多样性的缺失而陷入局部极值，使得采用递减策略的RWCE算法优化算例结果比文献[10]低3961$/a，优化结构如图6所示。

4.3 算例三

算例三取自文献[22]的15SP算例，过程流体由8股热流体和7股冷流体组成，换热器面积计算公式为8000+500A0.75$/a，热公用工程费用为80$/(kW·a)，冷公用工程费用为10$/(kW·a)，算例的其他参数如表5所示。

用加入递减策略的RWCE算法进行优化，其中种群规模N=100、求解域的大小Qmax=1500kW、保留系数η=0.9、“接受”差解的概率δ=0.01，由于算法求解域较大，ΔLstart和ΔLend分别取130kW和40kW。找到了新的换热网络结构，得到最终优化结果为1525561$/a，较文献[22]优化结果低4.60%，优化时间48791.81s，优化结构如图7所示。优化结构中换热器的个数介于文献[23-25]优化结果之间，并无明显增加；优化费用均好于文献[22-25]无分流换热网络优化结果，且较文献[25]低34170$/a；优化结果相比文献[26]的优化结果高14670$/a，而文献[26]采用了有分流的换热网络模型，与本文数学模型不同。与其他文献的优化费用及换热器个数对比如表6所示。

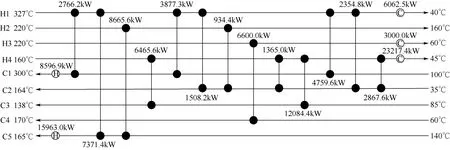
图6 算例二换热网络结构图

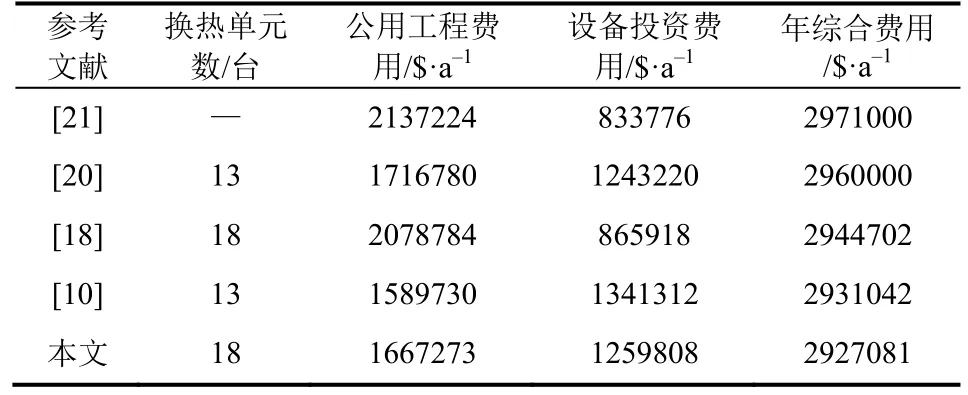
表4 算例二的优化费用对比

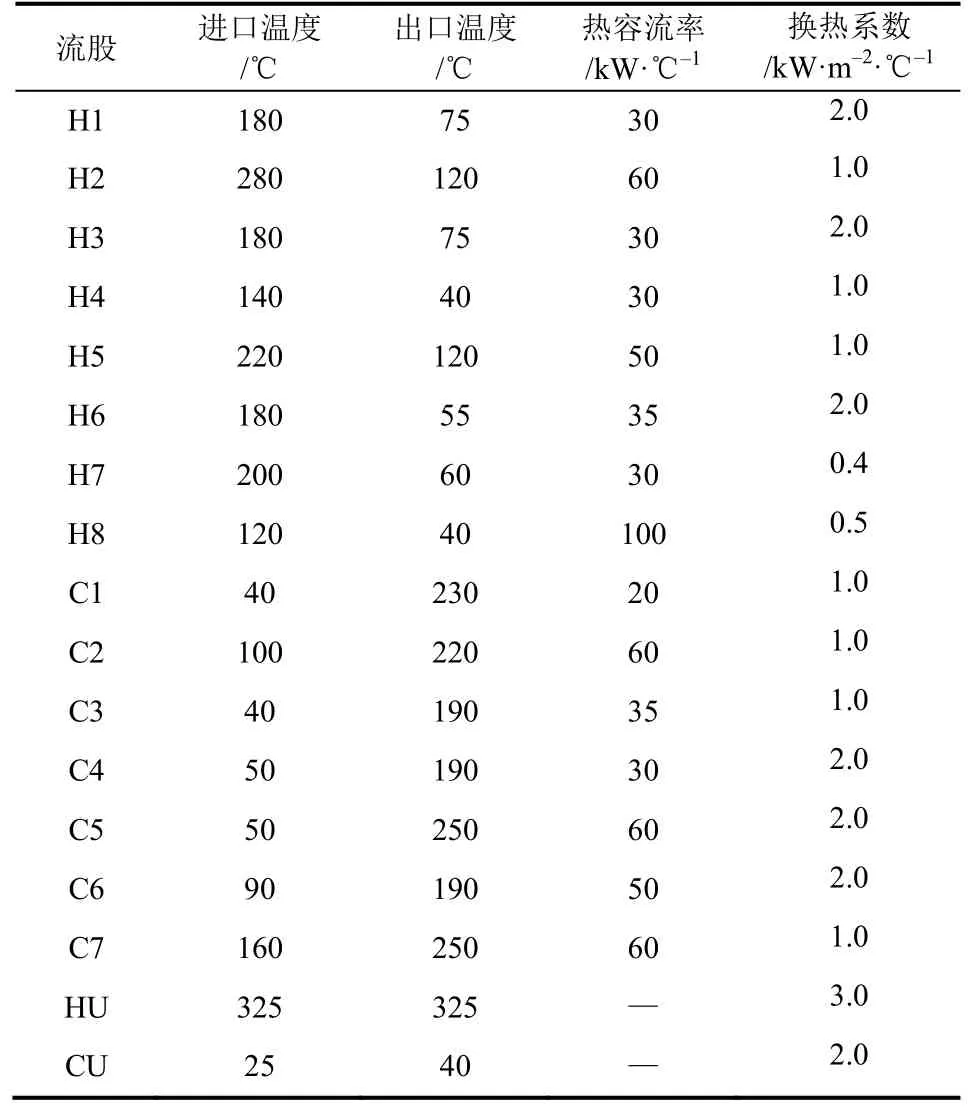
表5 算例三流体参数表

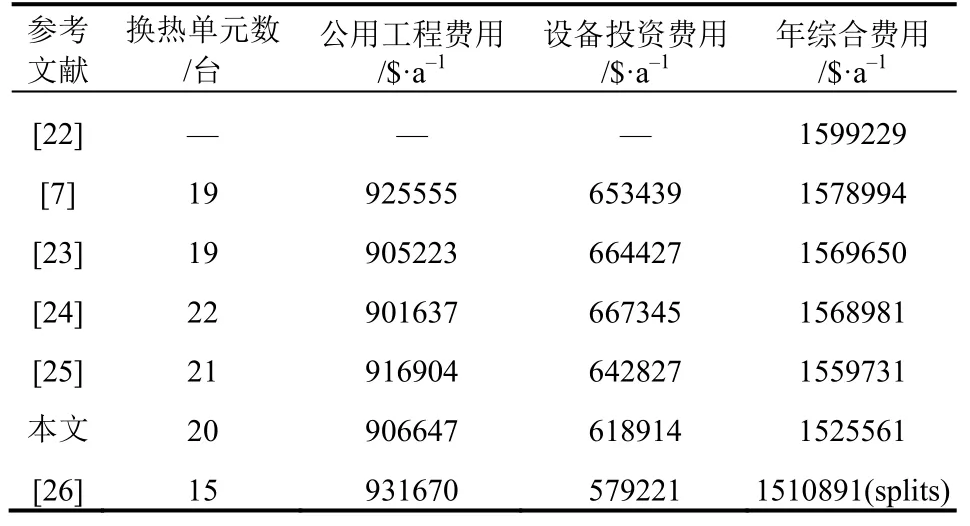
表6 算例三的优化费用对比

5 结论

（1）强制进化随机游走算法（RWCE）中的最大步长ΔL直接影响到算法的全局搜索与局部搜索能力，且当ΔL过小时会极大地增加搜索的时间，降低搜索效率；当ΔL过大时后期搜索容易造成局部极值左右的跳跃，很难找到很好的解。因此，RWCE算法中ΔL具有很大的改进潜力。

（2）提出了对ΔL的改进策略，将原本在优化全程固定不变的ΔL，改进为ΔL在进化进程中随抛物线函数递减，并通过10SP2算例对策略进行测试分析。

（3）经过10SP2算例测试分析，发现抛物线递减策略结合RWCE算法在保证原算法优化前期具有足够强大全局搜索能力的基础上，增强了算法在后期的局部搜索能力，提升了算法的优化性能。同时，策略的加入并未改变算法原本种群中个体之间较弱的信息交流，因此算法在后期依旧具有较好的多样性，能不断跳出局部最优解。

（4）采用递减策略的RWCE算法优化10SP2算例得到的优化结果为5589631$/a，好于目前已知的绝大部分文献。本文还通过其他两个算例验证了策略有效性，均得到较不错的优化结果，其中优化算例三得到的年综合费用为1525561$/a，均低于目前文献中的优化费用；优化算例二得所到的年综合费用2927081$/a也低于目前绝大部分文献使用其他优化方法得到的费用。

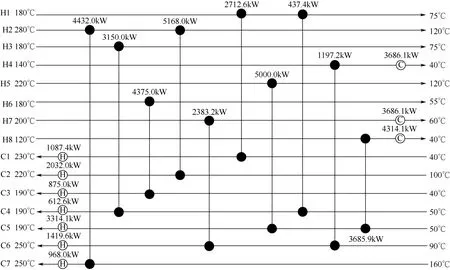
图7 算例三换热网络结构图

[1] NAKAIWA M，HUANG K，ENDO A，et al. Internally heat-integrated distillation columns：a review[J]. Chemical Engineering Research & Design，2003，81（1）：162-177.

[2] LINNHOFF B，DUNFORD H，SMITH R. Heat integration of distillation columns into overall processes[J]. Chemical Engineering Science，1983，38（8）：1175-1188.

[3] PREMKUMAR R，RANGAIAH G P. Retrofitting conventional column systems to dividing-wall columns[J]. Chemical Engineering Research & Design，2009，87（1）：47-60.

[4] RAVAGNANI M A S S，SILVA A P，ARROYO P A，et al. Heat exchanger network synthesis and optimisation using genetic algorithm[J]. Applied Thermal Engineering，2005，25（7）：1003-1017.

[5] ATHIER G，FLOQUET P，PIBOULEAU L，et al. Optimization of heat exchanger networks by coupled simulated annealing and NLP procedures[J]. Computers & Chemical Engineering，1996，20（12）：S13–S18.

[6] SILVA A P，RAVAGNANI M A S S，BISCAIA E C，et al. Optimal heat exchanger network synthesis using particle swarm optimization[J]. Optimization & Engineering，2008，11（3）：459-470.

[7] YERRAMSETTY K M，MURTY C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering，2008，32（8）：1861-1876.

[8] 万义群，崔国民. 蚁群算法在换热网络优化中的应用[J]. 能源研究与信息，2013，29（4)：234-238. WAN Y Q，CUI G M. Application of ant colony algorithm in optimization of heat exchanger networks[J]. Energy Research and Information，2013，29（4）：234-238

[9] SUN S，PENG Q. A hybrid PSO-GSA strategy for high-dimensional optimization and microarray data clustering[C]// IEEE International Conference on Information and Automation，2014.

[10] 陈上，崔国民，彭富裕，等. 采用动态更新策略的微分进化算法优化换热网络[J]. 热能动力工程，2015，30（4）：509-514. CHEN S，CUI G M，PENG F Y，et al. Optimization of the heat exchanger network by differential evolution algorithm based on dynamic update strategy[J]. Journal of Engineering for Thermal Energy & Power，2015，30（4）：509-514.

[11] 方大俊，崔国民，许海珠，等. 基于罚因子协进化微分算法优化换热网络[J]. 高校化学工程学报，2015，29（2）：407-412. FANG D J，CUI G M，XU H Z，et al. Optimization of heat exchanger networks with cooperation differential evolution algorithm based on penalty factors[J]. Journal of Chemical Engineering of Chinese Universities，2015，29（2）：407-412.

[12] 潘伟，刁华宗，井元伟. 一种改进的实数自适应遗传算法[J]. 控制与决策，2006，21（7）：792-795. PAN W，DIAO Z H，JING Y W. An improved real-value adaptivegenetic algorithm[J]. Control & Decision，2006，21（7）：792-795.

[13] 覃刚力，杨家本. 自适应调整信息素的蚁群算法[J]. 信息与控制，2002，31（3）：198-201. QIN G L，YANG J B. An improved ant colony algorithm based on adaptively adjusting pheromone[J]. Information & Control，2002，31（3）：198-201.

[14] YEE T F，GROSSMANN I E，Kravanja Z. Simultaneous optimization models for heat integration—Ⅰ. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & Chemical Engineering，1990，14（10）：1165-1184.

[15] AHMAD S. Heat exchanger networks：cost tradeoffs in energy and capital[D]. Manchester：University of Manchester Institute of Science and Technology（UMIST），1985.

[16] KHORASANY R M，FESANGHARY M. A novel approach for synthesis of cost-optimal heat exchanger networks[J]. Computers & Chemical Engineering，2009，33（8）：1363-1370.

[17] 肖媛，崔国民，彭富裕，等. 粒子群算法在非线性系统应用中的早熟现象及其改进[J]. 计算物理，2015，32（6）：693-700. YUAN X，CUI G M，PENG F Y，et al. An improved particle swarm optimization for precocious phenomenon in nonlinear system engineering[J]. Chinese Journal of Computational Physics，2015，32（6）：693-700..

[18] 方大俊，崔国民. 微分进化算法应用于换热网络全局最优化[J]. 化工学报，2013，64（9）：3285-3290. FANG D J，CUI G M. Global optimization of heat exchanger networks using differential evolution algorithm[J]. CIESC Journal，2013，64（9）：3285-3290.

[19] PENG F，CUI G. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm[J]. Applied Thermal Engineering，2015，78：136-149.

[20] LINNHOFF B，AHMAD S. Cost optimum heat exchanger networks—Ⅰ. Minimum energy and capital using simple models for capital cost[J]. Computers & Chemical Engineering，1990，14（7）：729-750.

[21] BRIONES V，KOKOSSIS A C. Hypertargets：a conceptual programming approach for the optimisation of industrial heat exchanger networks-Ⅰ. Grassroots design and network complexity[J]. Chemical Engineering Science，1999，54（5）：685–706.

[22] BJÖRK K M，NORDMAN R. Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J]. Chemical Engineering & Processing，2005，44（8）：869-876.

[23] LEWIN D R. A generalized method for HEN synthesis using stochastic optimization —Ⅱ. The synthesis of cost-optimal networks[J]. Computers & Chemical Engineering，1998，22（10）：1387-1405.

[24] 胡向柏，崔国民，许海珠，等. 换热器优化顺序对换热网络全局优化的影响[J]. 化工进展，2012，31（5）：987-991. HU X B，CUI G M，XU H Z，et al. Influent of optimization order of heat exchanger on the global optimization result of heat exchanger networks[J]. Chemical Industry & Engineering Progress，2012，31（5）：987-991.

[25] 方大俊，崔国民，许海珠，等. 基于蒙特卡罗微分算法优化大规模换热网络[J]. 化学工程，2014，42（5）：66-71. FANG D J，CUI G M，XU H Z，et al. Optimization of heat exchanger networks based on mixed strategy of Monte Carlo and differential evolution algorithm[J]. Chemical Engineering，2014，42（5）：66-71.

[26] FIEG G，LUO X，JEŻOWSKI J. A monogenetic algorithm for optimal design of large-scale heat exchanger networks[J]. Chemical Engineering & Processing Process Intensification，2009，48（s11/s12）：1506-1516.

Optimizing heat exchanger network by random walking algorithm with compulsive evolution combined with step length adjustment strategy

LIU Pu1，CUI Guomin1，XIAO Yuan1，CHEN Jiaxing1，ZHOU Jianwei2
（1Research Institute of New Energy Science and Technology，University of Shanghai for Science and Technology，Shanghai 200093，China；2Harbin Boiler Engineering Technology Company，Harbin 150060，Heilongjiang，China）

Random walking algorithm with compulsive evolution（RWCE） is a novel heuristic method to optimize heat exchanger networks，which has a powerful global optimizing ability in the process of evolution. In this paper，the effect of maximal step length on the performance of RWCE algorithm was studied. To efficiently control the global and local search ability of the algorithm，a decreasing maximal step length adjustment strategy based on a parabola opening downwards curve was proposed. Compared with the basic algorithm，the strategy is capable of jumping out of local optima in the late evolution stage and strengthening the local search ability. The optimal results of three HEN cases（10SP2，9SP and 15SP） from literatures were used to test the effectiveness of the RWCE algorithm cooperated with proposed strategy. The results of former two（10SP2 and 9SP ）are better than the best results published，which is 20.98% and 1.11% lower than the original literature results. A new heat exchanger networks structure was found in case 3（15SP），which is better than the majority of optimal results of no stream splits and 4.6% lower than the literature results. The results of these three cases demonstrate that the method enjoys a better optimization capability in the global optimization of heatexchanger network.

random walking algorithm with compulsive evolution（RWCE）；heat exchanger network synthesis（HENS）；global searching ability；local search capability

TK124

：A

：1000–6613（2017）02–442–09

10.16085/j.issn.1000-6613.2017.02.006

2016-06-17；修改稿日期：2016-09-17。

上海市科委部分地方院校能力建设计划（16060502600）、国家自然科学基金（51176125）及沪江基金研究基地专项（D14001）项目。

刘璞（1993—），男，硕士研究生，主要从事强化传热及过程系统优化研究。联系人：崔国民，教授，博士生导师，主要从事强化传热及高效换热器研究。E-mail：cgm1226@163.com。