多粒径颗粒在圆形偏心滚筒内的运动混合
张立栋,李连好,秦宏,王擎
(东北电力大学油页岩综合利用教育部工程研究中心,吉林 吉林 132012)
多粒径颗粒在圆形偏心滚筒内的运动混合
张立栋,李连好,秦宏,王擎
(东北电力大学油页岩综合利用教育部工程研究中心,吉林 吉林 132012)
采用离散单元法(DEM),对5种粒径颗粒在滚筒内的运动混合进行数值模拟,研究了偏心距对滚筒内颗粒体系分区及区域变化、大颗粒速度变化和多粒径颗粒混合程度的影响。结果表明;非偏心滚筒内处于滚落运动模式的颗粒体系分为3个区域:平流层、活动层和涡心;偏心滚筒内不存在实际的涡心,随着滚筒转动,“移动涡心”的形状大小和位置都在周期性变化。在不同颗粒运动周期中,非偏心滚筒内的大颗粒在平流层中的匀速度基本相等;而在偏心滚筒内,大颗粒在相邻两次平流层中的两次匀速度基本都不相等,且偏心距越大的滚筒内,颗粒匀速度的变化越明显。偏心距基本不影响滚筒内多粒径颗粒的接触效果,多粒径颗粒在滚筒内的混合过程中,接触数的变化类似阻尼振动曲线变化。
离散单元法;偏心滚筒;多粒径颗粒;移动涡心
颗粒是物质存在的普遍形态,也是工业生产中必不可少的物料,利用滚筒将不同物性颗粒进行混合是药品制造、建材加工、金属冶炼和化肥生产等行业进行工艺处理的重要操作单元[1-2],因此,研究颗粒在滚筒内的运动混合特性对于生产指导和工程应用具有重要意义。
正是由于颗粒在滚筒内运动混合的工业广泛性和技术实用性,国内外研究者对其做了大量研究工作[3-5]。其中,陈辉等[6]通过离散单元法模拟了滚筒内二元颗粒在滚落运动模式下的混合过程,分析了颗粒尺寸和密度等颗粒自身物性因素对混合过程的影响,发现增大体积比和密度比会使混合过程中的二元颗粒产生分离。欧阳鸿武等[7]实验研究了不同尺寸、不同形状的颗粒在低速转鼓内的运动变化情况,发现流动层厚度随剪切率增大而减小,随转速增大而增大。另外,JIANG等[8]和张立栋等[9-10]分别在滚筒中心或者内壁设置不同形状挡板,研究了滚筒的结构形状因素对筒内二元颗粒混合效果的影响,结果表明,挡板能够有效地增强颗粒之间混合。李少华等[11]和闫明等[12]又对比分析了圆形、椭圆形和方形混合器内二元颗粒分离与混合的复杂过程,发现混合器形状的差异对二元颗粒混合的稳定性有很大影响。
除了颗粒自身物性、滚筒结构形状外,操作参数也是影响滚筒内颗粒运动混合的重要因素。AMARA等[13]和CHOU等[14]分别研究了颗粒动态安息角和活动层厚度在不同填充率和不同转速影响下的变化规律。赵永志等[15]采用离散单元法对滚筒内二元颗粒的流动过程进行了数值模拟,分析了滚筒填充率、转速等操作参数对二元颗粒形成花瓣模式的影响,发现在滚筒转动过程中,混合均匀的二元颗粒逐渐分离,出现大颗粒在滚筒外围、小颗粒在内核的现象。
尽管国内外研究者从多方面对滚筒内的颗粒混合进行了大量实验和模拟计算,但是他们并未改变过滚筒的运动形式,滚筒一直绕中心转轴自转,而且所研究的大多都是一元或二元颗粒,并没有涉及多粒径颗粒,而在现实生产生活中,所处理的几乎都是大小不一的多粒径颗粒。又由于通过实验很难获得滚筒内颗粒的参数信息,因此,本文采用离散单元法(DEM)对多粒径颗粒在偏心滚筒(公转运动的滚筒)内的运动混合过程进行数值研究,初步探究多粒径颗粒在偏心滚筒内的运动机理和混合规律,丰富颗粒运动混合的理论知识。
1 模拟方法
1.1 DEM模拟条件
本文以油页岩固体热载体干馏为应用背景,固体热载体干馏过程中固体热载体为1mm左右,干馏的油页岩颗粒粒径分布在2~5mm内,4种粒径颗粒筛分出的质量比约为1∶1∶1∶1。热载体与油页岩的混合比例是1∶1,热载体与油页岩密度相近,因此,物料采用与油页岩颗粒密度相同的球形颗粒,模拟中所设置的计算参数均来自实验测量或经验取值,如表1所示。模拟中滚筒的密度为7800kg/m3,弹性模量是1.82×109N/m2,泊松比为0.3。

表1 颗粒的物理参数及力学性质
1.2 几何模型
滚筒内径为84mm,厚度为20mm,本文采用离散单元法对滚筒内5种粒径颗粒的运动混合过程进行数值模拟,研究滚筒几何中心偏离滚筒旋转中心的距离P(以下简称偏心距)对多粒径颗粒运动混合的影响。3个模拟工况的偏心距分别为P0=0,P1=10mm,P2=20mm,5种不同颗粒按质量比4∶1∶1∶1∶1(粒径从小到大)且小粒径颗粒在下大粒径颗粒在上的原则向滚筒内填充,填充率为30%,滚筒以15r/min进行定速转动,转动前,转轴在颗粒体系的垂直正上方,如图1所示,黑点代表滚筒转轴在径向切面的位置。
2 混合程度评价指标
为了对比分析偏心滚筒内2mm、3mm、4mm、5mm颗粒(统称为大颗粒)与1mm颗粒之间的混合程度,需要选择一个定量指标来评价混合质量,DEM时刻记录颗粒参数的变化情况,因此,可以依据颗粒之间的接触状态以接触数作为判断混合程度的评价指标。接触数q的表达式如式(1)。
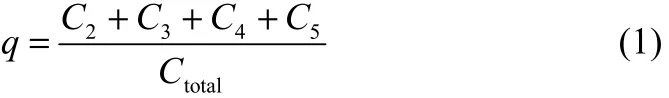
式中,C2、C3、C4和C5分别表示2mm、3mm、4mm和5mm颗粒与1mm颗粒之间的接触数;Ctotal表示总的接触数,即5种粒径颗粒之间两两相互接触的接触数总和。
由式(1)可知,q值越大,颗粒混合越均匀,q值越小,颗粒混合越差,而1mm颗粒相对较多,同粒径间接触数较大,导致q值偏小。因此,AKASH GUPTA等[16]对接触数做了研究,指出q值在0.2~0.5时,颗粒的混合效果已经较佳。
3 模拟结果分析
3.1 颗粒体系的分区
颗粒在滚筒中的运动大致分为6种模式[17]:滑移(slipping)、阶梯(slumping)、滚落(rolling)、泄落(cascading)、抛落(cataracting)和离心(centrifuging)。在工程实际中,滚落模式是最常见的颗粒运动形态,也被认为是混合效率最高的运动模式[13],文中3个模拟工况中的颗粒体系均为滚落运动模式,因此,本文将主要针对颗粒处于这种运动形态下的运动混合进行深入分析。
随着滚筒的不断转动,在P0=0,即非偏心滚筒内的5种粒径颗粒逐渐混合,同时,各个颗粒开始获得不同速度,根据颗粒的速度差异将滚筒内的颗粒体系分为3个区域:平流层、活动层和涡心,如图2所示。平流层的颗粒在滚筒内壁剪切作用下随滚筒一起绕轴线运动,颗粒速度比较均匀,为0.061m/s左右,颗粒间相对静止;活动层的颗粒由于重力作用在自由表面快速向下崩落,速度矢量比较紊乱,速度值基本大于0.090m/s,并形成稳定的动态休止角;涡心中的颗粒被平流层和活动层包裹,颗粒基本不发生位移,速度接近于0。此外,将除涡心以外的颗粒,经历一次平流层的匀速运动和一次相邻活动层的快速崩落运动的过程,定义为一个颗粒运动周期。
3.2 偏心滚筒内“移动涡心”变化
滚筒内的颗粒混合是通过平流层与活动层中不同粒径颗粒之间的不断交换来实现,尽管颗粒的相互作用基本发生在活动层和平流层,两者是颗粒混合的重要区域,而涡心是抑制颗粒混合的区域,又被称为混合死区,但是涡心区域的变化会直接影响平流层或活动层的变化,从而可能对颗粒的运动混合产生影响。因此,为深入分析颗粒在偏心滚筒中的运动混合过程,有必要先对偏心滚筒内颗粒的涡心变化进行研究。
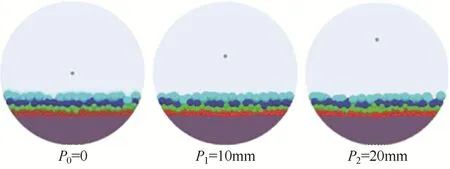
图1 滚筒内颗粒初始填充示意图
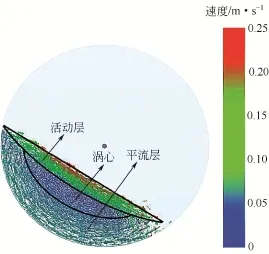
图2 滚落运动模式下颗粒分区图
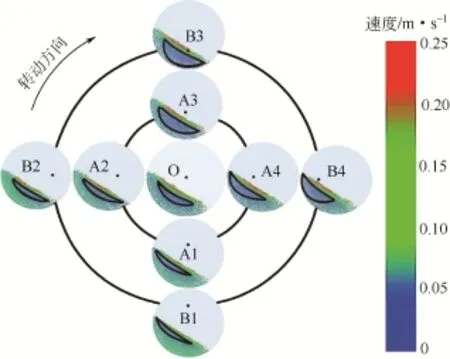
图3 3个工况中的涡心变化对比图
图3为颗粒在滚筒内达到稳定混合状态下的速度矢量图,图中O表示P0=0,A表示P1=10mm,B表示P2=20mm,1、2、3、4表示滚筒在一个运动周期内的4个不同位置。在P0=0滚筒内,黑色框选区为涡心区域,随滚筒转动,颗粒的涡心位置和大小基本不发生改变;而偏心滚筒内的黑色框选区随着滚筒地匀速转动,其位置和大小都在不断变化,如图A1-A2-A3-A4-A1的变化过程。因此,偏心滚筒内颗粒的这部分区域并非实际的涡心,虽然颗粒速度在某一时刻很小,但是区域位置却在一直改变,所以,可将偏心滚筒内的黑色框选区称为“移动涡心”。对比两种偏心距下滚筒内颗粒的速度矢量图发现:偏心滚筒内颗粒的“移动涡心”随滚筒转动发生周期性变化,“移动涡心”区域总是由小变大再逐渐变小的循环往复,这与偏心滚筒实验[18]所得结论一致。“移动涡心”的这种规律性变化与滚筒的公转运动有直接关系,滚筒在周期性转动过程中,颗粒体系相对滚筒转轴的位置也在周期性变化,因为偏心滚筒内平流层颗粒在重力和接触力的作用下作圆周运动,当颗粒体系距离转轴越来越近时,颗粒的离心运动半径越来越小,相同角速度下的线速度减小,平流层内颗粒开始减少,“移动涡心”相应增大,如图中B1-B2-B3过程;相反,当颗粒体系运动越来越远离转轴时,平流层内部分颗粒线速度不断增大导致平流层内颗粒比例增加,“移动涡心”相应减小,如图中B3-B4-B1过程,而且,偏心距越大的滚筒,“移动涡心”区域大小的变化就越显著,如图中B1比A1的移动涡心小,而B3对比A3的却更大。在偏心滚筒内,平流层与“移动涡心”没有固定界线,“移动涡心”时刻变化,颗粒在其内停留时间很短暂,因此,“移动涡心”又可看成平流层内部分区域在某一时刻的特殊状态。另外,通过观察“移动涡心”的位置变化,发现“移动涡心”总是向着靠近滚筒转轴的位置移动。
3.3 偏心滚筒内大颗粒速度变化分析
通过观察,滚筒转动一周的过程中,除了P0=0的非偏心滚筒涡心内的静止颗粒外,其他颗粒都经历两个运动周期,如图4(a)所示,针对单个颗粒而言,颗粒在平流层内基本保持匀速运动,而在活动层内先加速后减速运动,如图4(b)所示。本文主要分析大颗粒与1mm颗粒之间的运动混合情况,因此,探究大颗粒在滚筒内速度参数的变化是必要的,图4(d)为不同偏心距的滚筒内随机选取的单个5mm颗粒速度变化对比图,从图中可以看出,在P0=0的非偏心滚筒内,大颗粒处于平流层运动时的匀速度在不同颗粒运动周期中的变化很小,保持在0.061m/s左右,基本相等;而在偏心滚筒内,大颗粒经历相邻两个颗粒运动周期的两次匀速度几乎都不相等,且偏心距越大,这两次匀速度的波动越明显。这是因为,随着滚筒转动,颗粒在相邻两次平流层运动过程中,颗粒体系整体位置与转轴距离不同,相应的线速度差异较大。
由于颗粒完成两次运动周期的总时间不固定(约3.8s),而滚筒转动一周的固定时间是4s,两者相近但又有短暂延迟,如图4(a)所示,颗粒每次在匀速度较高的平流层运动时,颗粒体系的整体位置与转轴的距离在不断地增大,随着滚筒转动,距离增大到一定程度后又开始逐渐缩短,因此,较高的匀速度随时间变化先逐渐增大到0.090m/s,然后不断减小至0.071m/s,如图4(d)P2=20mm中的a-b-d过程;相反,颗粒每次在匀速度较低的平流层运动时,颗粒体系整体位置距离转轴先是越来越近,然后越来越远,较低匀速度也相应的先减小到0.027m/s后再增大至0.066m/s,如图4(d)P2=20mm中的a-c-d过程。当两者的时间延迟随滚筒转动积攒到一个颗粒运动周期的时间(约1.9s)时,最终出现图4(c)所示情况:相邻的3次匀速度大小相近。结束这种情况之后,较高匀速度与较低匀速度继续上述的规律性变化,但是每次完成这种变化的时间随颗粒运动周期所用时间的随机性而变化。
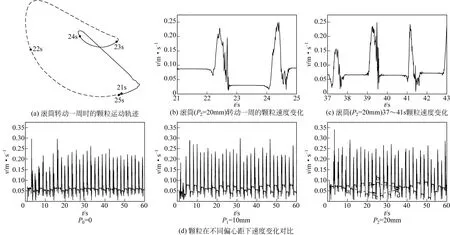
图4 单个5mm颗粒运动变化过程
3.4 颗粒混合机理及混合程度对比分析
不同粒径颗粒在滚筒内的混合程度是由混合与偏析的关系所决定,混合又是通过对流、剪切和扩散3种机制共同作用完成。如图5所示,最初填充颗粒时,不同粒径颗粒几乎完全分离(t=0s);随着滚筒转动,颗粒在内壁提升力作用下开始运动,自由表面中大颗粒向下快速崩落,产生堆积现象(t=2s),宏观运动引起不同粒径颗粒之间的位置发生较大改变,形成对流混合;滚筒继续转动,颗粒在滚筒内的随机运动,使堆积的大颗粒逐渐分散,不同粒径颗粒由于重力不同,在自由表面相互碰撞传递动量,产生速度差异,导致局部的颗粒剪切作用,同时,单个大颗粒通过渗透、分散出现在小颗粒区域,体现了局部的扩散混合(t=3s),且粒径越小的大颗粒越容易在小颗粒中扩散。颗粒的混合并不是某种单一机制的作用结果,在整个混合过程中,3种混合机制一直同时存在。然而,由于颗粒粒径的不同,在偏析作用下,滚筒内混合的颗粒体系,形成了大颗粒在外围,且平流层中粒径越大的颗粒越靠近筒壁位置分布,小颗粒聚集在中心区域的分层现象(t=7s,t=40s)。混合与偏析的共存、制约,使混合程度稳定的颗粒体系并没有达到均匀混合状态,而是保持混合与偏析动态平衡的相对稳定混合(t=60s)。
图6为3个滚筒在运动过程中筒内颗粒接触数的曲线变化对比图,从图中可以看出,3条曲线的变化趋势基本一致,接触数随时间变化由于对流混合先急剧增大,然后围绕在0.185上下大幅度波动,在滚筒不断转动过程中,颗粒接触数的波动幅度越来越小,类似阻尼振动过程中的曲线变化,直到滚筒转动至7圈或8圈后,波动幅度减小至相对稳定状态,接触数稳定在0.185左右微弱波动。另外,3条曲线的良好吻合性说明偏心距对滚筒内多粒径颗粒的接触影响较弱,因此,单一地改变偏心距一种变量虽不能改善以接触数为评价指标的混合效果,但颗粒在偏心滚筒内的运动混合等规律性变化属机理性初探,其相关的实际应用价值还有待进一步的深入探讨和研究。
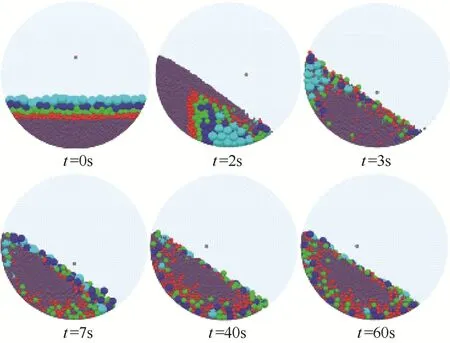
图5 颗粒在滚筒内的混合过程
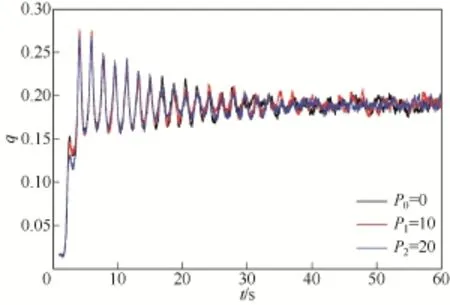
图6 3种工况下多粒径颗粒接触数变化
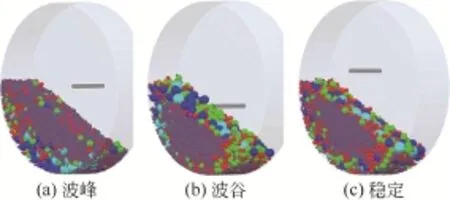
图7 大粒径颗粒分散过程
多粒径颗粒在滚筒内混合时,接触数的这种阻尼振动曲线变化不同于二元颗粒的接触数变化,阻尼振动曲线中接触数始终保持在某一值上下波动,趋势恒定,而二元颗粒的接触数[11]刚开始保持逐渐增大趋势,最后趋于稳定。阻尼振动曲线变化与多粒径颗粒在滚筒内的运动状态有关,大颗粒在最初混合时由堆积状态到逐渐分散需要一段过程,当堆积的大颗粒绝大部分处于平流层时,处于上面的1mm颗粒不断填充在大颗粒之间空隙中,增加了大颗粒与1mm颗粒之间的接触数,如图7(a),此时混合占据主导作用,接触数为波峰值;滚筒继续转动,大颗粒开始不断进入活动层,流动过程中的局部剪切作用使1mm颗粒通过大颗粒间隙下落,形成筛分分离,两者的接触数不断减小,当绝大部分大颗粒运动至活动层时,如图7(b),此时偏析占据主导作用,接触数也减小至波谷值。而在这个过程中,大颗粒逐渐分散,因此,每次的接触数波峰值会不断减小,波谷值不断增大,出现类似阻尼振动曲线变化的情况,直到混合达到稳定状态,大颗粒相对均匀的分散在活动层和平流层中,如图7(c)。
4 结论
(1)颗粒在非偏心滚筒内运动混合时,处于滚落运动模式的颗粒体系分为平流层、活动层和涡心3个区域。
(2)偏心滚筒内不存在实际的涡心;“移动涡心”随滚筒转动发生周期性变化,形状总是由小变大再逐渐变小的循环往复,位置总是向着靠近滚筒转轴的方向移动。
(3)非偏心滚筒内,大颗粒处于平流层时的匀速度在不同颗粒运动周期中基本相等;偏心滚筒内,大颗粒经历相邻两个运动周期的两次匀速度都不相等,且偏心距越大,匀速度的变化越明显。
(4)偏心距对滚筒内多粒径颗粒的接触影响较弱,而且多粒径颗粒在滚筒内混合时,接触数的变化类似阻尼振动曲线变化。
[1] 张立栋,李少华,余侃胜,等. 油页岩与固体热载体在回转干馏炉内混合特性的冷态实验[J]. 化工进展,2011,30(3):492-497. ZHANG L D,LI S H,YU K S,et al. Cold experiments on mixing performance of oil shale particle and solid heat carrier in rotary retorting[J]. Chemical Industry and Engineering Progress,2011,30(3):492-497.
[2] ISABEL F,VARGAS W L,MCCARTHY J J. Mixing and heat conduction in rotating tumblers[J]. Chemical Engineering Science,2010,65(2):1045-1054.
[3] HILL K M,KHAKHAR D V,GILCHRIST J F,et al. Segregation-driven organization in chaotic granular flows[J]. Proc. Natl. Acad. Sci.,1999,96(21):11701-11706.
[4] JAIN N,OTTINO J M,LUEPTOW R M. Combined size and density segregation and mixing in noncircular tumblers[J]. Phys.,2005,71(5):1-10.
[5] 王擎,肖冠华,孔祥钊,等. 固体热载体干馏桦甸油页岩试验研究[J]. 东北电力大学学报,2013,33(5):15-21. WANG Q,XIAO G H,KONG X Z,et al. Experimental investigation of solid heat carrier retorting of huadian oil shale[J]. Journal of Northeast Dianli University,2013,33(5):15-21.
[6] 陈辉,肖友刚,赵先琼,等. 回转窑内二元颗粒物料的径向混合[J]. 工程科学学报,2016,38(2):194-199. CHEN H,XIAO Y G,ZHAO X Q,et al. Transverse mixing of binary solid materials in a rotating kiln[J]. Chinese Journal of Engineering,2016,38(2):194-199.
[7] 欧阳鸿武,张新,黄誓成,等. 转鼓中颗粒流动层厚度及其影响因素[J]. 粉末冶金材料科学与工程,2008,13(2):84-90. OUYANG H W,ZHANG X,HUANG S C,et al. Thickness of granular flowing layer and its influencing factors in rotating drum[J]. Materials Science and Engineering of Powder Metallurgy,2008,13(2):84-90.
[8] JIANG M Q,ZHAO Y Z,LIU G S,et al. Enhancing mixing of particles by baffles in a rotating drum mixer[J]. Particuology,2011,9(3):270-278.
[9] 张立栋,李少华,朱明亮,等. 回转干馏炉内抄板形式与双组元颗粒混合过程冷模数值研究[J]. 中国电机工程学报,2012,32(11):72-78. ZHANG L D,LI S H,ZHU M L,et al. Cold mode numerical analysis of flights forms and two component particles mixing in rotary retorting[J]. Proceedings of the CSEE,2012,32(11):72-78.
[10] 张立栋,王丽伟,朱明亮,等. 回转干馏炉内油页岩与固体热载体颗粒轴向混合特性实验[J]. 东北电力大学学报,2012,32(6):63-66. ZHANG L D,WANG L W,ZHU M L,et al. Experimental on axis mixing degree of oil shale with solid heat carrier particles in rotary retorting[J]. Journal of Northeast Dianli University,2012,32(6):63-66.
[11] 李少华,王丽伟. 回转炉内壁炉型结构对颗粒混合效果的影响[J].煤炭学报,2013,38(10):1878-1881. LI S H,WANG L W. Effects of the particle mixed on furnace inner structure of rotary kiln[J]. Journal of China Coal Society,2013,38(10):1878-1881.
[12] 闫明,段文山,陈琼,等. 不同形状混合器中二元颗粒的分聚与混合研究[J]. 力学学报,2016,48(1):64-75. YAN M,DUAN W S,CHEN Q,et al. The segregation and mixing of binary granular systems in rotating mixer with different cross-sections[J]. Chinese Journal of Theoretical and Applied Mechanics,2016,48(1):64-75.
[13] AMARA A A,CARL D,DENIS R. Transverse mixing of polymer powders in a rotary cylinder part Ⅰ:Active layer characterization[J]. Powder Technology,2012,219(3):193-201.
[14] CHOU S H,HSIAU S S. Dynamic properties of immersed granular matter in different flow regimes in a rotating drum[J]. Powder Technology,2012,226(8):99-106.
[15] 赵永志,程易. 水平滚筒内二元颗粒体系径向分离模式的数值模拟研究[J]. 物理学报,2008,57(1):322-328. ZHAO Y Z,CHENG Y. Numerical simulation of radial segregation patterns of bina granular systems in a rotating horizontal drum[J]. Acta Physica Sinica,2008,57(1):322-328.
[16] GUPTA A,KATTERFELD A,SOETEMAN B,et al. Discrete element study mixing in an industrial sized mixer [DB/OL]. http://www. msm.ctw.utwente.nl/sluding/PAPERS/GuptaWCPT2010.pdf,2010:04-26.
[17] PUYVELDE D R V,YOUNGE B R,WILSON M A,et al. Experimental determination of transverse mixing kinetics in a rolling drum image analysis[J]. Powder Technology,1999,106(3):183-191.
[18] 张立栋,李连好,程硕,等. 颗粒在圆形偏心滚筒内的运动模式[J].化工进展,2015,34(9):3244-3247. ZHANG L D,LI L H,CHENG S,et al. Motion mode of particles in a circular eccentric drum[J]. Chemical Industry and Engineering Progress,2015,34(9):3244-3247
Research on motion and mixing of polydisperse particles in a circular eccentric drum
ZHANG Lidong,LI Lianhao,QIN Hong,WANG Qing
(Engineering Research Centre of Ministry of Education for Comprehensive Utilization of Oil Shale,Northeast Electric Power University,Jilin 132012,Jilin,China)
The discrete element method(DEM)was employed to simulate motion and mixing of polydisperse particles in a rotary drum. The effects of eccentricity on partition of particle system and its regional variation,change of large particle velocity and mixing degree of polydisperse particles were studied. Results showed that the rolling regime is divided three areas in the eccentric drum,particle system,the stagnant layer,the active layer and the vortex core. There is no actual vortex core,the shape and position of the "moving vortex core" are periodically changed with the rotation of the drum in the eccentric drum. In the center drum,the velocity of large particles in the stagnant layer is basically equal in different particle motion period. But in the eccentric drum,the two uniform velocity of the large particle in the two adjacent stagnant layer is unequal. The change of large particle velocity is more obvious with increasing eccentricity. The eccentricity has little effect on contact result of polydisperse particles. The variation of contact numbers of polydisperse particles is similar to that of the damping vibration curve in the mixing process.
discrete element method;eccentric drum;polydisperse particles;moving vortex core
TQ051
:A
:1000–6613(2017)02–0451–06
10.16085/j.issn.1000-6613.2017.02.007
2016-06-20;修改稿日期:2016-08-08。
教育部长江学者和创新团队发展计划(IRT13052)、吉林省自然科学基金(20150101033JC)、吉林市科技计划(201464044)及吉教科合字2015-237资助项目。
及联系人:张立栋(1980—),男,博士,副教授,主要研究方向为油页岩综合利用及回转装置混合与分离。E-mail:nedu1015@aliyun. com。

