气泡泵压降模型的分析与优化
谢育博,刘道平,杨亮,蒋丹清,杨梦
(上海理工大学新能源科学与工程研究所,上海200093)
气泡泵压降模型的分析与优化
谢育博,刘道平,杨亮,蒋丹清,杨梦
(上海理工大学新能源科学与工程研究所,上海200093)
利用两相流理论建立了一维、稳态的气泡泵压降数学模型。对3种均相流压降模型和15种分相流压降模型(3种分相流摩阻压降模型与5种截面含气率模型结合)进行了模拟计算,然后结合以饱和水为工质的气泡泵的实验数据,对理论值与实验值进行对比分析。结果表明:Friedel摩阻压降模型结合Zuber截面含气率模型的分相流压降模型的模拟精度最高,适用性最好。在选用该模型模拟气泡泵液体提升量随加热功率变化的流动特性时,发现理论值与实验值在一定加热功率范围内吻合很好,然而超过此范围,实验值与理论值的之差越来越大。因此提出了对气泡泵理论模型进行分段优化,结果表明:在低加热功率工况下模拟精度最高的是M-S分相流模型结合Tom变密度截面含气率模型,在高加热功率工况下模拟精度最高的是Dukler均相流摩阻压降模型。因此分段优化气泡泵理论模型的方法具有较高的可信性。
单压吸收式制冷;泵;两相流;模型;优化
气泡泵就是利用气泡“泵起”液体在系统中产生流体流动的输送装置。根据气体的来源不同,可以将泵分为两类:一种是输入式气泡泵,是指向装置底部输入外界气体,输入的气体和管内的液体形成上升的气液两相流,推动液体上升流动;另外一种是相变式气泡泵,是指加热泵内的液体,使液体发生相变产生蒸气,形成上升的气液两相流,从而达到推动液体上升的目的。气泡泵作为Einstein制冷循环[1]的核心部件,其效率对制冷循环的性能有重大影响。因此,对气泡泵性能参数的研究是单压吸收制冷系统的研究重点[2-3]。
20世纪50年代,在人们充分理解了两相流的基本理论后,STENNING和MARTIN[4]第一次使用两相流和动量平衡理论进行研究空气提升泵,利用气液的滑移率来关联气液两相特征进而研究在管径不变的条件下,改变沉浸比、气体流量时的液体提升量。DELANO[5]基于STENNING和MARTIN研究的空气提升泵设计了一个气泡泵模型,分析了热量输入、提升管直径、浸没比对气泡泵性能的影响。阙雄才等[6]基于系统的总压降平衡建立了绝热弹状流气泡泵的数学模型。在弹状流状态下,郑晓倩等[7]和陈永军[8]等分别进行了圆弧形导流式气泡泵的冷态试验研究和变截面直立管气泡泵理论模型的验证研究。刘振全等[9]应用气液两相流分相模型的压降理论,分析了气泡泵的压力特性,得出了相关的数学模型。平亚琴等[10]以分相流模型理论为基础,建立了气泡泵在绝热弹状流工况下的理论模型,并实验论证了该理论模型。陈永军等[11]基于漂移流模型理论,采用最小二乘法对气泡泵阻力系数进行拟合,完善了气泡泵理论模型。李华山等[12]也是基于两相漂移流模型理论,对以TFE/E181溶液为工质的扩散吸收式制冷系统气泡泵建立了数学模型,研究了提升管管径对有机工质气泡泵性能的影响分析。
气泡泵与环流式反应器流体力学特征的研究也有着相似之处。在研究环流式反应器的过程中,影响其性能的因素较多,并且各参数之间相互影响,导致放大很困难[13]。虽然已有许多经验、半经验关系式[14]估计反应器内的流体力学参数,但是不同的研究者采用不同的简化假设,适用范围非常窄,不具通用性。在前人研究的基础上,张立英等[15]指出在低气含率的情况下采用欧拉-拉格朗日法,在气含率和气泡数较大时,工程上多采用欧拉-欧拉两流体模型。因此在建立气泡泵压降模型的过程中,也可以借鉴环流式反应器流体力学的研究方法。因为现有的两相流压降模型大多也是基于一定实验条件的经验或者半经验公式,没有一个通用的两相流模型。因此有必要采用一定的模拟方法和评价标准,对建模过程中应用不同的两相流摩阻压降模型进行比较分析,选取出最优的适用于气泡泵的摩阻压降模型。
1 气泡泵压降模型
气泡泵如图1所示,系统主要包括竖直提升管、发生器、低位储液器和气液分离器四大部件。系统以饱和水为工质,运行在一个大气压下。定义气泡泵的提升管径为D,提升管长为L,气泡泵动力压头为H,气泡泵的沉浸比为H/L。

图1 气泡泵模型示意图
气泡泵压降包括水平管段单相流压降损失和提升管段两相流压降损失,基于两相流的基本压降理论和系统的压降平衡理论,应用气泡泵流动压头等于整个系统总压降,建立压降模型。
1.1 模型假设
气泡泵两相流复杂,为简化问题,作如下假设:
(1)垂直提升管内的两相流流动为稳定的一维两相绝热流动;
(2)储液器的液位稳定;
(3)气泡泵系统的散热忽略不计。
1.2 数学模型
气泡泵在稳态条件下,应用气泡泵流动压头等于整个系统的阻力损失,建立数学模型,见式(1)。

式中,流动动力为储液器自由液面的位能,即式(2)。

式中,Sf为流动压头;ρl为气泡泵内液体密度;H为相对液位高度。
工质循环过程中,压力降ΣΔP由储液器及连接管中的单相流压力降ΔP1和发生器及提升管中的两相流压力降ΔP2组成。
根据流体静力学定常不可压缩流动的基本理论,单相流体从低位储液器到发生器整个流道所产生的阻力包括沿程摩擦阻力和局部阻力损失,见式(3)。
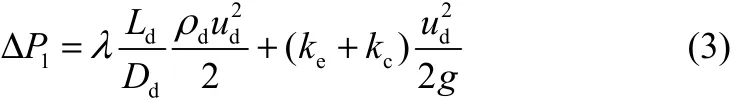
式中,λ为整个连接管的沿程损失系数,层流状态下的λ=64/Re;ρd为连接管内单相流体的密度,ρd=ρl;ke为连接管的进口损失系数,ke=0.5;kc为连接管的出口损失系数,kc=1;Ld、Dd分别为中间连接管的长度和直径;ud为连接管内单相流体流速。两相流压降由提升管入口处的局部阻力压降和提升管中的压降组成,见式(4)。

式中,ΔPTPE为竖直提升管局部压力损失;ΔPTPF为竖直提升管压降。
由于气泡泵系统中带有气泡收集器,所以从低位储液器中生成的饱和水蒸气和饱和水进入气泡泵提升管口时将产生局部阻力损失。此时的局部阻力损失按照单相流的突缩接头来处理:气体单独流经气泡收集装置中产生的局部压降ΔPjg与液体流入提升管的局部压降之和ΔPjl,见式(5)~式(7)。
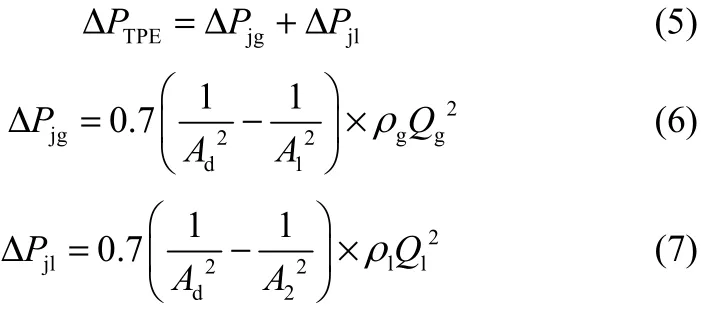
式中,Ad为气泡收集器上端口横截面积;A1为气泡收集器下端口的截面积;A2为发生器的横截面积;Ql为液体提升量;Qg为气体流量。
提升管中的压降由摩擦压降ΔPf、重力压降ΔPg、加速压降ΔPm组成,即式(8)。
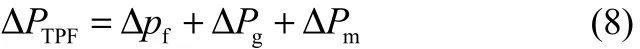
重力压降ΔPg见式(9)。
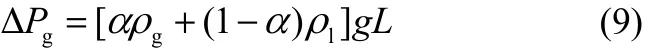
式中,ρg为气体密度;L为提升管管长;α为截面含气率。
截面含气率α是气液两相流的基本参数之一,然而它不可以直接被测量,并且变化率较,很难用热力学方程来计算,为了求得截面含气率的准确值,许多学者进行了大量的实验研究[16-17],并提出了各种计算模型(Mponqjibcrnn滑速比模型、Smith混合相-单相模型、Tom变密度模型、Zivi最小熵增模型和Zuber漂移流模型)。
加速压降ΔPm影响较小,可按分相流加速压降处理可得,见式(10)。
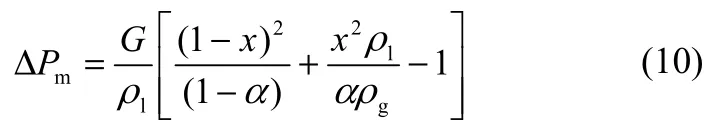
常用的摩擦压降计算模型包括均相流摩阻压降模型和分相流摩阻压降模型。本文选用了3种典型的均相流模型(Mecadam、Dukler和Cicchitti)和3种分相流模型(L-M模型[18]、Friedel模型[19]和M-S模型[20])进行评价,分析各模型在气泡泵中的适用性。
2 两相流摩阻压降模拟结果分析
2.1 均相流摩阻压降模拟结果分析
选取测量精细、可靠性较高的平亚琴等[10]实验数据进行分析。其具体的实验工况如下:系统压力为一个大气压,工质为水,管径为16mm,长为600mm,加热功率为12个测量点(150W、175W、200W、225W、250W、275W、300W、325W、350W、375W、400W、450W),沉浸比为0.25、0.3、0.35、0.4、0.45,在模拟计算中,将气泡泵沉浸比和加热功率作为变量,共计60个工况点。应用上述3种均相流黏度模型计算各个工况下的质量流量,并将理论值与实验值进行比较。
图2为各个均相流摩阻压降模型模拟评价结果,用不同颜色的柱状图表示不同的模型。从图2(a)中可以看出Cicchitti模型的值最小,说明其具有最高的模拟精度,从图2(b)中可以看出各个均相流摩阻压降模型的模拟值波动不大,因此综合考虑推荐使用Cicchitti均相流摩阻压降模型。
2.2 分相流摩阻压降模拟结果分析
图3为3种分相流摩阻压降模型和与之匹配的5种截面含气率模型的模拟结果,用不同颜色的柱形图表示不同的截面含气率模型。
分析图3(a),在截面含气率相同时,Fridel分相流模型的模拟精度最高;在摩阻压降模型相同时,Zuber漂移流截面含气率模型的模拟精度最高。从图3(b)中可以看到,Fridel摩阻压降模型结合Zuber漂移流截面含气率模型的标准差最小,计算稳定性最好。这是由于Friedel摩阻压降模型基于大量实验数据并且考虑了重力和表面张力的影响,Zuber漂移流截面含气率模型既考虑了两相的流速和空泡份额的不均匀性,又考虑了气液相间的相对速度,因而是一种较好的计算截面含气率的方法,有较大的适用性。因此,在进行全局气泡泵压降理论模型建立时,推荐使用Fridel分相流摩阻压降模型和Zuber漂移流截面含气率模型相结合。
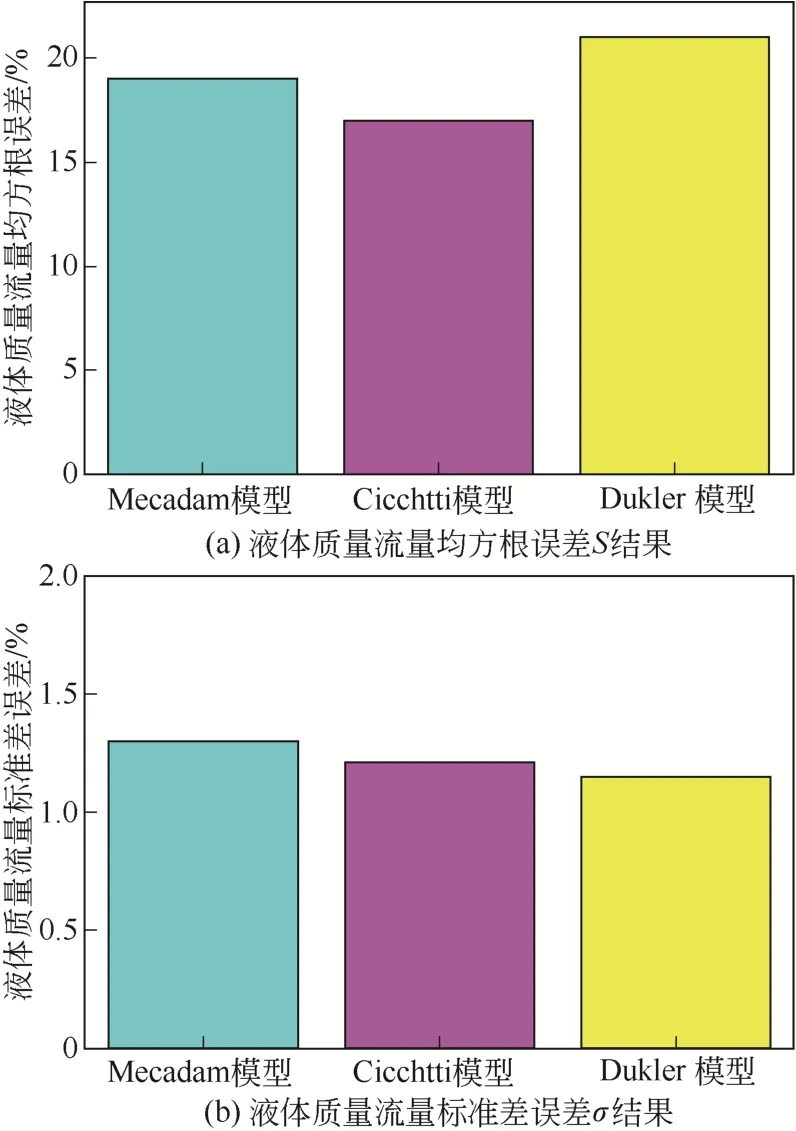
图2 均相流摩阻压降模型的模拟评价结果
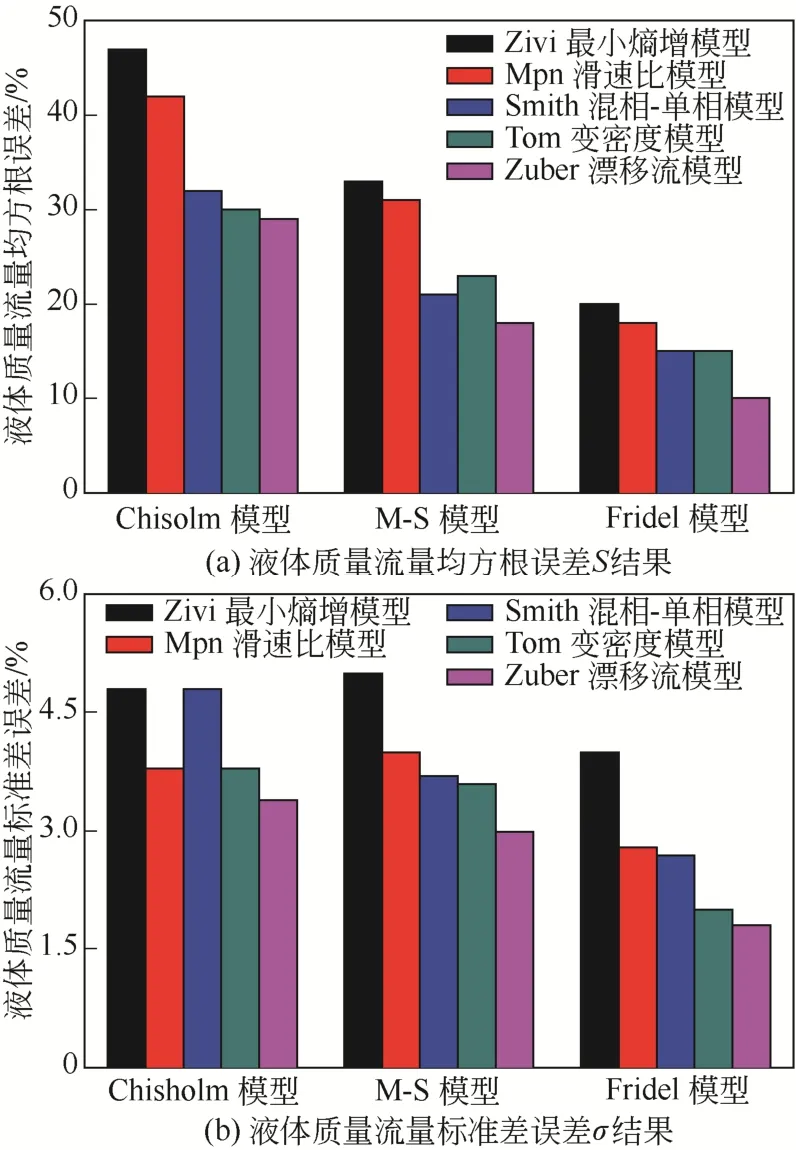
图3 分相流摩阻压降模型的模拟评价结果
3 气泡泵两相流摩阻压降模型优化
当选用上述模型来模拟气泡泵内液体随加热功率变化的流动特性时,发现理论值与实验值在一定加热功率范围内吻合很好,但是超过此范围,实验值与理论值的曲线分离度越来越大,如图4所示。当加热功率约为250W时,流型开始发生转变,此点为临界点。因此提出了分段建立理论模型的优化方法,以实验液体提升速度拐点为分界点,分别对低加热功率工况和高加热功率工况选出各段的最优模型,从而进一步优化气泡泵压降理论模型。
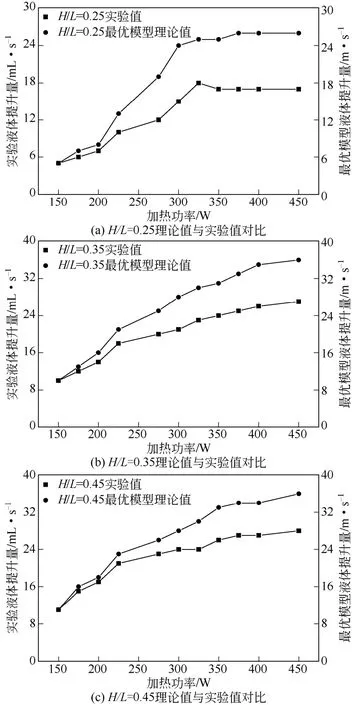
图4 不同沉浸比下气泡泵理论值与实验值的对比
3.1 低加热功率工况点下理论模型优化分析
3.1.1 均相流摩阻压降模型优化分析
图5为低加热功率下的各个均相流摩阻压降模型模拟评价结果。从图5中可以看出,各个均相流摩阻压降模型的液体质量流量均方根误差S值相差不大,但是液体质量流量标准差σ值相差较大,Dukler模型的值最小。因此推荐使用Dukler均相流摩阻压降模型。
3.1.2 分相流摩阻压降模型优化分析
图6为低加热功率工况下的各个分相流摩阻压降模型的模拟评价结果。在分析均方根误差和标准误差时可以发现:在截面含气率相同时,M-S分相流模型的模拟精度最高;在摩阻压降模型相同时,Tom截面含气率模型的模拟精度最高。因此综合考虑推荐M-S摩阻压降模型结合Tom变密度截面含气率模型。
从图7中可以看到,在低加热功率时左侧管子和3根管子的上部会出现泡状流,右两根管子的底部和中部有较小的弹状流。结合上述模拟分析的结果,推荐使用M-S摩阻压降模型结合Tom变密度截面含气率模型。这是由于M-S模型在湍流区适用性较好,气泡泵工作时两相流处于湍流区,所以匹配度高;Tom变密度模型适用于泡状流流型,最初气泡泵的流型为泡状流,因而是一种较好的计算截面含气率的方法,有较大的适用性。
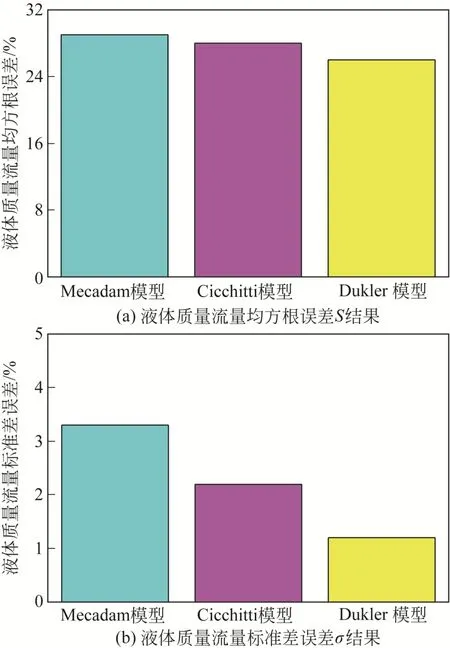
图5 低加热功率下均相流摩阻压降模型的模拟评价结果
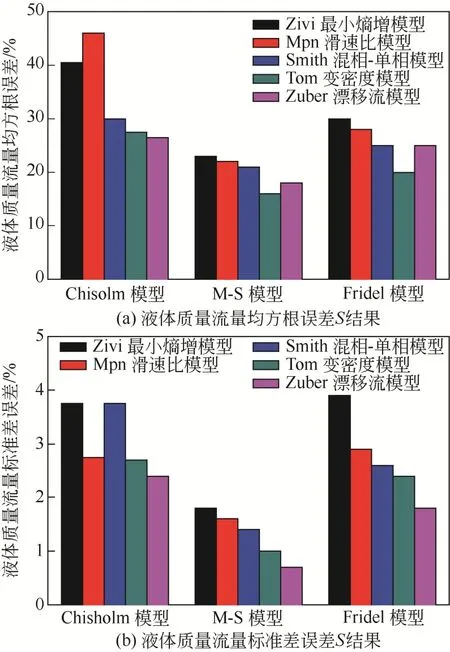
图6 低加热功率下分相流摩阻压降模型的模拟评价结果

图7 加热功率225W的流动形态
3.2 高加热功率工况点下理论模型优化分析
3.2.1 均相流摩阻压降模型优化分析
图8为高加热功率下的各个均相流摩阻压降模型的模拟评价结果。从图8中可以看出,Dukler均相流摩阻压降模型的液体质量流量均方根误差S值和标准差σ值均是最小的,说明Dukler均相流摩阻压降模型模拟结果是比较接近实验值的。因此推荐使用Dukler均相流摩阻压降模型。
3.2.2 分相流摩阻压降模型优化分析
图9为高加热功率下的各个分相流模型的模拟评价结果。当采用相同的截面含气率模型时,Friedel分相流模型具有最高的模拟精度;在摩阻压降模型相同时,Smith混相-单相截面含气率模型具有最高的模拟精度,计算稳定性最好。因此,综合考虑推荐使用Friedel模型结合Smith混相-单相截面含气率模型。
从图10中可以看到,在高加热功率为400W时管内出现弹状流——环状流。对比均相流模型模拟结果和分相流模型结合Smith混相——单相截面含气率模型的模拟结果,可以发现均相流模型的均方根误差和标准差误差的值均比分相流模型的模拟值小。其原因是均相流模型适用于高质量流速的流动,而在气泡泵中,随着加热功率的增加,竖直提升管内气液两相流流型发生变化,从泡状流到弹状流甚至出现环状流,当处于弹状流状态或者环状流状态时液体质量流速高,所以模型匹配度好。因此,在高加热功率的工况下,推荐使用Dukler均相流摩阻压降模型。
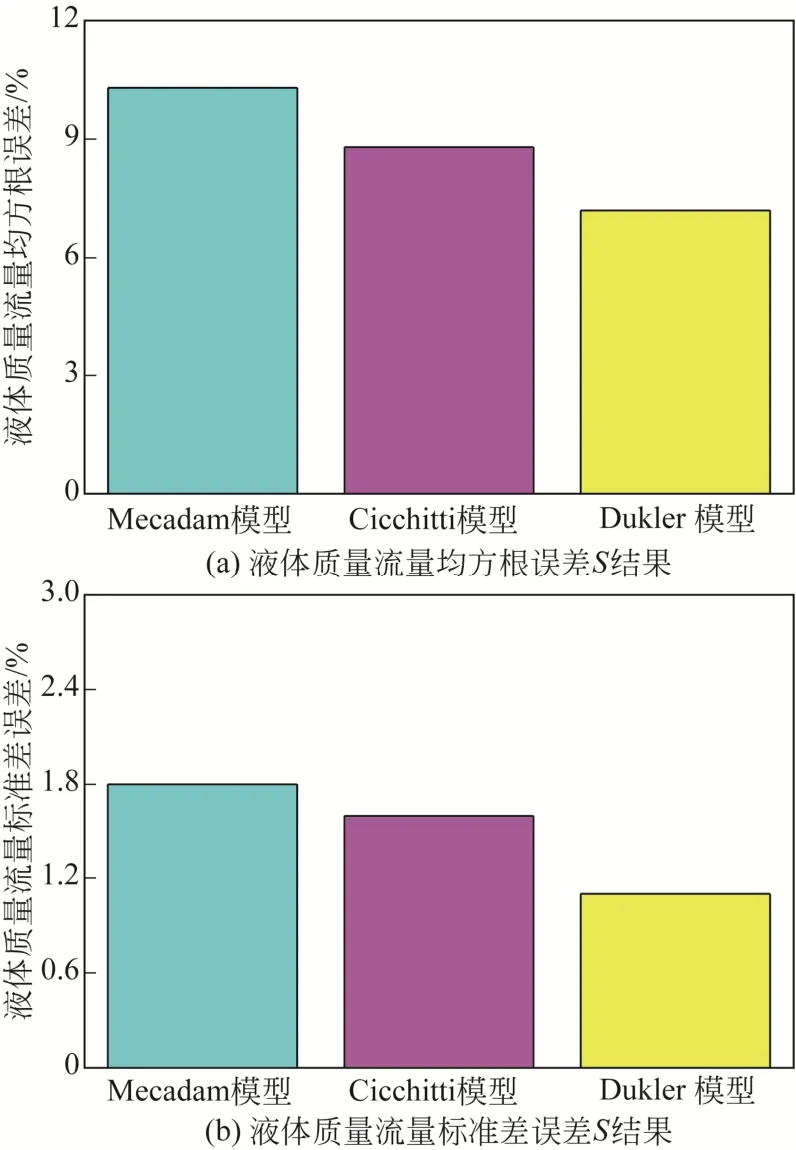
图8 高加热功率下均相流摩阻压降模型的模拟评价结果
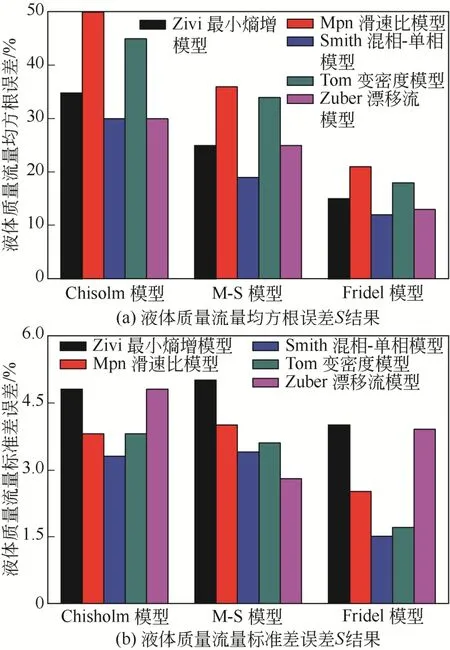
图9 高加热功率下分相流摩阻压降模型的模拟评价结果

图10 加热功率400W的流动形态
3.3 优化模型的验证
根据上述结果,在低加热功率工况下选用M-S分相流模型结合Tom变密度截面含气率模型;在高加热功率工况下选用Dukler均相流摩阻压降模型,进行模拟计算沉浸比H/L为0.25、0.35、0.45工况下的理论值,并与全局最优理论值和实验值进行对比,如图11所示。
从图11中可以看出,分段优化模型的曲线更加接近实验值并且曲线变化趋势一致,结果表明:分段优化气泡泵压降理论模型的方法具有高的可信性。
4 结论
本文利用两相流理论建立一维、稳态的压降数学模型,结合已有的实验数据,选取3种均相流模型和15种分相流压降模型(3种分相流摩阻压降模型结合5种截面含气率模型)进行模拟,并分析评价每种模型的优劣性,进而优化压降模型,现得出如下结论。
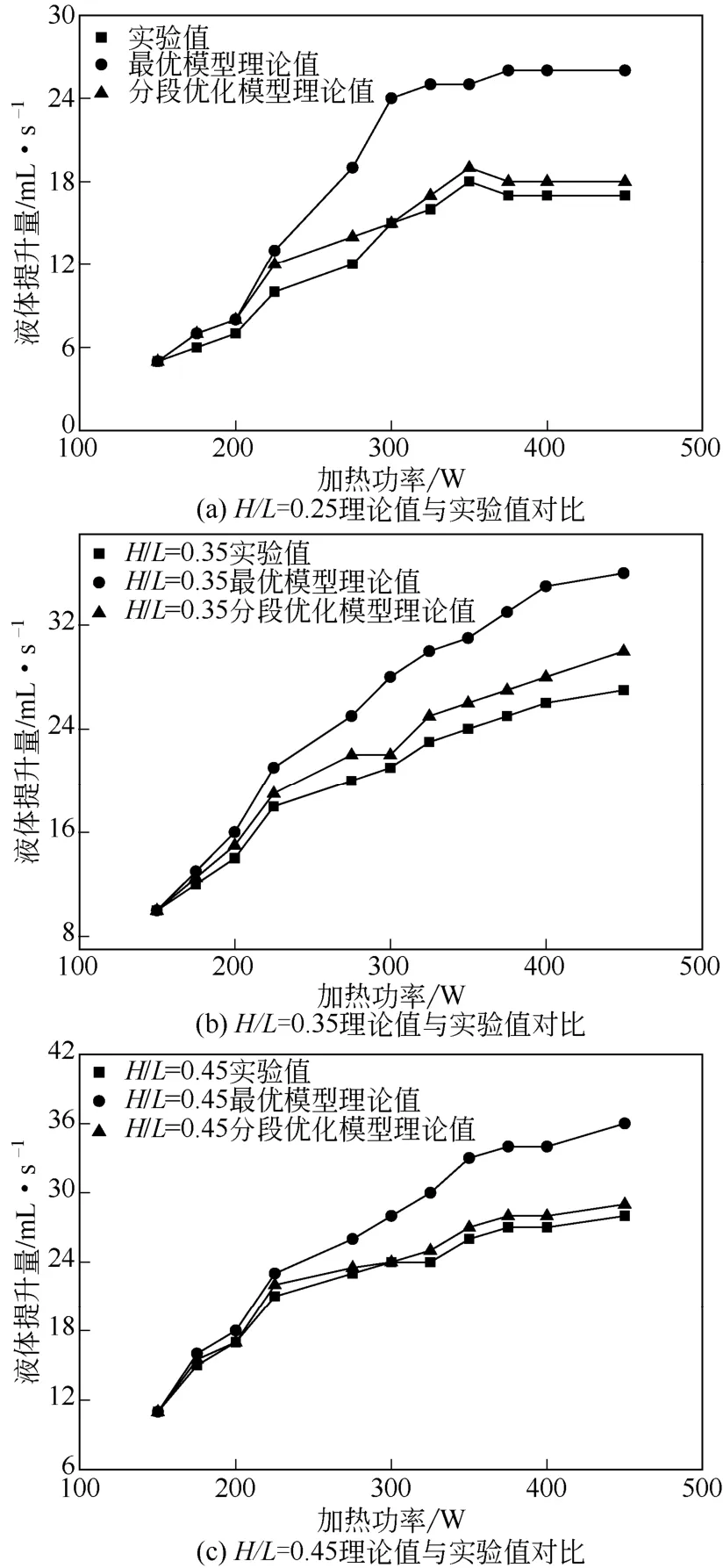
图11 不同沉浸比下分段优化模型的验证
(1)在不同加热功率工况下只选用一种摩阻压降模型时,模拟结果表明,Fridel分相流模型结合Zuber漂移流截面含气率模型的模拟精度最好,对于气泡泵的适用性最好。
(2)选用Fridel分相流模型结合Zuber漂移流截面含气率模型的计算结果与实验值比较时,发现理论值与实验值在一定加热功率范围内吻合很好,超过此范围,实验值与理论值的曲线分离度越来越大。所以提出了分段优化模型的方法。
(3)根据加热功率的大小,进行分段优化气泡泵理论模型。在低加热功率工况下,选用M-S分相流模型结合Tom变密度截面含气率模型;在高加热功率工况下选用 Dukler均相流模型。实验结果表明分段优化模型的理论计算值与实验值具有较高的吻合度。因此分段优化气泡泵理论模型的方法具有很高的可信性。
符号说明
Ad——气泡收集器上端口的截面积,m2
Al——气泡收集器下端口的截面积,m2
D——提升管径,m
Ds——中间连接管的直径,m
H——低位储液器的相对高度,m
H/L——沉浸比
kd——出口损失系数
ke——进口损失系数
L——提升管长,m
Ls——中间连接管的长度,m
ΔPf——摩擦压降,Pa
ΔPg——重力压降,Pa
ΔPjg——气体单独流经气泡收集装置中产生的局部压降,Pa
ΔPjl——液体流入提升管的局部压降之和,Pa
ΔPm——加速压降,Pa
ΔPTPE——竖直提升管局部阻力降,Pa
ΔPTPF——竖直提升管压力降,Pa
Qg——气体流量,m3/s
Ql——液体提升量,m3/s
S——均方根误差
Sflow——流动压头,Pa
us——为连接管内单相流体流速,m/s
α——截面含气率
λ——沿程损失系数
ρg——气体密度,kg/m3
ρl——液体密度,kg/m3
ρs——为单相流体的密度,kg/m3
σ——标准差
[1] EINSTEIN A,SZILARD L.The Einstein-Szilard refrigerator:US1781541[P].1930-11-11.
[2] 方甲闯,郑宏飞,李正良.小型太阳能吸收式空调多根弦月形通道溶液提升泵的性能研究[J].太阳能学报,2007,28(3):291-295.FANG Jiachuang,ZHENG Hongfei,LI Zhengliang. Study on performance of the thermosiphon solution elevation pump with multi-lunate channels in minitype solar absorption type air-conditioning system[J].Acta Energiae Solaris Sinica,2007,28(3):291-295.
[3] 汤成伟,刘道平,祁影霞,等.单压吸收式Enistein循环制冷机中气泡泵的性能分析[J].制冷学报,2009,30(3):35-39.TANG Chengwei,LIU Daoping,QI Yingxia,et al. Performance of bubble pump in single-pressure Einstein absorption refrigerator [J].Journal of Refrigeration,2009,30(3):35-39.
[4] STENNING A H,MARTIN C B. An analytical and experimental study of air lift pump performance[J]. Eng.Power,Trans.ASME,1968,90:106-110.
[5] DELANO A.Design Analysis of the Einstein Refrigeration cycle[D].Atlanta,Georgia:Georgia Institute of Technology,1998.
[6] 阙雄才,李红.热虹吸泵绝热弹状流的热虹吸特性研究——无泵溴化锂吸收式太阳能制冷机机理研究之二[J].太阳能学报,1989,10(1):1-13.QUE Xiongcai,LI Hong. Study on thermal siphon characteristics of slug flow with heat insulation in thermal siphon pump——the second mechanism studies on pumpless LiBr absorption solar refrigerating machine[J].Acta Energiae Solaris Sinica,1989,10(1):1-13.
[7] 郑晓倩,刘道平,陈永军,等.圆弧形导流式气泡泵的冷态试验研究[J]. 流体机械,2015(9):58-62.DENG Xiaoqian,LIU Daoping,CHEN Yongjun,et al.Experimental study of circular arc form guided bubble pump under cold state[J].Fluid Machinery,2015(9):58-62.
[8] 陈永军,刘道平,黄塬琳,等.变截面直立管气泡泵理论模型验证研究[J]. 太阳能学报,2016(4):917-923.CHEN Yongjun,LIU Daoping,HUANG Yuanlin,et al.Theoretical model validation study of variable cross-section upright tubular bubble pump[J].Acta Energiae Solaris Sinica,2016(4):917-923.
[9] 刘振全,吴玉莹,张中诚.无泵溴化锂吸收式制冷气泡泵压力特性数学模型的探讨[J].兰州理工大学学报,2003,29(4):57-59.LIU Zhenquan,WU Yuying,ZHANG Zhongcheng.Inquiry of mathematical model for pressure characteristics of bubble pump for pump-free lithium bromide absorption refrigeration[J].Journal of Gansu University of Technology,2003,29(4):57-59.
[10] 平亚琴,刘道平,陈盛祥,等. 单压吸收式制冷系统气泡泵理论模型与实验研究[J]. 制冷学报,2010,31(6):46-50.PING Yaqin,LIU Daoping,CHEN Shengxiang,et al. Theoretical model and experimental analysis of bubble pump in single-pressure absorption refrigeration system[J]. Journal of Refrigeration,2010,31(6):46-50.
[11] 陈永军,刘道平,黄塬琳,等. Einstein 制冷系统气泡泵理论模型修正验证研究[J]. 制冷学报,2014(6):68-74.CHEN Yongjun,LIU Daoping,HUANG Yuanlin,et al.Correction and validation of theoretical model of bubble pump in einstein refrigeration system[J]. Journal of Refrigeration,2014(6):68-74.
[12] 李华山,王令宝,卜宪标,等.提升管管径对有机工质气泡泵性能的影响分析[J]. 新能源进展,2016,4(1):56-61.LI Huashan,WANG Lingbao,BU Xianming,et al. Effects of lift-tube diameter on performance of bubble pump with organic working fluids[J].Advances in New and Renewable Energy,2016,4(1):56-61.
[13] ROBERT F,MUDDE. Gravity-driven bubbly flows[J]. Annual Review of Fluid Mechanics,2005,37(1):393-423.
[14] ZHANG T,WANG J,LUO Z,et al. Multiphase flow characteristics of a novel internal-loop airlift reactor[J]. Chemical Engineering Journal,2005,109(1):115-122.
[15] 张立英,黄青山. 气升式环流反应器的理论研究进展[J]. 过程工程学报,2011,11(1):162-173.ZHANG Liying,HUANG Qingsan.Research progress in the modeling theory of airlift loop reactor[J].The Chinese Journal of Process Engineering,2011,11(1):162-173.
[16] MÜLLER-STEINHAGEN H,HECK K.A simple friction pressure drop correlation for two-phase flow in pipes[J]. Chemical Engineering and Processing:Process Intensification,1986,20(6):297-308.
[17] LOMBARDI C,CARSANA C.Dimensionless pressure drop correlation for two-phase mixtures flowing up-flow in vertical ducts covering wide parameter ranges[J].Heat and Technology,1992,10(1):125-141.
[18] LOCKHART R,MARTINELLI R. Proposed correlation of data for isothermal two-phase,two-component flow in pipes[J]. Chemical Engineering Progress,1949,45(1):39-48.
[19] FRIEDEL L.Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow[C]//European Two-Phase Flow Group Meeting,1979.
[20] 林宗虎.气液两相流和沸腾传热[M].西安:西安交通大学出版社,2003.LIN Zonghu.Gas liquid two phase flow and boiling heat transfer[M].Xi’an:Xi’an Jiaotong University Press,2003.
Analysis and optimization of bubble pump pressure drop model
XIE Yubo,LIU Daoping,YANG Liang,JIANG Danqing,YANG Meng
(Institute of New Energy Science and Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
Two-phase flow theory was used to establish an one-dimensional and steady state mathematical model of bubble pump pressure drop. Three kinds of homogeneous flow pressure drop models and 15 kinds of split phase flow pressure drop models (three kinds of split phase flow friction pressure drop models with 5 kinds of cross section gas rate models) were selected to simulate,then the experimental data of the bubble pump with saturated water as working fluid were analyzed and compared with the theoretical value. The result showed that simulation accuracy of the Friedel friction pressure drop model combining Zuber section gas rate model is the highest. However,when we use this model to simulate the flow characteristics of the liquid lift of the bubble pump with the change of the heating power,we found that the theoretical value and the experimental value agree well only within a certain range of heating power. Therefore,sectional optimization on bubble pump model was put forward. We found that the simulation accuracy of M-S split phase flow model combined with Tom variable density section gas rate model is the highest under the working condition of low heating power. The Dukler homogeneous flow model of the friction pressure drop is the best model under the higher heating power working condition. Therefore,the method of optimizing the theoretical model of bubble pump by subsection has high credibility.
single-pressure absorption refrigeration;pump;two-phase flow;model;optimization
TH3
:A
:1000–6613(2017)02–0418–08
10.16085/j.issn.1000-6613.2017.02.003
2016-06-06;修改稿日期:2016-09-01。
上海市研究生创新基金(JWCXSL1302)及上海市教育委员会科研创新项目(13ZZ117)。
谢育博(1991—),男,硕士研究生。联系人:刘道平,教授。E-mail:dpliu@usst.edu.cn。

