轨道交通线网常乘客比例分析

鲍 枫，汪 波,3，黄建玲，何志莹

（1.北京市交通信息中心，北京市 1 00161；2.综合交通运行监测与服务北京市重点实验室，北京市 1 00161；3.北京市交通委员会，北京市 1 00161）

轨道交通线网常乘客比例分析

鲍 枫1,2，汪 波1,2,3，黄建玲1,2，何志莹1,2

（1.北京市交通信息中心，北京市 1 00161；2.综合交通运行监测与服务北京市重点实验室，北京市 1 00161；3.北京市交通委员会，北京市 1 00161）

根据城市轨道交通常乘客比例数据的节假日特点，在消除常乘客比例数据的趋势项的时候，引入表示节假日特征的虚拟变量，量化节假日因素对常乘客比例的影响，建立常乘客比例数据与时间、具有节假日特征的虚拟变量之间的回归模型,达到同时消除趋势项和节假日特征的影响的目的，掌握节假日对常乘客比例的影响规律。通过自相关和偏自相关函数对消除趋势项和节假日因素的数据序列进行平稳性和周期性分析，消除周期性特征影响。最后，构建基于虚拟变量线性回归和季节ARIMA的组合预测模型，修正了原有的季节ARIMA。以2015年3月2日到2016年3月27日之间56周的北京轨道交通日常乘客比例数据进行实例验证，表明本文构建的组合预测模型的精度高于原有的季节ARIMA模型。

轨道交通；常乘客比例；虚拟变量；回归模型；修正季节ARIMA模型

0 引 言

城市轨道交通具有大容量、快速准点、安全高效等优点，近年来客流量增长迅猛，使得轨道交通面临着严重的拥挤问题，这给有关部门的运营组织管理工作提出了新的课题。鲁放等[1]提出轨道交通常乘客的概念，定义为“经常乘坐城市轨道交通出行，并熟练使用城市轨道交通，而且具备一定出行习惯的乘客”。常乘客的比例会受到假期、季节等因素的影响。本文以城市轨道交通一卡通使用量比例表征轨道交通线网常乘客比例，建立轨道交通线网常乘客比例预测模型，研究常乘客的比例变化趋势，为轨道交通运营组织提供参考，提升轨道交通运输服务水平。

统计期内的轨道交通常乘客比例是按照时间顺序取得的一系列轨道交通常乘客比例观测值。这些观测值形成时间序列。基于时间序列的预测理论的基本思想是时间序列的任一时刻的值与其前期数据相关。通过建立这种相关关系的模型在历史数据的基础上预测将来的未知数据[2-4]。现实中的数据很多是非平稳的时间序列，如股价序列、气候变化等，George E.P.Box和 Gwilym M.Jenkins提出自回归整合滑动平均模型(ARIMA)能解决非平稳时间序列的处理问题。

在这种非平稳的时间序列中，有些序列存在明显的周期性变化。这种周期是由于季节性变化（包括季度、月度、周度等变化）或其他一些固有因素引起的。这类序列称为季节性序列，如季度时间序列、月度时间序列、周度时间序列等。处理季节性时间序列只用以上介绍的方法是不够的。描述这类序列的模型之一是季节时间序列模型(seasonal ARIMA model)用SARIMA表示，较早文献也称其为乘积季节模型（multiplicative seasonal model）。居民季度用煤消耗量、某地区的月降水量、居民日用水量、轨道交通日客运量、轨道交通日常乘客比例等属于季节性时间序列。国内已经有很多文献探讨了季节ARIMA模型在各行业的应用[5-8]。蔡昌俊等[9]基于城市轨道交通自动售检票系统采集的进出站客流的历史数据，构建了乘积ARIMA模型，实现对进出站客流量的精确预测；何九冉[10]构建了城市轨道交通某运营线路平常日客流预测ARIMA-RBF组合模型。

除了利用ARIMA模型及组合模型研究轨道交通客流规律，李春晓等[11]提出一种基于广义动态模糊神经网络（GD-FNN）的短时进站客流量预测方法，预测轨道交通车站每日分时进站量；王玉萍等[12]提出了包含可信度分析、客流特性分析、风险性分析和敏感性分析在内的城市轨道交通客流预测结果分析的结构体系；郝勇[13]构建了周客流日均量的回归模型，测算上海地铁周客流日均量趋势值；徐瑞华等[14]研究了城市轨道交通线路客流分布的实时预测方法。但是在目前的研究中，时间序列的取值会受到节假日，例如元旦、春节、五一等的影响，如果只是使用差分方法，去除不了节假日的影响。

基于以上现状，本文通过分析2015年3月2日到2016年3月27日之间56周的北京轨道交通日常乘客比例数据，引入表示节假日特征的虚拟变量，通过建立回归方程的形式，去除趋势项和节假日影响因素，建立城市轨道交通常乘客比例修正季节ARIMA模型，掌握常乘客比例随日期及节假日变化的规律，预测短期内常乘客比例。

1 修正季节ARIMA模型构建

一般季节ARIMA模型通过逐步消除趋势项、季节项，然后对得到的平稳序列建立ARMA预测模型。但是在日时间序列数据中，数据值还会受到节假日的影响，例如元旦、春节、五一等，通过传统的差分方法消除不了节假日的影响。本文提出引入表示节假日特征的虚拟变量，建立基于虚拟变量的线性回归模型来消除趋势项和节假日的影响，对来消除趋势项和节假日的影响之后的序列再构建季节ARIMA模型，最后得到基于虚拟变量线性回归和季节ARIMA的组合预测模型，对原有的季节ARIMA模型进行修正。这种方法不需要人为的事先去除节假日的数据，避免了缺失信息的产生，保证了数据信息的连续性，同时有利于掌握节假日对常乘客比例的影响规律。具体步骤：

第一步：建立城市轨道交通常乘客比例数据与连续变量和具有节假日特征的虚拟变量的回归模型，见式（1）：

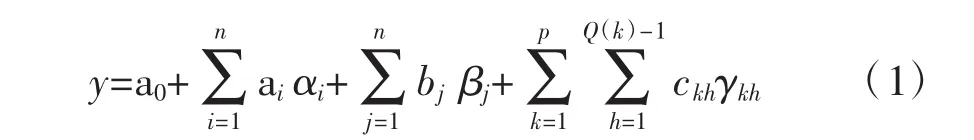
式中：y为城市轨道交通常乘客比例数据；a0为常数项；αi为第i个连续变量；ai为第i个连续变量的系数；n为连续变量的个数；βj为第j个节假日特征有序虚拟变量；bj为第j个节假日特征有序虚拟变量的系数；m为节假日特征有序虚拟变量的个数；γkh为第k个节假日特征无序虚拟变量的第h个哑元变量，如果某一节假日特征取值有Q（k）种情况，并且是无序的，应引入Q（k)-1个表示这一特征的哑元变量；ckh为第k个节假日特征无序虚拟变量的第h个哑元变量的系数；Q（k）为第k个节假日特征无序虚拟变量的取值个数；P为节假日特征无序虚拟变量的个数。

第二步：进行m个节假日特征有序虚拟变量与p个节假日无序特征变量（γ11，γ12，…，γ1，Q(1)-1），（γ21，γ22，…，γ2,Q(2)-1）…，（γp1，γp2，…，γp,Q(p）-1）相互之间相关关系的检验，得到分别独立的节假日特征虚拟变量的组合。

第三步：y分别与第二步得到的独立的节假日特征虚拟变量的组合建立回归方程，应用最小二乘法得到参数组合，根据t检验、修正的R2、AIC、SC等检验规则，确定最优回归方程，从而确定a0、ai、bj、ckh等系数的估计值、、、，并对y进行预测，得到y的预测值，见式（2）：

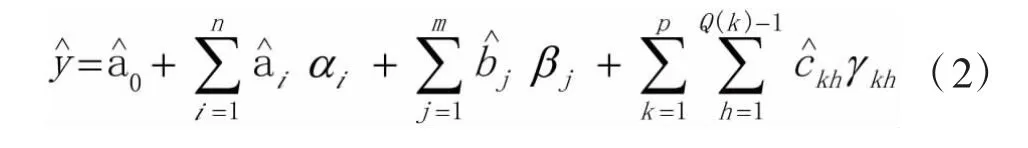
式中：P为季节自回归阶数；Q为季节移动平均阶数；ΦP（BS）为季节P阶自回归算子；ΘQ（BS）为Q阶移动平均算子。

第五步：结合式（2）和式（3），建立城市轨道交通常乘客比例数据组合预测模型，见式（4）：

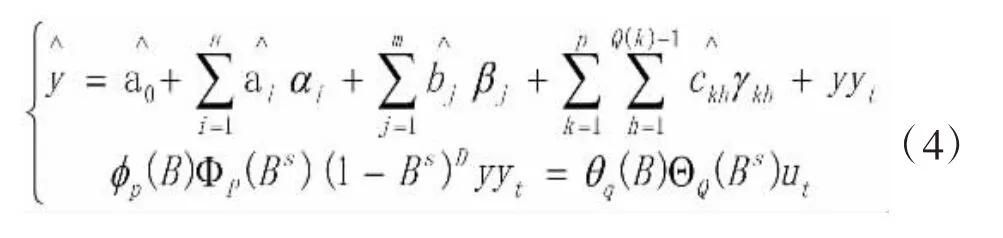
2 实例验证

本节中，使用季节ARIMA方法（方法一）及修正后的基于虚拟变量线性回归和季节ARIMA的组合预测模型（方法二，式（4））对城市轨道交通常乘客比例数据进行建模，并对比两种方法的精确度，数据时间段为2015年3月2日到2016年3月27日之间56周的北京城市轨道交通常乘客比例数据，共392个数据。

2.1 季节ARIMA方法（方法一）

根据北京城市轨道交通常乘客比例数据的特征，建立ARIMA(2,1,3)(1,1,1)7的模型。模型展开式见式（5）：

利用式（5）预测2016年3月28日至4月4日（4月2日至4月4日为清明节假期）的日常乘客比例，结果见表1。

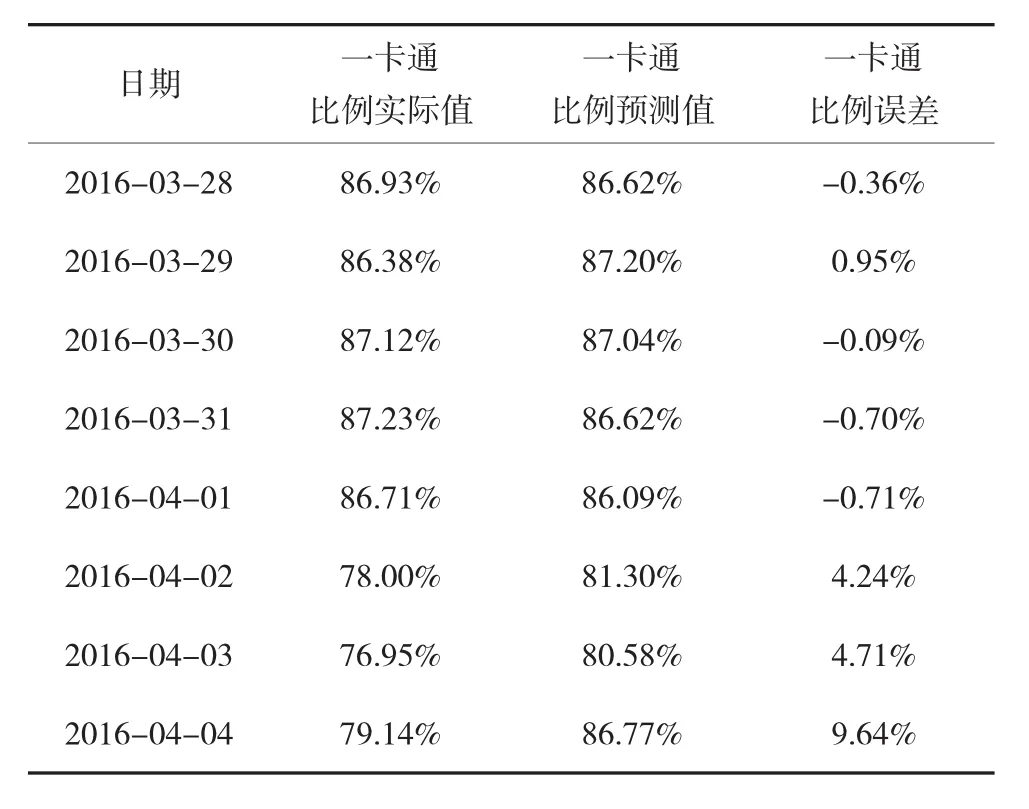
表1 方法一预测结果及误差

2.2 基于虚拟变量线性回归和季节ARIMA的组合预测模型（方法二，修正季节ARIMA模型）

2.2.1 模型建立

按照第1节描述的方法进行建模，引入表征节假日特征的有序和无序虚拟变量：

（1）表征节假日长短的虚拟变量β1：此虚拟变量为有序分类变量，所以取值用0，1，2来表示。0表示非节假日；1表示长度为3天的节假日，例如元旦、清明、五一、端午、元宵节；2表示长度为7天的节假日，例如春节、十一。

（2）表征节假日的回家、旅游特征变量γ11，γ12:此变量为无序变量，特征取值为回家、旅游及非节假日，所以需生成两个哑变量γ11，γ12。在我国节假日中，春节、清明一般外地人回老家比较多，赋值为γ11=1，γ12=0；其他节假日旅游特征赋值为γ11=0，γ12=1；非节假日赋值为γ11=0，γ12=0。

（3）表征不同节假日的虚拟变量：每年节假日有7种，分别为元旦、春节、清明、五一、端午、元宵节、十一，但是有时会因为一些原因增加放假日期，例如2015年9月3日至5日调休放假，形成3天小长假，所以认为节假日有8种,分别为元旦、春节、清明、五一、端午、中秋节、十一、其他，再加上还需赋值非节假日，所以节假日种类有9种。节假日为无序变量，量化时需派生出8个哑变量，取值见表2。

根据修正的决定系数（Adjusted R2）、AIC、SC等检验规则，表征节假日长短虚拟变量β1与城市轨道交通常乘客比例时间序列数据建立回归方程为最优方案。回归方程为式（6）：

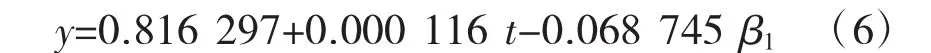
从式（6）可得出：节假日的长短对轨道交通日常乘客比例数据有明显的影响，长度为7天的节假日常乘客比例值平均比长度为3天的节假日常乘客比例值低0.069左右。

记利用式（6）消除趋势项和节假日影响后的数据序列为yy，对yy建立ARIMA（2,0,3）（1,1,1）7的模型。

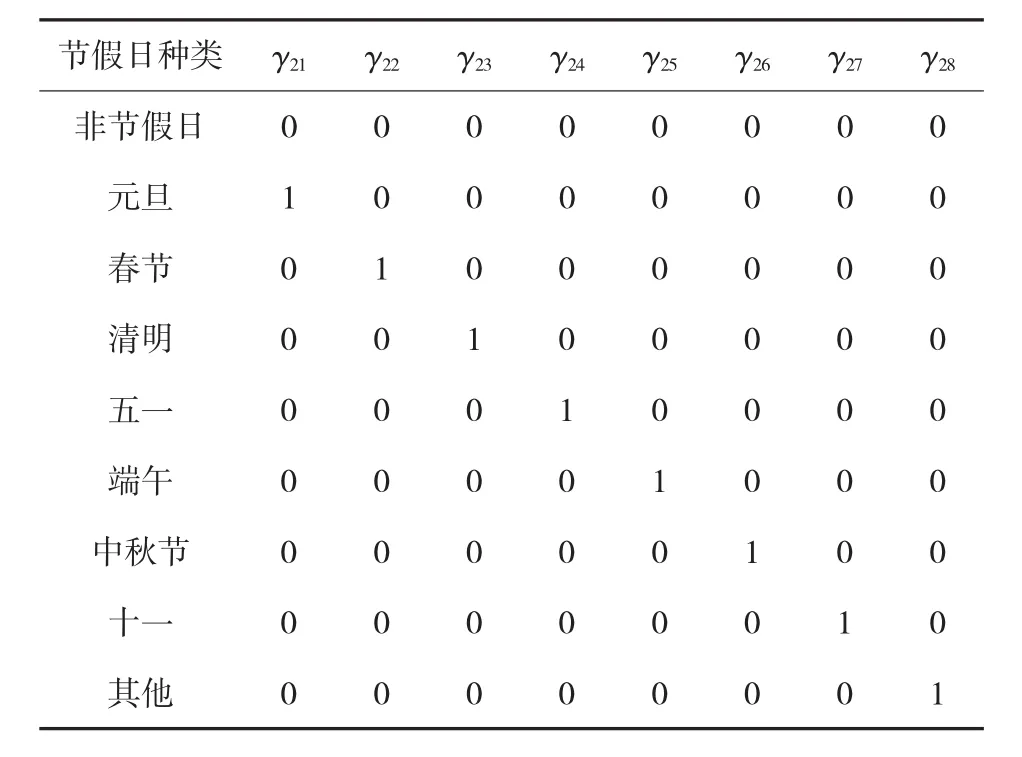
表2 节假日变量赋值

所以修正后的轨道交通常乘客比例数据y的组合预测模型为式（7）：

2.2.2预测

利用式（7）预测2016年3月28日至4月4日（4月2日至4月4日为清明节假期）的日常乘客比例，结果见表3。

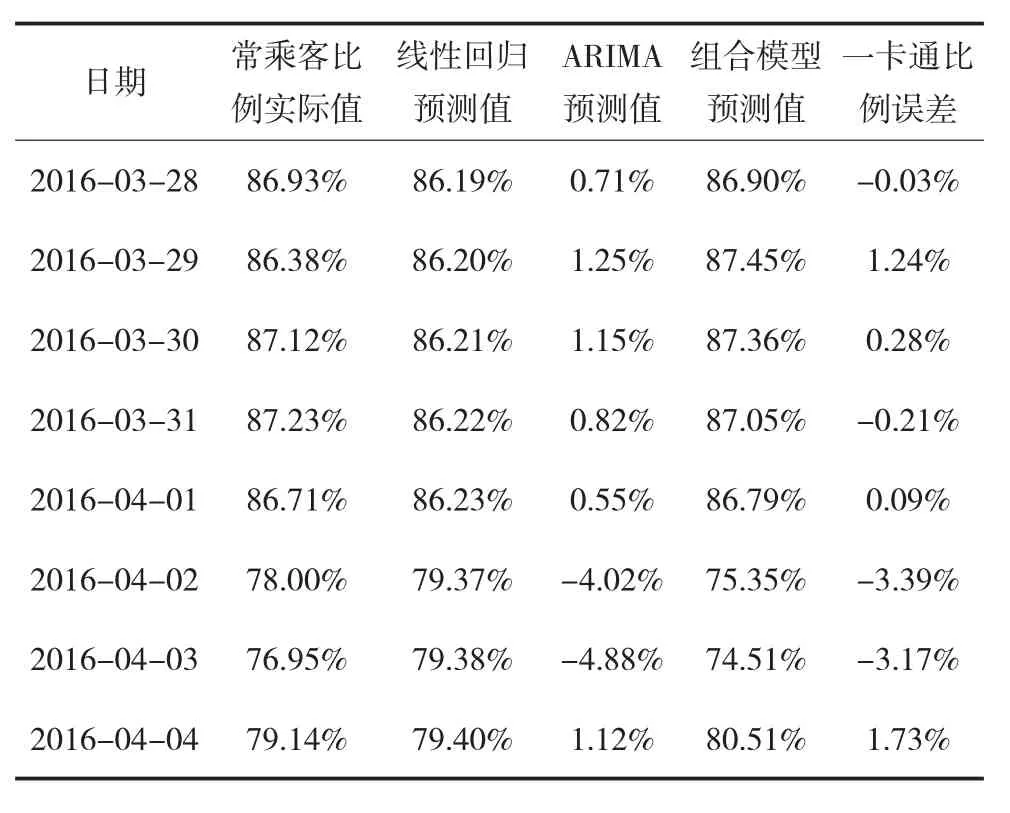
表3 方法二预测结果及误差

2.2.3对比分析

对比表2和表3两种方法的误差，表2（方法一）的平均误差为2.68%，表3（方法二）的平均误差为1.26%，可见方法二的精度高于方法一，并且在节假日（4月2日至4月4日为清明节假期）的预测上，精度明显高于方法一。所以本文构建的基于虚拟变量线性回归和季节ARIMA的组合预测模型（式7），达到了对原有的季节ARIMA的修正效果。

3 结 论

本文依据2015年3月2日至2016年3月27日常乘客比例数据分别建立了常乘客比例ARIMA季节模型以及基于虚拟变量线性回归和季节ARIMA的组合预测模型，对比了两种方法的预测精度，得出以下结论：

（1）基于虚拟变量线性回归和季节ARIMA的组合预测模型的精度高于原有的季节ARIMA的预测模型；

（2）常乘客比例数据具有缓慢递增的趋势和周期为7天的季节性趋势，且递增趋势明显弱于季节性趋势；

（3）节假日的长短对轨道交通日常乘客比例数据有明显的影响，长度为7天的节假日常乘客比例值平均比长度为3天的节假日常乘客比例值低0.069左右；

（4）模型的参数并不是越多越好，在满足残差序列具有较高的白噪声检验的相伴概率（p-Q）情况下，可进行多个模型的比较，综合考虑Adjusted R2、AIC、SC等检验方法，选择最优模型。

基于本文建立的组合预测模型，可以预测近期城市轨道交通路网常乘客比例，掌握常客随时间变化的趋势，为轨道交通运营管理部门提前做好运营组织、运营计划提供量化的参考依据。

[1]鲁放，韩宝明，蔡晓春.城市轨道交通常乘客行为研究[J].城市轨道交通研究，2012（2）：39-42.

[2]G.E.P.Box，G.M.Jenkins，G.C.Reinsel.时间序列分析：预测与控制[M].北京：中国统计出版社，1999．

[3]安鸿志，陈兆国，杜金观，等.时间序列的分析与应用[M]．北京:科学出版社，1983.

[4]杨叔子，吴雅，轩建平，等．时间序列分析的工程应用[M]．武汉：华中科技大学出版社，2007．

[5]孙彩云，杨晓静.乘积ARIMA模型的建立与应用[J].华北科技学院学报，2008，5(2)：85-89.

[6]李勇，吴宝亮，杨秀苔，等.基于乘积ARIMA模型的产品不确定性需求预测[J].系统工程与电子技术，2005，27(1)：60-62.

[7]汤岩，王福林，王吉权.基于季节ARIMA模型的电力系统负荷短期预测[J].数学的实践与认识，2012，42(10)：74-80.

[8]童明荣，薛恒新，林琳.基于季节ARIMA模型的公路交通量预测[J].公路交通科技，2008，25(1)：124-128.

[9]蔡昌俊，姚恩建，王梅英，等.基于乘积ARIMA模型的城市轨道交通进出站客流量预测 [J].北京交通大学学报，2014，38(2)：135-140.

[10]何九冉.城市轨道交通客流统计特征分析及组合预测方法实证研究[D].北京：北京交通大学，2013.

[11]李春晓，李海鹰，蒋熙，等.基于广义动态模糊神经网络的短时车站进站客流量预测[J].都市快轨交通，2015，28(4)：57-61.

[12]王玉萍,陈宽民,杨富社，等.城市轨道交通客流预测结果的技术分析体系 [J].长安大学学报：自然科学版，2011，31(3)：72-79.

[13]郝勇.上海地铁周客流量的数值分析与预测 [J].上海工程技术大学学报，2010，24(1)：60-65.

[14]徐瑞华，徐永实.城市轨道交通线路客流分布的实时预测方法[J].同济大学学报：自然科学版，2011，39(6)：857-861.

U121

A

1009-7716（2017）01-0129-04

10.16799/j.cnki.csdqyfh.2017.01.038

2016-10-31

鲍枫（1976-），女，河南安阳人，副研究员，从事交通信息化研究.