南方稻麦轮作系统下小麦根系的三维分形特征

陈信信，丁启朔，李毅念，薛金林，何瑞银

（1南京农业大学工学院，南京210031；2南京农业大学江苏省智能化农业装备重点实验室，南京210031）

南方稻麦轮作系统下小麦根系的三维分形特征

陈信信1,2，丁启朔1,2，李毅念1,2，薛金林1，何瑞银1,2

（1南京农业大学工学院，南京210031；2南京农业大学江苏省智能化农业装备重点实验室，南京210031）

【目的】根构型直接影响作物的水肥吸收，而定量根构型的相关指标多局限于二维分析，缺乏有效的3D分析指标。论文探讨计算分析根构型3D特征的指标与操作方法，用于定量稻麦轮作制不同耕作方式对小麦根构型的影响。【方法】使用自制的根构型数字化仪，测取田间小麦根系的真实空间拓扑数据，获得根系构型的空间坐标。然后运用Matlab编程实现小麦根构型拓扑数据的虚拟重构，令虚拟根系再现实体根系的空间拓扑。结合分形理论与软件的计算分析功能对虚拟根构型进行分形维计算，分别获取3D分形维数、3D分形丰度、2D分形维数、2D平面分形丰度和单株总根长5个特征指标，以此表达小麦根构型在不同年度、不同耕作方式处理下的时空动态。同时建立不同年度及耕作处理下单株总根长动态与根构型3D分形维数、3D分形丰度、2D分形维数、2D平面分形丰度间的相关关系。【结果】研究发现随着作物生长期的变化，不同年份及不同耕作处理下的小麦根构型指标都表现出稳定增长的趋势。不同之处在于2010—2011年度的小麦根构型指标平稳增长，而2011—2012年度的根系生长速率变化较为剧烈。对比两个年度间的小麦根构型指标发现，免耕和旋耕两种耕作方式对小麦根构型的影响效果相反，在2010—2011年度，旋耕处理方式下的根系指标优于免耕处理方式，而在2011—2012年度，免耕处理方式下的根构型指标表现更优。对于作物生长前期（0—98 d）而言，年度变化引起的根构型指标差异显著大于耕作处理引起的差异，在作物生长后期（98—112 d），年度变化和耕作处理方式对小麦根构型指标的影响较为相近。对比小麦根构型的3D分形维指标和平面分形维指标发现，3D分形维明显区别于平面分形维，这表明根系的三维分形是根构型的必要分析指标。在不同的年度与耕作措施下，单株小麦的总根长与3D分形维数、3D分形丰度、2D分形维数、2D分形丰度都满足指数模型，且显著相关，说明年度因素和耕作措施仅是影响模型的常量参数项。【结论】由计算机软硬件结合分形理论构建的田间小麦根构型的可视化和定量化分析手段是实现小麦根构型精确分析的保证，该分析过程真实再现了田间小麦根构型的时空动态。3D分形指标可以准确定量作物根构型真实的时空动态，在进行根系生长策略的选择及根土关系优化时需要考虑到田间作物根系的实际生长条件和耕作制度。

稻茬麦根系；根构型可视化；3D分形维；平面分形维；根长动态

0 引言

【研究意义】稻麦轮作是中国南方的主导种植制度之一，仅江苏省的种植面积占比就高达 40%[1]。然而年度的水旱交替过程为土壤及作物的管理带来难于协调的矛盾，水旱轮作田土壤结构恶化、作物群体质量差、土地产出低下等现状较为普遍[2-3]。近年的研究表明对作物根构型的调控能够促进水肥吸收[4-5]、令作物适应不良土壤环境[6]、缓解作物根系胁迫[7]，从而保障作物生长与产量[8]。因此定量作物根系的构型特征对改进灌溉与施肥措施、提高作物的水肥利用效率具有重要意义[9]。【前人研究进展】自TATSUMI等[10]首次论证作物根系具有分形特征之后，根系分形已成为作物根系分析的基础方法。EGHBALL等[4]指出可以使用分形维定量根系生长的复杂性；王义琴等[11]使用盒维数计算植物根系的分形特征；杨培岭等[12]给出了表征根系分形特征的数学模型，并用模型分析冬小麦根系的分形特征；杨小林等[13]运用全根挖掘法测量了塔克拉玛干沙漠腹地几种植物根系的分形特征。不过，这些报道都限于平面根构型的分析，并没有涉及作物根系的3D构型。相关的研究表明基于根系二维图像的分形维数值会远小于根系的实际 3D分形维[14]，因此平面根系的分形分析无法反映根系的空间分布特征[15]，然而至今尚无直接定量植物根系3D构型的综合指标[16-17]。【本研究切入点】用于定量根系特征的指标非常多，包括总根长、根表面积、平均直径、分支数量、扎根深度、根生长速率、根系深度分布、根茎比等[18-20]。虽然这些指标涉及根系多方面特征，但是根系在土体空间中的拓扑及3D构型信息仍然缺乏。而恰恰是根系3D构型决定着作物根系的土体空间利用效率及水肥吸收潜力。NIELSEN等[15]使用模拟方法获得虚拟大豆根系并用此研究根系在 1D、2D及3D空间的分形维特征，以此试图建立各维度空间的分形维关系。然而，使用模拟获得的作物根系各维度空间的分形维关系是否符合田间实际仍然没有得到证明。【拟解决的关键问题】本研究围绕田间真实作物根系的3D构型分形分析，定量研究稻茬麦根系的3D构型分形维指标，运用根构型数字化仪[21]并结合Matlab编程软件[22]实现实测根构型的可视化，运用分形理论[23]将田间稻茬麦根构型进行不同尺度的分割，计算根构型的3D拓扑指标——3D分形维，以此描述不同年度不同耕作方式下稻茬麦根构型的时空动态，探究耕作年度和耕作方式对作物根构型的影响。

1 材料与方法

1.1 试验区概况

田间试验于南京农业大学江浦农场进行，试验地为黄棕壤质，多年稻麦轮作发育而成的水稻土，土壤胶结严重，黏闭性强，耕层浅薄，稻季后秋燥条件下表土失水较快，稻茬田免耕播种后小麦成苗难。土壤有机质8.24 g·kg-1，全氮0.97 g·kg-1，速效氮12 mg·kg-1，速效磷12.67 mg·kg-1，速效钾11.05 mg·kg-1，pH 7.6，土壤干密度1.26 g·cm-3，土壤湿密度1.62 g·cm-3，播种前土壤含水量29.28%。

1.2 试验设计

小麦供试品种宁麦13，分别于2010年11月15和2011年11月30播种，设免耕、旋耕2个处理，前茬水稻，每处理 3次重复，随机区组排列，每小区面积10 m2（2 m×5 m）。免耕播种前清除地表残留秸秆[2]，旋耕即常规耕作，均采用精密播种，株行等间距50 mm[21]，种植密度为400粒/m2。取田头碎土盖籽，播前施磷酸二铵375 kg·hm-2，尿素90 kg·hm-2，氯化钾375 kg·hm-2，播后使用农膜覆盖小区，农膜四边压封保墒，成苗后清除农膜，小麦田间管理同大田，3月中旬追肥，自然雨养，不设灌溉。对于小麦的整个生长期而言，该地区的降雨及平均温度如表1所示。自小麦播种日起，每隔14 d取样一次，取样时选择地上部长势均匀的小麦，将直径 160 mm、高200 mm的取样筒置于所取植株对中位置，然后用手锤均匀用力地将样桶打入土层，依次将包含土壤和植株根系的样筒取出带回实验室，每组处理取6株小麦。

1.3 根系3D构型分形计算方法

基于Matlab环境的根系2D构型分形分析是使用盒维数[23]原理的虚拟计算方法。根据陈信信等[21]，韩秋萍等[24]提供的作物根系 2D构型数字化及造型方法，首先进行小麦根系3D构型的数字化，获取根系的绝对空间坐标，以.txt文件保存，利用Matlab编程并使用spline样条插值进行小麦根构型的3D重构（图1），进行后续计算。鉴于根系3D构型数据的获取是通过逐层清除土壤并测试根系在各层土壤的空间坐标，因此在Matlab中重构的小麦虚拟根系仍然保留田间真实根系的空间拓扑（即3D构型）。分别将虚拟根构型向俯视面、正视面和左视面3个投影面上投影并计算3个投影的分形维数和分形丰度[15]。图2显示了根系3D构型对应3个方向上的非扰动2D根构型，该虚拟3D根构型的2D化投影完全有别于洗根法，避免了传统洗根法对原状根构型的破坏[25]。依照本方法得到的2D根构型保留了3D根构型的特定信息，保证2D投影携带3D根构型的特征[26]。

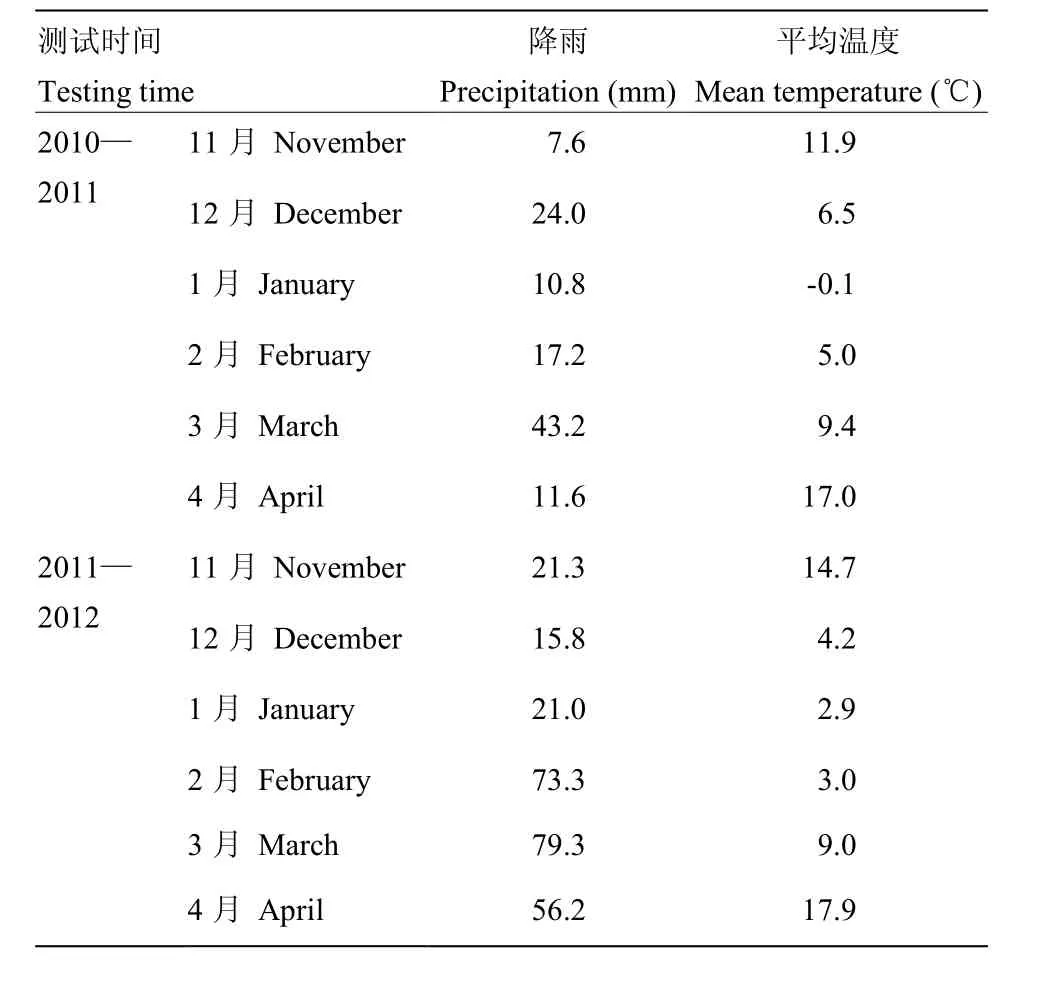
表1 试验地小麦生长期的降雨及平均气温状况Table 1 Precipitation and mean temperature of wheat growing period

根构型的三维分形分析也是基于盒维数原理开发，以半径为ε的D0维球去包覆分形体，当ε→0时，确定包覆所需的最小个N(ε),再由式（1）计算分维数，即盒维数[23]。将重构的根构型（图3-a）进行体覆盖，然后以不同尺度r将正方体分割（图3-b、c），计算出3D分形维。

在 Matlab中计算时，首先设置网格位置坐标[xn-1,yn-1,zn-1]，[xn-1,yn-1,zn]，[xn-1,yn, zn-1]，[xn, yn-1, zn-1]，[xn, yn-1, zn-1]，[xn, yn-1,zn]，[xn, yn, zn-1]，[xn, yn, zn]，当已知点（x0, y0, z0）满足条件：xn-1≤x0＜xn，yn-1≤y0＜yn，zn-1≤z0＜zn，网格就计数一次。然后以根原点为起点，以不同r为网格尺度，计算根系所占的网格数，分别获得r为5、10、20、40和80 mm的网格数N(r)，以log10(N(r))为纵坐标，log10(r)为横坐标，做线性回归（式2），直线的斜率F即根系的3D分形维数，截距log10(K)即根系的3D分形丰度[11]。

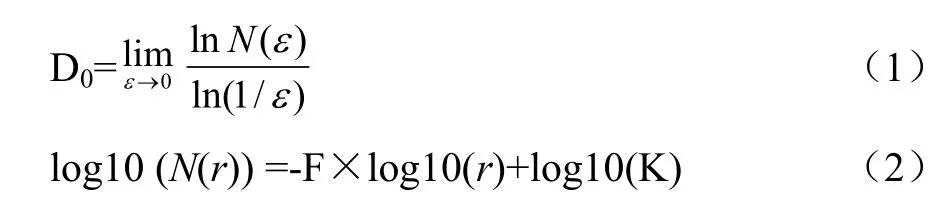
1.4 根构型指标的测定

按照上述方法分别测定2D根构型和3D根构型的分形维和分形丰度等指标。分别计算出从各处理中所取3株植株根系的3向投影2D根构型指标并取均值，对比不同年度、不同耕作方式下根构型的平面投影分形维[26]，展示小麦根构型的平面分形维数和分形丰度动态；分别计算各处理的小麦3D根构型的3D分形维数值及分形丰度，获得不同时期小麦根构型的3D分形维数和分形丰度动态；根据Matlab直接计算每个时期所有小麦根系样品的单株总根长并取均值，以此表达各时期的根长动态。

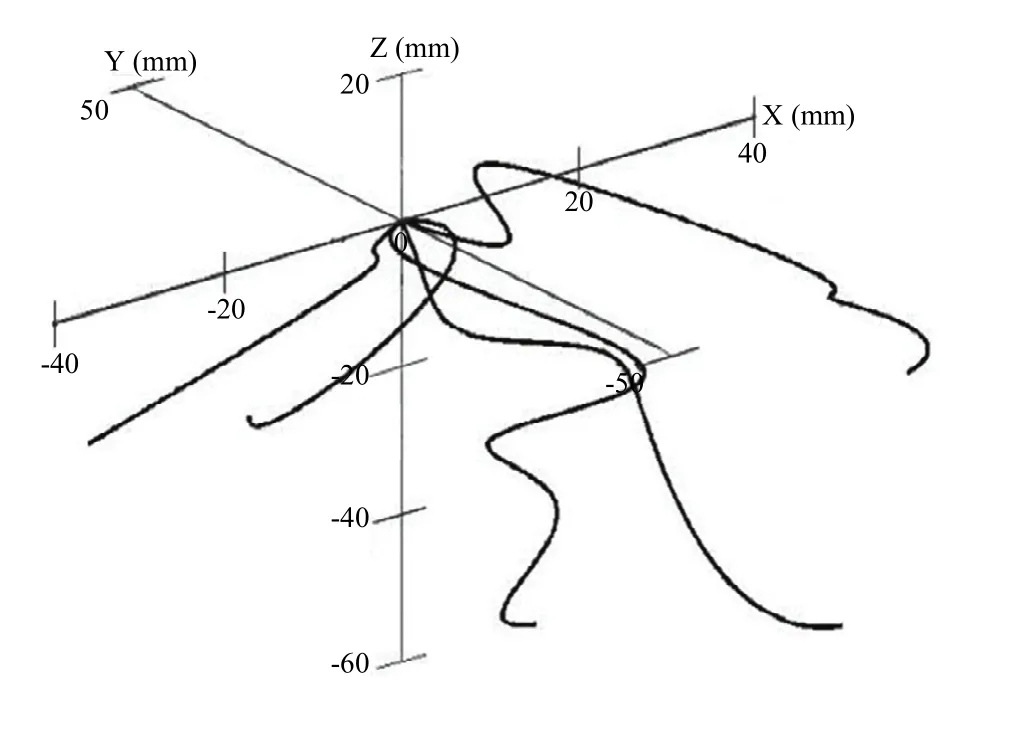
图1 单株小麦根系3D重构及空间坐标状态Fig. 1 3D presentation of wheat root system architecture

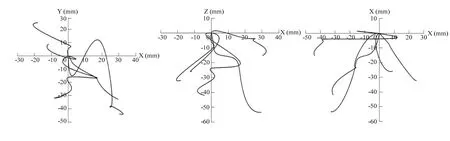
图2 典型小麦根构型的三向投影Fig. 2 2D projections of the wheat root system architecture in three directions

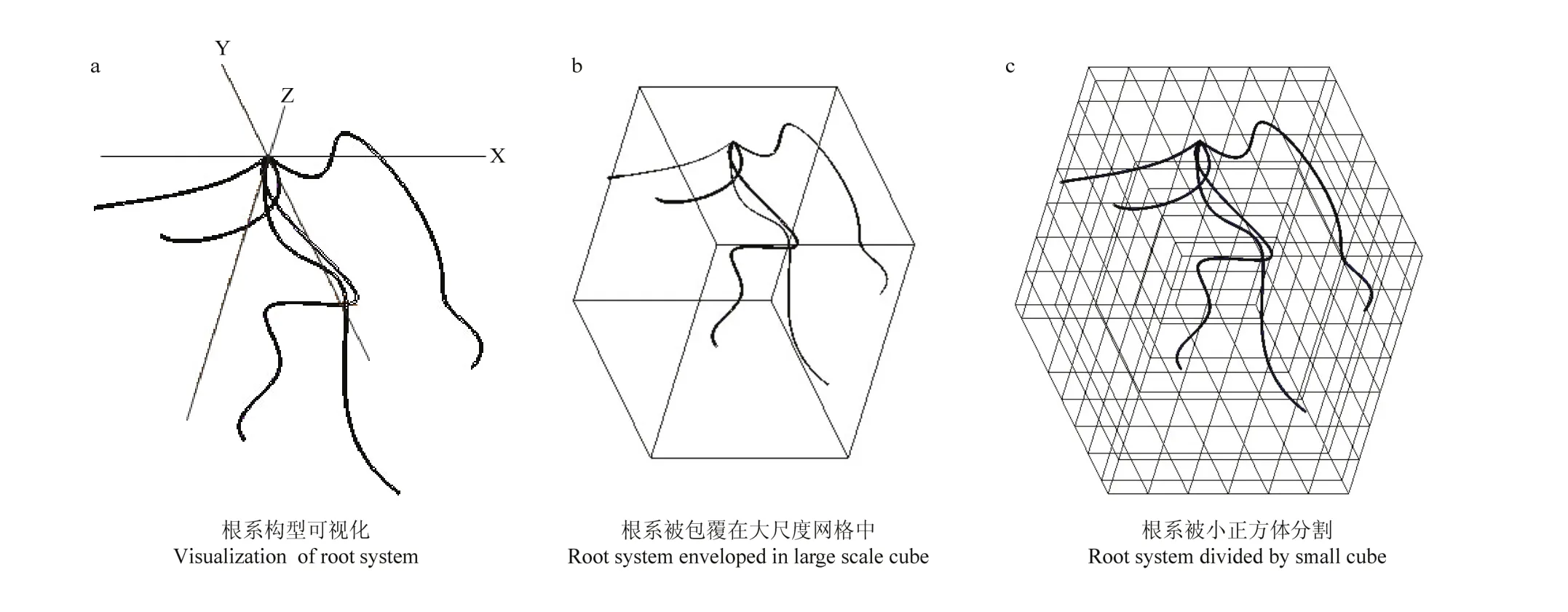
图3 根系可视化及3D分割图Fig. 3 Root architecture visulization and 3D section

1.5 程序框图

基于3D根构型的分形分析计算流程如图4所示，该流程在Matlab中编程实现。

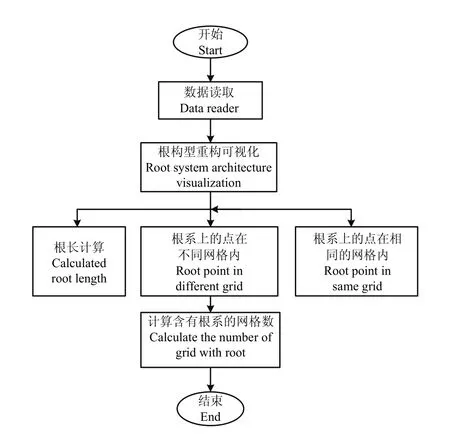
图4 根系分形分析计算的程序框图Fig. 4 Flow chart of the program for calculation of fractal analysis of root system

2 结果

2.1 不同年度、不同耕作方式下稻茬麦根构型的平面

投影分形维动态

图5表明稻茬麦根构型的平面投影分形维数和分形丰度随着取样时间的增长而增加。分形维数反映根系在土壤中的分支状况，能够精确地表征植物根系发育的差异性，而分形丰度主要反映根系在土壤中的拓展体积，可用于描述根系空间占有能力与吸收营养物质的效率[13,27]。根构型的分形动态表明随着时间的增加，根系分支越多，占据土壤空间的能力越强，对根系生长乃至作物的生长发育越有利。研究发现，同一年度下耕作方式显著影响根系生长，但存在年度差异，2010—2011年度旋耕处理的根系分形维数和分形丰度略高于免耕处理，而在2011—2012年度，免耕处理的根系分形维数和分形丰度略高于旋耕处理，表明耕作方式对根系生长的影响是随年度发生变化。

不同年度间小麦根系的生长速率表现出显著的差异性，2010—2011年度的小麦根系分形维数和分形丰度增长趋势较为平缓，而2011—2012年度小麦根系的分形指标增长剧烈。此外，年度对小麦根系生长的影响主要体现在作物生长前期（0—98 d）差异较大，在生长后期（98—112 d）差异逐渐缩小。

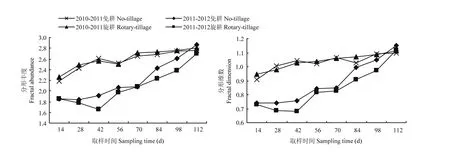
图5 不同年度不同耕作方式下根系投影分形维数动态Fig. 5 Dynamics of 2D fractal dimension of wheat RSA in different years and under different tillage treatments

2.2 不同年度、不同耕作制度下稻茬麦根构型的 3D分形维动态

不同耕作处理的小麦根系分形维数和分形丰度变化趋势是较为一致，而不同年度间的分形维数、分形丰度差异较显著（图6）。图6表明随着生育期的延长，根系3D分形维数和3D分形丰度逐步增大，与2D分形指标的变化趋势相同。2010—2011年度旋耕处理的小麦根系3D分形丰度略优于免耕处理，而免耕处理的小麦根系3D分形维数略优于旋耕处理。2011—2012年度免耕处理的小麦根系3D分形丰度和分形维数都优于旋耕种植方式，表明年度间及耕作方式对小麦根系的差异性影响尚需要进一步研究。

尽管耕作方式能够在一定程度上影响根系发育，但是其差异并不显著，相反，不同年度对于根系的前期生长（0—98 d）影响显著（P＜0.01）。对比同一年度、同一耕作处理的稻茬麦根构型的 2D分形维与3D分形维发现二者间存在显著差异（P＜0.01），这表明作物根系的 2D分形维并不能取代3D分形维分析，3D分形指标是表达作物根构型的必要指标。

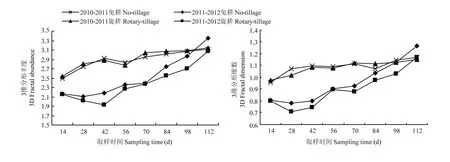
图6 不同年度不同耕作方式下根系3D分形维动态Fig. 6 3D fractal dynamics of wheat RSA in different year and under different tillage treatments

2.3 不同年度、不同耕作方式下稻茬麦根系总长变化动态及其与分形维之间的关系

总根长动态（图 7）显示田间小麦根系的生长在一定时间内处于平稳增加状态，之后根系快速增多。陈信信等[21]的研究也表明根系虽在越冬期会维持一定的根总量，但会发生显著的新老根动态交替过程。本研究在建立分形维与根长指标的关联时发现，根长与根系分形维之间满足指数函数关系（表2）。根长与分形维之间满足关系式：

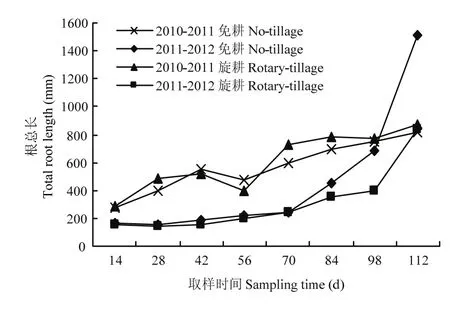
图7 不同年度不同耕作方式下总根长的动态变化图Fig. 7 Dynamics of root length in different years and under different tillage treatments

L=a×eb×FA(FD)或L=a×eb×fa(fd)式中，L表示根系总长，FA、FD（或fa，fd）分别表示三维（或二维）分形丰度和分形维数。

数据表明模型参数a和b不仅与年度有关，也受耕作方式影响。表2显示无论是2D分形维还是3D分形维，其与总根长间的相关性都很高，并且相关系数受到年度影响较大。2010—2011年度免耕处理的总根长受分形维数的影响大于旋耕处理，而总根长受分形丰度的影响要小于旋耕处理，总根长与分形丰度之间的相关系数明显大于其与分形维数之间的相关系数。2011—2012年度则不具有类似的规律。

3 讨论

优化根构型对提高水肥吸收具有重要的意义[4-5]，前人研究多使用小麦根构型的宏观指标来进行描述，如根长密度、根系质量密度及根长密度垂直分布等[21]，然而，此类指标并不能提供小麦根系的3D构型信息。鉴于根构型获取方法和相关指标的缺乏，至今仍没有适合根系 3D构型定量的方法[16-17]。本研究基于根构型数字化仪获取根系的空间分布数据，结合分形理论与Matlab编程，计算根系的平面投影分形维以及根构型的3D分形维，分析了不同年度及不同耕作方式下稻茬麦根系的3维分形特征。

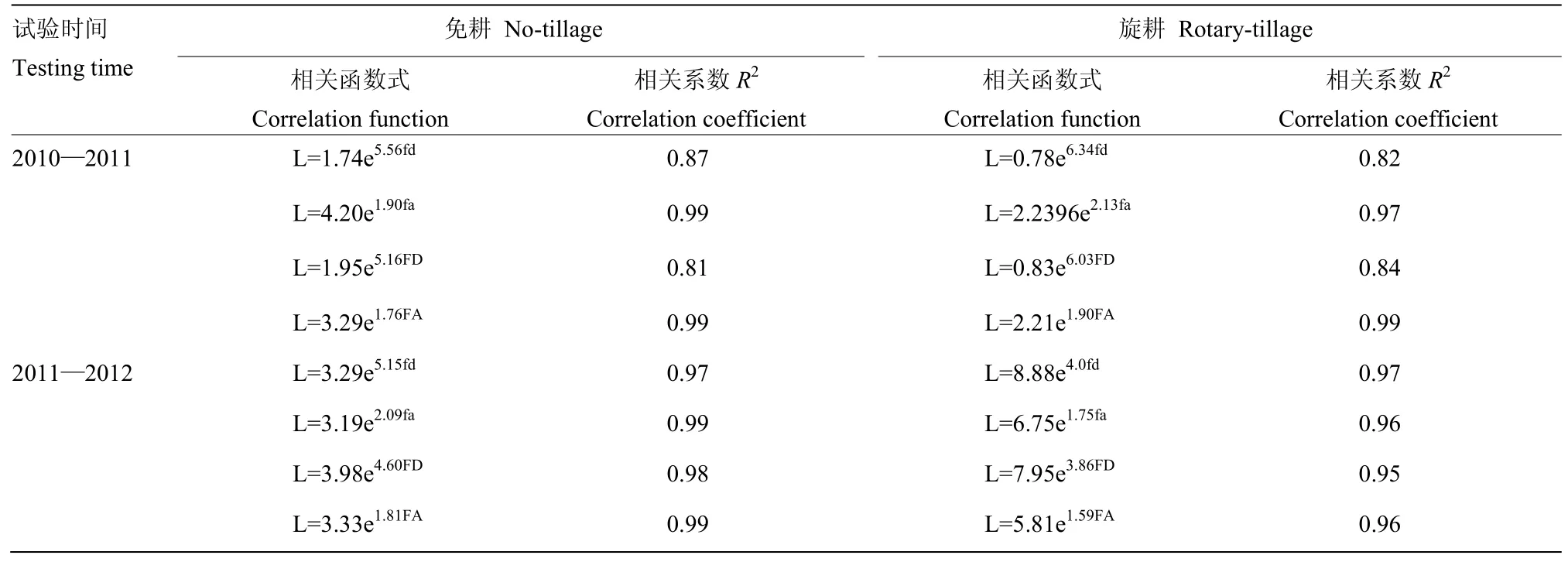
表2 不同年度不同耕作方式下单株根总长与分形维之间的关系Table 2 Correlations between root length and fractal dimensions in different year and under different tillage treatments

根系的分形维直接反映了根系在土体空间中的发育程度以及占据土体空间的能力[27]，同时也在一定程度上反映了植物根系利用土壤水肥的能力[28]。植物根系的分形维数高，根系的发育程度较好，根系分支增多[27]。随着时间的增长，根系的分形维在逐渐增加（图5、图6），表明作物根系占取土体空间和吸收水肥的能力也逐渐增强，这与以往的研究结论一致[10,15]。本文发现年度对于根系的影响较之耕作方式更大，这可能是年度间播期差异所致，前后2个年度的播期相差15 d。张焕军等[29]研究指出播期决定了麦苗生长的起始时间，影响着冬前根苗的生长状况。另外，年度间不同的降雨量也可能影响到根系生长，相比于2010—2011年度，2011—2012年度小麦生长期的降雨量较多，李金才等[30]的研究指出南方地区，小麦生长期降雨过多会造成土壤渍水，使得根层严重缺氧，根系生长发育受阻，根系活力下降，吸收能力下降，引起根系腐烂。

本研究发现2D分形维总小于3D分形维，SILVA等[14]通过研究树木冠层的分形特征指出2D分形维与3D分形维存在本质区别，同时指出使用3D分形维指标和相应方法分析具有分形结构的植株非常必要。BERNTSON等[31]指出植物根系的本质属性是其空间结构性，因此需要相应的指标描述其空间分布特征。所以针对性提出相应的指标对植物根系空间分布进行3D分形分析显得至关重要[27]。

根长是评估根系功能及土壤对其影响的一个重要参数[32]，ARREDONDO等[33]指出根长可以在一定程度上用于表征根系对土壤的探索效率。研究发现，随着生育进程推进，根长在经过一个动态交替过程后会加快增长速度（图7），这也说明2010—2011年度根系生长发展较好，更能有效占据土体空间资源。后期根长的突增可能与三月中旬的追肥相关，也有可能与此时气温的增高有关，刘炜等[34]指出在一定范围内，温度的升高能使根系的生长加快，并促进根系对水肥的吸收并进一步促进根系生长。闫秋艳等[35]也指出，土温会通过影响作物根系对水肥的吸收进而影响作物的生长。丁红等[36]研究指出水肥对于植物根系的生长具有诱发作用。

从根系的各个生长指标可以看出，对于不同年度而言，2种耕作方式下根系的生长动态相反（图5—7），这要求对应不同的自然环境，宜选择不同的耕作方式。在降雨量适中的条件，旋耕相对于免耕而言，耕层土壤透水透气性更好，但在降雨过多时旋耕模式造成的150 mm以下土层的压实及犁底层的形成[37]，不利于水分流通，导致根际渍水，从而对根系生长不利。KUKAL等[38]指出稻麦轮作过程中稻季土壤淹水打浆及麦季旋耕作业而形成的犁底层会严重限制土壤中水肥的流动。根系生长及构型分布是耕作方式[39]、水肥处理[30,36]、土壤状况[40]、作物品种[27]等多重因素综合作用的结果，所以确切的结论则需要更加详细、针对性更强的试验加以论证。

已有研究表明根系分形维数与根总长显著正相关[41]，SMITH等[42]指出根系分形特征与根系长度之间具有显著关系。本研究基于田间试验建立稻茬麦根系的分形维数、根系分形丰度与根总长之间的关系式，发现其满足指数关系式，与前人的发现较为一致。杨培岭等[12]研究指出，植物根长与根系分形维数之间存在一定的关系，随着根长的增加或者减少，根系的分形维数也在增加或者减少。本研究表明不同耕作方式及年限的根系分形维及根长变化不同，年度间的差异性显著大于耕作方式，因此年度间的气候特征不同所起的影响更为显著。WHITE等[40]发现，作物在不同的生长环境中根系的生长发育差异显著。生长介质的不均匀性决定了根系在土体空间中的各向异性，这也进一步表明仅对田间作物根系实施平面分形分析是远远不够的[11-12]。本研究首次综合使用分形理论与田间根系数字化方法[21]实现了田间稻茬麦根构型的三维分形分析，得出的根系平面投影分形维与三维分形维之间的显著差异也表明对植物根系进行三维分形维分析的必要性。

4 结论

基于田间作物根构型数字化仪和编程语言实现的根构型可视化能够直观展示田间作物根系真实的分布状态，结合分形理论进一步计算根系的平面分形维和3D分形维，并以此为指标对稻茬麦根构型特征进行定量化描述，这一技术路线准确可靠，实用性强。

针对南方稻茬麦根构型分布开展连续2年跟踪测试，得到不同年度、不同耕作方式下的小麦根构型特征，发现3D分形维数值要大于平面分形维数值，且二者之间存在显著性差异（P＜0.01）；耕作方式对根构型的影响要明显小于生长年度对构型的影响；然而无论是3D分形维还是平面投影分形维，其与单株根系总长之间总满足指数关系式。

直接定量田间作物根构型指标的提出有利于获取根系实际的空间拓扑信息，这对于指导调控田间作物管理、改善根系生长环境、优化根系分布提高作物产量具有重要的意义，然而本研究的不足之处是没有进行大量的样本分析，这有待后续进一步研究。

[1] 常志州, 王德建, 杨四军, 王灿, 张斯梅. 对稻麦秸秆还田问题的思考. 江苏农业学报, 2014, 30(2): 304-309.

CHANG Z Z, WANG D J, YANG S J, WANG C, ZHANG S M. Thoughts on returning straw to field. Jiangsu Journal of Agricultural Science, 2014, 30(2): 304-309. (in Chinese)

[2] 李朝苏, 汤永禄, 吴春, 黄钢. 播种方式对稻茬小麦生长发育及产量建成的影响. 农业工程学报, 2012, 28(18): 36-43.

LI C S, TANG Y L, WU C, HUANG G. Effect of sowing patterns on growth, development and yield formation of wheat in rice stubble land. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(18): 36-43. (in Chinese)

[3] 汤永禄, 程少兰, 李朝苏, 钟贵祥. 稻茬麦半旋高效播种技术. 四川农业科技, 2010(9): 20-21.

TANG Y L, CHENG S L, LI C S, ZHONG G X. High efficiency seeding technique of half-tillage in wheat after rice. Science and Technology of Sichuan Agriculture, 2010(9): 20-21. (in Chinese)

[4] EGHBALL B, SETTIMI J R, MARANVILLE J W, PARKHURST A M. Fractal analysis for morphological description of corn roots under nitrogen stress. Agronomy Journal, 1993, 85(2): 287-289.

[5] FITTER A H, STICKLAND T R. Fractal characterization of root-system architecture. Functional Ecology, 1992, 6(6): 632-635.

[6] ROBINSON D. The responses of plants to non-uniform supplies of nutrients. New Phytologist, 1994, 127(4): 635-674.

[7] ACUNA T L B, WADE L J. Genotype × environment interactions for root depth of wheat. Field Crops Research, 2012, 137(9): 2877-2888.

[8] AHMADI N, AUDEBERT A, BENNETT M J, BISHOPP A, OLIVEIRA A C, COURTOIS B, DIEDHIOU A, DIEVART A, GANTET P, GHESQUIERE A, GUIDERDONI E, HENRY A, INUKAI Y, KOCHIAN L, LAPLAZE L, LUCAS M, LUU D T, MANNEH B, MO X, MUTHURAJAN R, PERIN C, PRICE A, ROBIN S, SENTENAC H, SINE B, UGA Y, VERY A A, WISSUWA M, WU P, XU J. The roots of future rice harvests. Rice, 2014, 7(1): 1-9.

[9] 曹宏鑫, 石春林, 金之庆. 植物形态结构模拟与可视化研究进展.中国农业科学, 2008, 41(3): 669-677.

CAO H X, SHI C L, JIN Z Q. Advances in researches on plant morphological structure simulation and visualization. Scientia Agricultura Sinica, 2008, 41(3): 669-677. (in Chinese)

[10] TATSUMI J, YAMAUCHI A, KONO Y. Fractal analysis of plants root systems. Annals of Botany, 1989, 64(5): 499-503.

[11] 王义琴, 张慧娟, 杨奠安, 白克智, 匡廷云. 大气CO2浓度倍增对植物幼苗根系生长影响的分形分析. 科学通报, 1998, 16(43): 1736-1738.

WANG Y Q, ZHANG H J, YANG D A, BAI K Z, KUANG T Y. Fractal analysis of the effects from CO2concentration doubling in atmosphere to root growth of seedlings. Chinese Science Bulletin, 1998, 16(43):1736-1738. (in Chinese)

[12] 杨培岭, 罗远培. 冬小麦根系形态的分形特征. 科学通报, 1994, 39(20): 1911-1913.

YANG P L, LUO Y P. Fractal characteristics of winter wheat root morphology. Chinese Science Bulletin, 1994, 39(20): 1911-1913. (in Chinese)

[13] 杨小林, 张希明, 李义玲, 解婷婷, 王伟华. 塔克拉玛干沙漠腹地几种植物根系分形特征. 干旱区地理, 2009, 32(2): 249-254.

YANG X L, ZHANG X M, LI Y L, XIE T T, WANG W H. Root fractal characteristics at the hinterland of Taklimakan Desert. Arid Land Geography, 2009, 32(2): 249-254. (in Chinese)

[14] SILVA D D, BOUDON F, GODIN C, PUECH O, SMITH C, SINOQUET H. A critical appraisal of the box counting method to assess the fractal dimension of tree crowns. Lecture Notes in Computer Science, 2006, 4291: 751-760.

[15] NIELSEN K L, JOMATHAN P L, WEISS H N. Fractal geometry of bean root systems: Correlations between spatial and fractal dimension. American Journal Botany, 1997, 84(1): 26-33.

[16] 梁泉, 廖红, 严小龙. 植物根构型的定量分析. 植物学通报, 2007, 24(6): 695-702.

LIANG Q, LIAO H, YAN X L. Quantitative analysis of plant root architecture. Chinese Bulletin of Botany, 2007, 24(6): 695-702. (in Chinese).

[17] 朱同林, 方素琴, 李志垣, 刘玉涛, 廖红, 严小龙. 基于图像重建的根系三维构型定量分析及其在大豆磷吸收研究中的应用. 科学通报, 2006, 51(16): 1885-1893.

ZHU T L, FANG S Q, LI Z H, LIU Y T, LIAO H, YAN X L. 3D quantitative analysis of root system architecture base on image reconstruction and its application to crop phosphorus research. Chinese Science Bulletin, 2006, 51(16): 1885-1893. (in Chinese)

[18] REUBENS B, POESEN J, DANJON F, GEUDENS G, MUYS B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: A review. Trees, 2007, 21(4): 385-402.

[19] FANG S Q, YAN X L, LIAO H. 3D reconstruction and dynamic modeling of root architecture in situ and its application to crop phosphorus research. Plant Journal, 2009, 60(6): 1096-1108.

[20] IYER-PASCUZZI A S, SYMONOVA O, MILEYKO Y, HAO Y, BELCHER H, HARER J, WEITZ J S, BENFEY P N. Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiology, 2010, 152(3): 1148-1157.

[21] 陈信信, 丁启朔, 丁为民, 田永超, 朱艳, 曹卫星. 基于虚拟植物根系技术的冬小麦根系3D构型测试与分析. 中国农业科学, 2014, 47(8): 1481-1488.

CHEN X X, DING Q S, DING W M, TIAN Y C, ZHU Y, CAO W X. Measurement and analysis of 3D wheat root system architecture with a virtual plant tool kit. Scientia Agricultura Sinica, 2014, 47(8): 1481-1488. (in Chinese)

[22] 张志涌. 精通MATLAB R2011a. 北京: 北京航空航天大学出版社, 2011.

ZHANG Z Y. MATLAB R2011a Application. Beijing: Beijing University of Aeronautics and Astronautics Press, 2011. (in Chinese)

[23] 李火根, 阮锡根, 王友菁, 黄敏仁, 王明庥. 森林复杂性状分维数计算软件（FDC1.0）的研制与应用. 南京林业大学学报(自然科学版), 2004, 28(3): 5-8.

LI H G, RUAN X G, WANG Y J, HUANG M R, WANG M X. Development and application of software for Fractal Dimension Calculation (FDC1.0) of complex traits in forest trees. Journal of Nanjing Forestry University (Natural Sciences Edition), 2004, 28(3): 5-8.(in Chinese)

[24] 韩秋萍, 丁启朔, 潘根兴, 丁为民, 周裕辉. 基于Pro/E的土壤结构与小麦幼苗期根系关系模拟与分析. 中国农业科学, 2010, 43(22): 4598-4604.

HAN Q P, DING Q S, PAN G X, DING W M, ZHOU Y H. Modeling and analyzing the relationship between soil structure and wheat seeding root with Pro/E. Scientia Agricultura Sinica, 2010, 43(22): 4598-4604. (in Chinese)

[25] MAIRHOFER S, PRIDMORE T. RooTrak: Automated recovery of three-dimensional plant root architecture in soil from x-ray microcomputed tomography images using visual tracking. Plant Physiology, 2012, 158(2): 561-569.

[26] 陈信信, 丁启朔, 李毅念, 丁为民, 田永超. 稻茬麦根构型可视化与三向分型维研究. 农业机械学报, 2015, 46(3): 328-335.

CHEN X X, DING Q S, LI Y N, DING W M, TIAN Y C. Study on the visualization of post-paddy wheat rooting system and 3D fractal dimensions. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 328-335. (in Chinese)

[27] 汪洪, 金继运, 山内章. 以盒维数法分形分析水稻根系形态特征及初探其与锌吸收积累的关系. 作物学报, 2008, 34(9): 1637-1643.

WANG H, JIN J Y, SHAN N Z. Fractal analysis of root system architecture by box-counting method and its relationship with Zn accumulation in rice. Acta Agronomica Sinica, 2008, 34(9): 1637-1643. (in Chinese)

[28] WANG H, SIOPONGCO J, WADE L J, YAMAUCHI A. Fractal analysis on root systems of rice plants in response to drought stress. Environmental and Experimental Botany, 2009, 65(3): 338-344.

[29] 张焕军, 郁红艳, 项剑, 丁维新. 播种时间对豫北地区小麦农学指标、生理指标及产量的影响. 中国生态农业学报, 2012, 20(8): 1030-1036.

ZHANG H J, YU H Y, XIANG J, DING W X. Effect of sowing date on agronomic, physiologic and yield indicators of wheat in North Henan province. Chinese Journal of Eco-Agriculture, 2012, 20(8): 1030-1036. (in Chinese)

[30] 李金才, 魏凤珍, 王成雨, 尹钧. 孕穗期土壤渍水逆境对冬小麦根系衰老的影响. 作物学报, 2006, 32(9): 1355-1360.

LI J C, WEI F Z, WANG C Y, YIN J. Effects of waterlogging on senescence of root system at booting stage in winter wheat. Acta Agronmica Sinica, 2006, 32(9): 1355-1360. (in Chinese)

[31] BERNTSON G M. Modelling root architecture: are there tradeoffs between efficiency and potential of resource acquisition? New Phytologist, 1994, 127(3): 483-493.

[32] GAISER T, PERKONS U, KÜPPER P M, KAUTZ T, UTEAUPUSCHMANN D, EWERT F, ENDERS A, KRAUSS G. Modeling biopore effects on root growth and biomass production on soils with pronounced sub-soil clay accumulation. Ecological Modelling, 2013, 256(1759): 6-15.

[33] ARREDONDO J T, JOHNSON D A. Allometry of root branching and its relationship to root morphological and functional traits in three range grasses. Journal of Experimental Botany, 2011, 62(15): 5581-5594.

[34] 刘炜, 杨君林, 许安民, 张建平, 田霄鸿, 高亚军. 不同根区温度对冬小麦生长发育及养分吸收的影响. 干旱地区农业研究, 2010, 28(4): 197-201.

LIU W, YANG J L, XU A M, ZHANG J P, TIAN X H, GAO Y J. Effect of different root zone temperature on growth development and N, P and K uptake of winter wheat. Agricultural Research in the Arid Areas, 2010, 28(4): 197-201. (in Chinese)

[35] 闫秋艳, 段增强, 李汛, 董金龙, 王嫒华, 邢鹏, 董飞. 根区温度对黄瓜生长和土壤养分利用的影响. 土壤学报, 2013, 50(4): 752-760.

YAN Q Y, DUAN Z Q, LI X, DONG J L, WANG A H, XING P, DONG F. Effect of root zone temperature on growth of cucumber and nutrient utilization in soils. Acta Pedologica Sinica, 2013, 50(4): 752-760. (in Chinese)

[36] 丁红, 张智猛, 戴良香, 杨吉顺, 慈敦伟, 秦斐斐, 宋文武, 万书波.水氮互作对花生根系生长及产量的影响. 中国农业科学, 2015, 48(5): 872-881.

DING H, ZHANG Z M, DAI L X, YANG J S, CI D W, QIN F F, SONG W W, WAN S B. Effects of water and nitrogen interaction on peanut root growth and yield. Scientia Agricultura Sinica, 2015, 48(5): 872-881. (in Chinese)

[37] AHMAD N, HASSAN F U, BELFORD R K. Effect of soil compaction in the sub-humid cropping environment in Pakistan on uptake of NPK and grain yield in wheat (Triticum aestivum): I. compaction. Field Crops Research, 2009, 110(1): 54-60.

[38] KUKAL S S, AGGARWAL G C. Puddling depth and intensity effects in rice-wheat system on a sandy loam soil: I. development of subsurface compaction. Soil & Tillage Research, 2003, 72(3): 1-8.

[39] 王永华, 王玉杰, 冯伟, 王晨阳, 胡卫丽, 轩红梅, 郭天财. 两种气候年型下不同栽培模式对冬小麦根系时空分布及产量的影响. 中国农业科学, 2012, 45(14): 2826-2837.

WANG Y H, WANG Y J, FENG W, WANG C Y, HU W L, XUAN H M, GUO T C. Effects of different cultivation patterns on the spatial-temporal distribution characteristics of roots and grain yield of winter wheat in two climatic years. Scientia Agricultura Sinica, 2012, 45(14): 2826-2837. (in Chinese)

[40] WHITE P J, GEORGE T S, GREGORY P J, BENGOUGH A G, HALLETT P D, MCKENZIE B M. Matching roots to their environment. Annals of Botany, 2013, 112(2): 207-222.

[41] 陈吉虎, 余新晓, 有祥亮, 刘苹, 张长达, 谢港. 不同水分条件下银叶椴根系的分形特征. 中国水土保持科学, 2006, 4(2): 71-74.

CHEN J H, YU X X, YOU X L, LIU P, ZHANG C D, XIE G. Fractal characteristics of Tilia tomentosa's root system under different water conditions. Science of Soil and Water Conservation, 2006, 4(2): 71-74. (in Chinese)

[42] SMITH D M. Estimation of tree root lengths using fractal branching rules: A comparison with soil coring for Grevillea robusta. Plant and Soil, 2001, 229(2): 295-304.

（责任编辑 杨鑫浩）

Three Dimensional Fractal Characteristics of Wheat Root System for Rice-Wheat Rotation in Southern China

CHEN XinXin1,2, DING QiShuo1,2, LI YiNian1,2, XUE JinLin1, HE RuiYin1,2
(1College of Engineering, Nanjing Agricultural University, Nanjing 210031;2Key Laboratory of Intelligent Agricultural Equipment in Jiangsu Province, Nanjing Agricultural University, Nanjing 210031)

【Objective】Root system architecture (RSA) has a significant effect on water uptake and nutrient absorption. However, relevant indices for the quantification of crop RSAs are limited to 2D fractal analysis. Analytical tools for 3D fractal analysis on crop RSAs are lacking. Thus there is a need to investigate the related parameters and operational procedures suitable for the analysis of the 3D characteristics of crop RSAs.【Method】A self-fabricated digitizer for crop RSAs was used to measure thetopological parameters of the field-grown wheat root, and the spatial dimensions of wheat RSAs were obtained. Virtual wheat RSAs were then modeled and reconstructed with Matlab programming, which guaranteed a realization of the real-world wheat RSAs with virtual reality. The fractal theory was then introduced into the computing software to calculate the fractal parameters of the modeled virtual wheat RSAs, including 3D fractal dimension, 3D fractal abundance, 2D fractal dimension, 2D fractal abundance and total root length. These parameters were used to quantify the dynamics of wheat RSAs, in both the 2 experimental years and the 2 tillage treatments. Correlations among 3D fractal dimension, 3D fractal abundance, 2D fractal dimension, 2D fractal abundance and total root length were also analyzed.【Result】It was found that all the RSA-related parameters were steadily increased along wheat developmental stages, in either different years or under different tillage treatments. Differences between the 2 years appeared as the 2010-2011 crop season revealed a steady increase of RSA-related parameters, while the 2011-2012 crop season observed a more radical increase of root elongation rate. A comparison between the 2 years revealed that tillage treatment had a contrasting effect from year to year, with a better crop performance under rotary till than no-till in the first year, whereas the no-till treatment in 2011-2012 outperformed the first year. At the early stage (0-98 d), the crop season had pronounced influences on wheat RSAs, as compared with tillage treatments. At the ensuing stage (98-112 d), however, annual difference of wheat RSA parameters was as similar as the tillage treatments. A comparison between 3D fractal parameters with the 2D parameters revealed that 3D parameters were markedly contrasted with the 2D parameters, indicating that introducing the 3D parameters for crop RSA analysis is necessary. Disregard annual difference and tillage treatment, all the dynamics of 3D fractal dimension, 3D fractal abundance, 2D fractal dimension, 2D fractal abundance and total root length satisfied power law functions and were all co-related significantly. This means that the effects of crop season and tillage treatment were only related to the coefficients of the power law models. 【Conclusion】 It was concluded that the visualization and analytical tools developed with hardware and software integration and combined with fractal theory was a guarantee for precise quantification of crop root system architectures. Such an analytical tool allows recasting the spatio-and-temporal dynamics of field crop RSAs with modeled virtual roots. 3D fractal parameters could be used as a precision analytical tool for crop RSAs. In selecting root elongation tactics and optimizing the root-soil interactions an important consideration should be taken to match the crop root with its soil environment and the tillage system.

paddy wheat root system; visualization of root system architecture (RSA); 3D fractal analysis; 2D fractal analysis; root length dynamics

2016-06-13；接受日期：2016-11-01

国家重点研发计划“粮食丰产增效科技创新”重点专项（2016YFD0300900）、江苏省农机基金（201-051028）

联系方式：陈信信，E-mail：lingyinyu@163.com。通信作者丁启朔，E-mail：qsding@njau.edu.cn