刮擦全息透射成像的研究*

薛 瑞 赵 磊 王 涛 程俭中

(成都理工大学应用物理系 四川 成都 610059)

刮擦全息透射成像的研究*

薛 瑞 赵 磊 王 涛 程俭中

(成都理工大学应用物理系 四川 成都 610059)

针对刮擦全息在透射成像方面的缺失，先提出了基于几何光学的理论解释，然后对两面刻有不同划痕的亚克力板进行了一系列成像实验，从而验证了理论的正确性.通过将刮擦全息透射成像与反射成像进行对比，指出了二者在理论和实验上的异同.接着给出了透射成像修正系数的较精确推导，推导过程反映出了板材对透射成像的影响.最后，指出了刮擦全息透射成像的实际利用价值及其对进一步完善刮擦全息技术的重要作用.

刮擦全息 透射成像 反射成像 折射 亚克力板

1 引言

刮擦全息是与基于波动理论的传统全息[1]不同的一种全息实现形式.同后者相比，它对产生全息效果的光源没有苛刻的要求，更易于实现.刮擦全息有两种成像方式，即反射成像和透射成像.

近几十年内有关刮擦全息的研究成果如下：20世纪70年代，Gabriel Liebermann[2]发现光滑平面上的圆弧形划痕可以产生3D效果.这种能产生3D效果的刮擦方式在同世纪90年代由Willian J Beatty[3，4]独立发现，Beatty还指出了刮擦全息与基于波动理论的传统全息[1]之间的联系.2008年，文献[5]依据几何学知识给出了绘制无形变刮擦全息图的方法，解决了图像的形变问题.2015年，文献[6]新提出了一种能产生立体图像的划痕规则，并以反射定律为基础，从理论上解释了刮擦全息的反射成像.文献[7]也对刮擦全息反射成像提供了理论解释，文献[8]则提供了一种用激光雕刻刮擦全息的方法.至此,刮擦全息反射成像的理论以及制作刮擦全息的技术已经臻于完善了.

反射定律与折射定律虽然是实验定律，但在波动光学方面，它们都能由电磁场在两种不同介质面上的边值关系[9]导出；在几何光学方面，都能由费马原理[10]导出.由此看来，这两条定律是同一基本原理在不同情况下的不同表达形式.而刮擦全息的两种成像方式就分别由这两条定律决定.

因此，上述研究者们在对刮擦全息反射成像进行实验和理论推导后，猜想透射成像将遵从相同的规律，便没有进一步研究，从而导致了刮擦全息透射成像在理论及实验上的缺失.

本文先对刮擦全息透射成像进行了理论上的推导及分析，并将其数学模型程序化和可视化.然后通过实验证明了理论的正确性，并对比分析了刮擦全息的透射成像与反射成像.

2 刮擦全息透射成像的数学模型

2.1 模型的建立

以WillianJBeatty[3,4]提出的划痕规则在某一透明光滑平板的上表面刻上划痕，其中某一条划痕的透射成像原理图如图1所示.以板的上表面为 xOy面，以其指向光源一侧的法线方向为z轴正方向，建立空间直角坐标系.来自光源G的一束光射到此划痕上的某一点B处，在上下表面各发生一次折射后，射到观察者F1处(由于板很薄，因此图1略去了光在板下表面的折射).在上述过程中，B点就是F1处的观察者看到的亮点.设圆形划痕的圆心A为

(x0,y0,z0)，半径为R，AB与x轴正方向的夹角为θ.因此，亮点B的坐标为(x0+Rcosθ,y0+Rsinθ,z0).

图1 透射成像的原理图(第三视角)

如图2所示，将划痕凹槽的横截面看作一个半圆，B是它的圆心，O′点是半圆上产生透射亮点的一个面元(简称亮点面元)，在后面的处理中，将B点和O′点看作同一个点.在图2中，n是沿亮点面元法线方向的一个矢量，e是与板的两表面垂直的矢量.板的厚度为d，空气的折射率为n1，板的折射率为n2.

图2 刮擦全息透射成像的原理图(凹槽的截面)

由图2可得

(n-y0-Rsinθ)j+(p-z0)k

(b-y0-Rsinθ)j+(c-z0)k

由上面两式可看出，在观察者、光源和圆弧圆心位置及其半径已知的情况下，能求出θ，从而确定光点B在xOy平面上的位置.由光源发出的光经过两次折射后进入观察者的眼睛，这两次折射分别发生在板的上下表面.下面分别分析这两次折射，以求出θ.

第一次折射：

n1sinθ1=n2sinθ2

(1)

由矢量叉乘的性质可得

(2)

联立式(1)、(2)得

(3)

(4)

将式(4)代入式(3)，消去n得

(5)

将式(5)代入式(4)得

(6)

第二次折射:

(7)

而由图2可知

(8)

式(6)、(7)、(8)联立得

(9)

设

则

(10)

由图2可得

且

因此

(11)

我们要求的是n的方向，而不是n的大小，因此等式两边同时乘以常数k′后等式依然成立.所以

(12)

由绘制划痕的过程可知，整个划痕的凹槽是回转体，因此亮点面元对应法线、沿AB方向的直线与过O′点且平行于z轴的直线在同一平面内.由矢量混合积的相关性质可得

其中

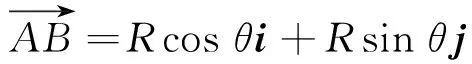
ez=k

代入各矢量的分量可得

nycosθ=nxsinθ

(13)

而由式(12)的分量式可得

(14)

将式(14)代入式(13)可解得

(15)

sinθ与cosθ取相同符号.其中

设

由图2可知，当观察者和光源离板的距离均远大于圆弧半径R时，可以忽略R，即

(16)

因此

(17)

式(15)和式(17)即刮擦全息透射成像理论的最终结论.这个结论可以确定亮点B(O′)在板上表面的位置.

2.2 与反射成像的模型进行对比

文献[7]的刮擦全息反射成像原理图如图3所示.

图3 刮擦全息反射成像的原理图(第三视角)

文献[7]所得的反射成像理论的最终结论为

(18)

其中

(19)

将上述结论和式(15)、(17)进行对比就会发现，刮擦全息透射成像与反射成像的结论几乎完全相同.但在透射成像理论中引入的修正系数不等于反射成像理论中引入的修正系数，前者比后者多了一个k2(k2≪k，精度要求不高时可以忽略不计).本文将在后面进一步分析造成这种不同的原因.

2.3 模型的程序化与可视化

首先选用立体字母 “CDUT”的正等轴测图[11]作为绘制划痕的原图.在平面直角坐标轴上用一系列等间距的点描绘出原图的轮廓，并记录下这些点对应的坐标值，这些点就是圆弧形划痕的圆心.

用Matlab语言将2.1中的理论(不略去k2)编写成函数1，然后将各个系数以及光源、观察者和上面得到的一系列点的坐标输入函数1，运行程序后得到图4(b).以HIT的文献[7]的刮擦全息反射成像理论为基础编写出函数2，然后将光源、观察者和上面得到的一系列点的坐标输入函数2，运行程序得到图4(a).

再以一段直线为原图，重复上述步骤，并将各个系数以及光源、观察者和描绘直线的一系列点的坐标输入函数1，运行程序后得到图4(c).

图4 计算机仿真结果

3 实验与现象

3.1 实验步骤

用Willian J Beatty[5]提出的划痕规则绘制刮擦全息图,需要的材料及工具有立体字母”CDUT”的正等轴测图、若干块黑色亚克力板、分规、签字笔.

以这个正等轴测图为原图在板的正面绘制划痕的步骤如下：

(1)将原图固定在板上,用离散的点描绘出原图的边框.

(2)将分规两脚距离固定为R，然后用分规分别以原图边框上的每个点为圆心，以半径为R画圆弧(此圆弧小于半圆).

用笔在亚克力板的反面画上一段直线，并以这段直线为原图绘制刮擦全息图.这段直线的划痕画法同上述正等轴测图的画法相比，第一步不变，第二步中的圆弧改成一个整圆，同时缩小半径R.最终得到一个两面均有划痕的亚克力板.

3.2 现象的描述及分析

在光源下观察双面刻划的亚克力板，可以看到如图5所示的现象：正等轴测图的像有明显的3D效果，而直线的像是两条分别位于直线两侧的曲线，如图5(b)所示.亚克力板将空间分成两个部分，只观察正等轴测图的像：当光源和人眼在同一侧(反射成像)时，可以看到一个立体的“CDUT”浮于板的表面，并且随着观察者和光源相对位置的改变，它会随之发生变化，如图5(a)所示；但当光源和人眼在不同侧(透射成像)时，仍旧能看到立体的“CDUT”，但这个像相对于之前的像是反转的，如图5(b)所示.同时还可以发现：当光源和人眼在不同侧(透射成像)时，可以同时看到正等轴测图的像和直线的像，如图5(b)所示；但当光源和人眼位于同侧(反射成像)时，只能看到靠近人眼和光源一侧表面划痕的像，如图5(a)所示.且与反射成像的图案相比，透射成像图案的亮度总是更低.

图5 两种刮擦全息图像的对比

在实验中观察到的刮擦全息图案，其实是由许多个亮点组成的，就像一个星系那样[3，4].这些亮点都位于圆弧形的划痕上，当圆弧小于半圆时，一个划痕上只有一个亮点，正如立体字母“CDUT”的正等轴测图那样[图5(a)]；而当圆弧是整圆时，一个划痕上有两个亮点，且这两个亮点关于此圆弧的圆心对称，正如直线的刮擦全息图那样[图5(b)].

对于某一个小于半圆的圆弧，当光源和观察者的位置确定后，此圆弧上一定存在一个满足折射定律的点.且当光源或观察者的位置发生变化时，这个点就会沿着圆弧滑动.由以上分析可知，可以用折射定律求出给定观察者、光源和圆弧圆心位置及其半径时亮点的空间位置.2.1中的数学模型就是以这个思路为基础建立起来的.

将图5(b)与图4(b)和(c)进行比较可发现，在2.1中建立的刮擦全息透射成像的数学模型是正确的.

3.3 两种透射成像方式的对比及分析

板有两个表面，所以透过板的光线发生了两次折射；而板的两面都可以刻有划痕，所以存在如图6所示的两种透射成像.

图6 两种透射成像的光路图

当光源靠近有划痕表面的一侧时，第一次发生折射的表面是某个划痕凹槽的一个切平面，第二次发生折射的表面是不带有划痕的一面，如图6中的光路G-B-C-F1所示；而当光源远离有划痕表面的一侧时，第一次发生折射的表面是没有划痕的一面，第二次发生折射的表面是某个划痕凹槽的一个切平面，如图6中的光路G-D-E-F2所示.两种情况下看到的全息图案都由透射成像产生，但第二种透射成像产生的图案是正的，而第一种透射成像产生的图案是反的(正反是相对于原图而言)，如图5(b)所示.当观察者隔着板在光源对面观察时，由于有两种透射成像方式的存在，板正反两面划痕的全息图案都可以被看到，如图5(b)所示.

在2.1中建立的数学模型，表面上只解释了第一种透射成像,但如果依据光路可逆原理[10]，将图2中光源和观察者的位置互换，就变成了第二种透射成像的数学模型.因此，2.1中的数学模型也适用于第二种透射成像.这样，这个数学模型就成功解释了两种透射成像方式.

4 刮擦全息透射成像与反射成像的对比

4.1 理论上的对比

由2.1和2.2中得出的最终结论可以看出，透射成像和反射成像的理论基础源于同一基本原理.因此,文献[6]对像的形变问题以及3D效果的成因等问题的解释同样适用于刮擦全息的透射成像.但由于k2的存在，二者的修正系数存在微小偏差.反射成像的光在进入观察者眼睛之前，经历了一次反射；而透射成像的光在进入观察者眼睛之前，经历了两次折射.因此，猜测两种成像方式的修正系数存在偏差是由于板有一定的厚度，且其材质的折射率与空气不同.后面将会从理论上推导出精度更高的k′，以证明这些猜测的正确性.

4.2 实验上的对比

刮擦全息透射成像与反射成像都会由运动视差产生3D效果，且图案都有发生形变的可能.与透射成像相同，反射成像也有两种反射形式，如图7所示.但在实验中，透射成像能观察到两种成像形式，而反射成像只能观察到一种成像形式，且这一种反射成像的全息图案比两种透射成像的全息图案都要明亮.下面对这两点现象提供解释.

由于黑色亚克力板良好的吸光特性，透过板的光都会发生衰减.如图7中的光路G-B-F1所示，第一种反射成像发生时，光在进入观察者眼睛之前，不须要穿过黑色亚克力板；而如图6的两条光路图所示，两种透射成像发生时，光在进入观察者眼睛之前，都必须要穿过黑色亚克力板一次.因此，第一种反射成像的图案比两种透射成像的图案都要更加明亮.如图7中的光路G-C-D-E-F2所示，光在对远离光源的划痕进行反射成像时，必须穿过板两次，这样进入观察者眼睛的光便发生了更大程度的衰减.因此，只有一种反射成像形式能被观察到，而两种透射成像形式都能被观察到.

图7 两种反射成像的光路图

5 透射成像修正系数k′的较精确推导

设

(n-y0-Rsinθ)j+(p-z0)k=

gxi+gyj+gzk

(b-y0-Rsinθ)j+(c-z0)k=

fxi+fyj+fzk

n=nxi+nyj+nzk

e=hk

(1)求精度较低的θ

将k′≈k代入2.1中的式(15)可求得精度较低的θ.最终要用到θ2′，但我们可以先引入一个精度较低的θ2′.

(2)求精度较低的θ2′

(20)

将式(20)中的两式联立，消去θf，可以求得精度较低的θ2′.

(3)求θn

由图2可得

(21)

引入

由2.1中的式(6)得

(22)

而由图2可得

(23)

将式(23)代入式(22)得，n的各分量为

(24)

因此

(gxcosθ+gysinθ)+2kagzcosθ2′

(25)

将式(25)代入式(21)得

(26)

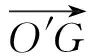
(4)求θ1

由图2可得

θ1=θg-θn

(27)

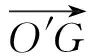
(28)

将式(26)求得的θn和式(28)求得的θg代入式(27)可求得θ1.

(5)求θ2

由折射定律得

n1sinθ1=n2sinθ2

(29)

将两介质的折射率和(4)中求得的θ1代入式(29)可求得θ2.

(6)求精度较高的θ2′

由图2可得

θ2′=θ2+θn

(30)

将(3)中求得的θn，(5)中求得的θ2代入式(30)可求得精度较高的θ2′.

(7)求k2

由2.1中的数学模型可知

(31)

(8)求精度较高的k′

将(7)中求得的k2，及

代入k′=k+k2，可最终求得精度较高的k′.

在以上8步推导中，有一些量作了近似处理，因此最终只是推导出了精度较高的k′.但由这些推导可以看出，刮擦全息透射成像修正系数k′与反射成像修正系数k的差别，是由k2的存在造成的，而k2受板材折射率和厚度的影响，因此4.1中的猜测是正确的.

6 结束语

本文依据几何光学的基本原理为刮擦全息的透射成像建立了理论基础，阐述了刮擦全息透射成像的基本规律.依据数学模型建立的计算机仿真效果，同实验现象相符，从而验证了理论的正确性.结合实验和理论，指出了透射成像与反射成像的相同与不同之处.刮擦全息透射成像理论的建立弥补了刮擦全息理论在这方面的缺失，进一步完善了基于几何光学的刮擦全息理论.刮擦全息透射成像使人们对这种全息成像技术有了更完整的认识，而透射成像存在两种成像方式的特殊性，必将使刮擦全息技术有更广阔的应用前景.对刮擦全息透射成像的研究，为基于刮擦全息的艺术创作提供了新的思路和理论指导.

1 朱伟利，孙雨南，陶世荃,等.光学信息技术原理及应用.北京：高等教育出版社,119～126

2 Eugene Garfield. ISI’s “World Brain” by Gabriel Lieb-ermann: The World’s First Holographic Engraving[A]. Essays of an Information Scientist[M], Vol 5, p.348-354, 1981-82 Current Contents, #52, p.5-11, 1981

3WilliamJBeatty.Makingahologramfromscratch.LaserFocusWorld, 2003, (March)24-25.

4WilliamJBeatty.Drawinghologramsbyhand[A];Pr-oceedingsofTheSocietyofPhoto-OpticalInstrumenta-tionEngineers(SPIE)[C], 2003

5MathewBrand.Specularholography.AppliedOptics, 2011, 50(25): 5042～5046

6 王鹏飞,钟慧,肖镇生,等.刮擦“全息”的理论解释和实验验证.大学物理,2015,8(8): 43～47

7PlummerWT,GardnerLR.AMechanicallyGeneratedHologram.AppliedOptics, 1992, 31(31): 6585～6588

8AugierángelG.，SánchezRaúlB.Hologravureasacom-puter-generatedandlaserengravedscratchhologram.OpticsCommunications, 2011, 284(1): 112～117

9 郭硕鸿. 电动力学.北京：高等教育出版社, 2008.117～118

10姚启钧. 光学教程.北京:高等教育出版社, 2014.115～116

11李丽.现代工程制图.北京:高等教育出版社,2009.101～106

TheStudyonTransmittedImaginginAbrasionHolography

XueRuiZhaoLeiWangTaoChengJianzhong

(DepartmentofAppliedPhysics,ChengduUniversityofTechnology,Chengdu,Sichuan610059)

To make up for the deficiency of transmitted imaging in abrasion holography, theoretical explanations based on geometrical optics are presented. Then these explanations are verified by a series of experiments in which acrylic plates with different scratched grooves on either sides were adopted. By comparing and contrasting transmitted imaging with reflected imaging in abrasion holography, theoretical and experimental similarities as well as differences of these two types of imaging are put forward. After that, a revisal modulus in the theoretical analysis of transmitted imaging with higher accuracy is deduced, which indicates that transmitted imaging is affected by the material and thickness of the scratched plate. Ultimately, the practical utility of transmitted imaging and its importance to the perfection of abrasion holography is illustrated.

abrasion holography; transmitted imaging; reflected imaging; refraction; acrylic glass

*成都理工大学物理学教学创新团队NO：JXTD201301四川省2014-2016年高等教育人才培养质量和教学改革项目.

薛瑞(1996- )，男，在读本科生.

程俭中(1957- )，男，副教授，主要研究方向为物理与物理教学.

2016-07-07)