Delta并联机器人非线性工作空间下轨迹插补算法*
陈 梅,石文博
(合肥工业大学 电气与自动化工程学院,合肥 230009)
Delta并联机器人非线性工作空间下轨迹插补算法*
陈 梅,石文博
(合肥工业大学 电气与自动化工程学院,合肥 230009)
为了提高Delta并联机器人运动控制精度,对其工作空间内非线性分布和轨迹插补算法进行了研究。基于仅考虑算法误差前提下,提出了通过选择Delta并联机器人单步插补位置误差最小的精度最优算法。基于机器人运动性能指标下的快速性和精确性,分析对比机器人传统插补算法和精度最优算法各自性能指标,最后通过Matlab平台仿真测试了算法的可行性,结果表明精度最优控制算法在整个机器人可达工作空间内都能有效提高机器人运动控制精度,控制效果要优于传统PVT控制方法。
并联机器人;工作空间;轨迹规划;空间插补;误差控制
0 引言
自从柔性自动化生产线得到大规模应用,并联机器人以其快速性、稳定性和准确性被广泛应用于分拣、包装、抓取、装配等领域。并联机器人由动平台、静平台、主动臂、从动臂构成,其运动特点是每个手臂由独立驱动器输入,最终又因共同约束而得到唯一输出,具有刚度大、承载能力强、精度高、自重负荷比小及动力性能稳定等一系列优点。由于传统Delta并联机器人空间插补算法,在快速性和精度上都没有达到系统可实现的最高性能指标,在针对Delta这种非线性强耦合机构时,传统插补算法很难实现高精度和快速性要求。分析Delta并联机器人单步插补运动状态,通过不同的插补策略,在精度控制和快速性控制上都可有相应改善。
1 Delta并联机器人介绍
1.1 并联机器人运动学
Delta并联机器人结构如图1所示,通过三根摆杆(主动臂)的上下摆动,实现动平台末端位置的控制。Delta并联机器人运动学求解分为正解和反解两个部分,一般采用解析法[1-2]或几何法[3]。

图1 并联机器人结构
1.2 Delta并联机器人非线性分析


表1 Delta并联机器人参数

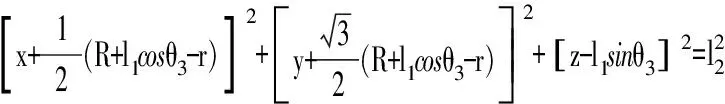
(1)

图2 并联机器人工作空间
2 传统算法
2.1 传统空间插补
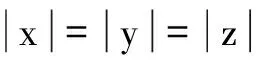
2.2Delta并联机器人传统路径规划
现阶段,并联机器人路径规划一般采用PVT(位置速度时间)控制方式[5-6],以空间直线插补为例,从空间中As点运动到Ae点,根据控制所需精度将直线lAs-Ae按速度控制分为若干小段,如图3中实线上圆点所示,通过并联机器人反解分别求出As.A1.A2…Ai.Ai+1…Ae位置时三个电机的控制角度,计算每次角度变化。通过对驱动电机输入相应变化角度,控制动平台从As点运动到A1…Ai点,最后运动到Ae点。而实际反解得到的电机角度受制于电机的控制精度,实际控制效果如图3中虚线所示,电机角度变化如图4所示。由于Delta并联机器人工作空间内可达到的点的非线性分布,越处于空间边缘处其可控精度越低,如图3所示,A、B、C三个区域最高控制精度是不同的,因此现有的PVT插补精度理应是实时变化的,否则无法达到整套系统的最高可控精度。
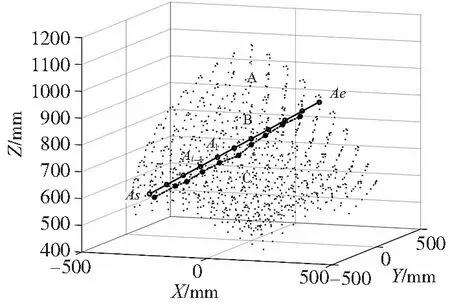
图3 并联机器人控制精度非线性分布

图4 并联机器人传统算法电机角度控制
3 单步精度最优控制算法
并联机器人由三个电机控制,每一时刻单个电机可有三种状态(正转、停止、反转),对整个机器人而言每一时刻都有27种状态,单步运行下有27种运动方向,分别运动到空间中的不同位置,当三个电机都是停止状态时,机器人末端位置则不会变化,该状态称为机器人停止态。如图5所示为并联机器人单步控制下从同一位置出发,下一时刻可到达位置,经分析对比,并联机器人单步27态图在空间不同位置会发生不同程度畸变,即27态图是不固定的。

图5 并联机器人单步27态图
3.1 单步最优控制
单步最优控制为预测机器人下一步可达的27种位置,在27种结果中选取最合适的的作为最优策略,有时间最优策略[7],能量最优策略[8],本文主要采取位置最优控制,其中判断27种策略的优劣性在该算法中至关重要。
单步最优控制流程图如图6所示,首先更新机器人末端位置,以该位置为中心,预测出下一步27种可能到达的位置,通过计算每一种可能性下的位置误差,选取位置误差最小的一组作为机器人下一步的执行策略,然后重新更新机器人位置,直到到达终点。
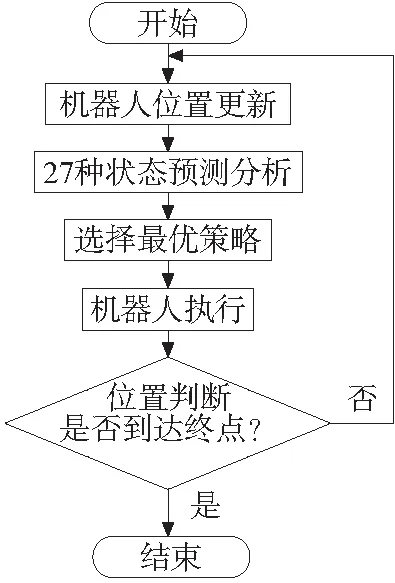
图6 单步预测控制算法流程图
为衡量不同位置状态下误差的大小,需对衡量标准作出如下两条定义:
定义一:点到直线的距离为过该点作垂直于直线的垂线,点到垂足的距离记为点到直线的距离,如图7中dline所示。
定义二:点到圆弧的距离为该点到连接该点与圆心的直线在圆面上的投影与圆弧的交点的距离,如图7中dcircle所示。
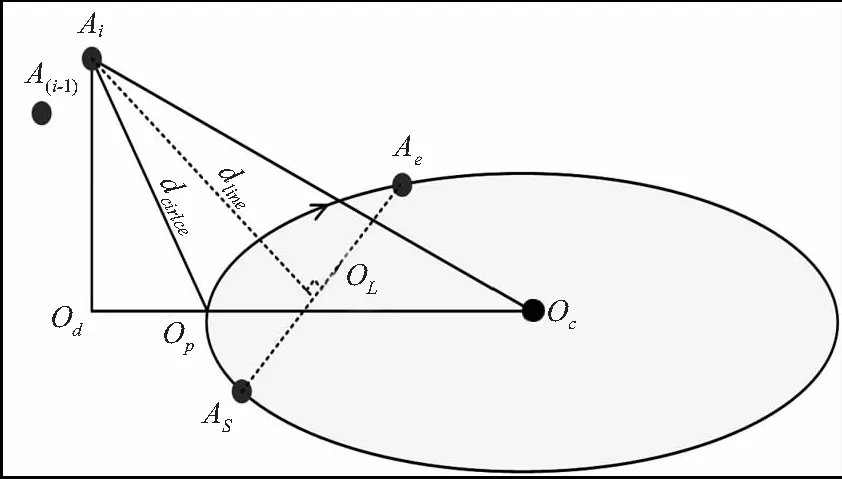
图7 空间点到直线、圆弧距离

3.2 速度控制
无论是单步最优控制策略还是混合控制策略,它们都是位置速度独立控制策略,优先进行位置精度控制,在位置精度达到期望的前提下进行速度控制,一般应用于脉冲与频率协同控制方式的电机。脉冲个数决定电机运动量,脉冲频率决定电机运动速度。由单步预测位置控制模式可以得到各电机的脉冲序列,通过控制脉冲频率实现电机输出转速的控制。以空间直线运动为例,从空间起点运动到终点,若要求机构按照S型曲线[9]先加速后减速运动到终点,此时需要按期望设定频率-时间变化曲线。由于位置与速度分离控制,在位置控制完成的基础上速度控制便更为简单,只需要设计合理的速度控制曲线即可使得系统运动更加平稳。如文献[9]中提出的S型加减速七段设计方法,在现阶段机器人速度控制[10]中广泛应用。
4 控制效果分析对比
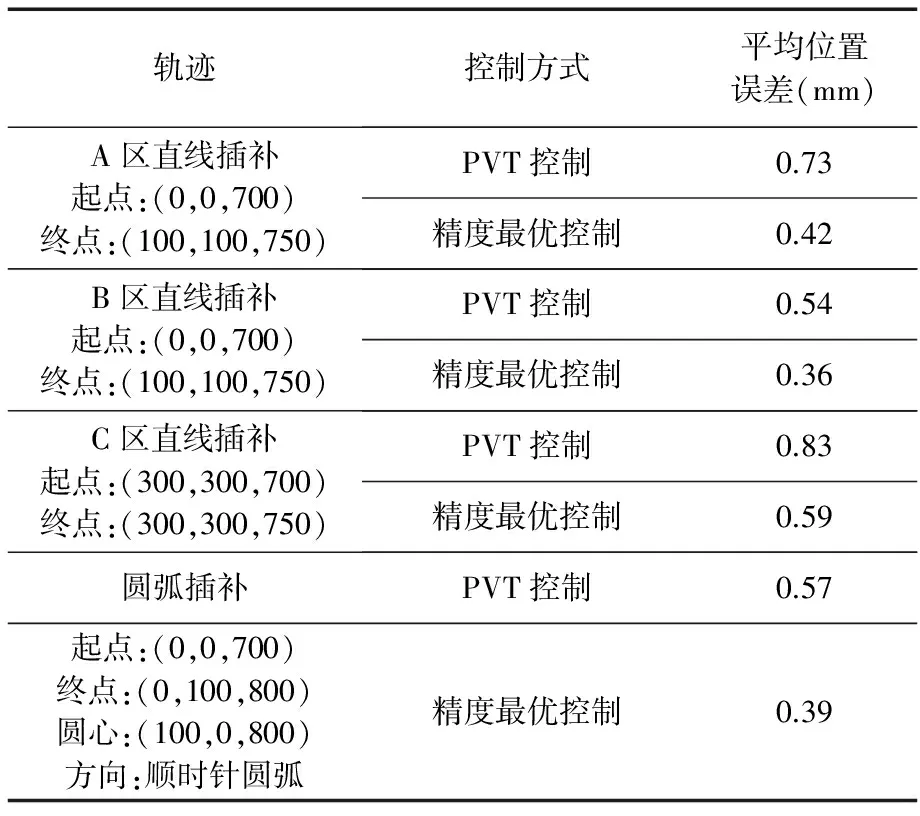
表2 运动指标结果对比

图8 空间直线插补
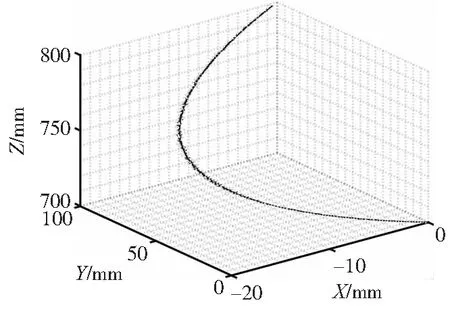
图9 空间圆弧插补

图10 空间圆弧插补电机角度变化
5 结论
针对并联机器人耦合非线性特点,虽然传统PVT控制可以满足系统精度要求,但因为机器人工作空间的非线性分布,PVT控制精度存在大幅度波动,在非线性波动较为平缓的B区PVT控制可以取得较高的控制精度,但在A区和C区PVT控制精度时刻变化且精度不高。相比之下,单步位置精度最优控制可有效控制轨迹运动误差,在整个工作空间下都能完成高精度控制。
[1] 郭超. 高速并联机器人及其控制系统研究[D]. 淄博:山东理工大学,2014.
[2] Mustafa M, Misuari R, Daniyal H. Forward kinematics of 3 degree of freedom Delta robot[C]// Research and Development, 2007. SCOReD 2007. 5th Student Conference on. IEEE, 2008:1-4.
[3] 蔡汉明, 马恒印, 段萌. Delta并联机器人运动空间的几何作图求解[J].装备制造技术,2013(5):31-32.
[4] Nabat V, Company O. Par4: Very high speed parallel robot for pick-and-place[C]// Intelligent Robots and Systems, 2005. (IROS 2005). 2005 IEEE/RSJ International Conference on. IEEE, 2005:553 - 558.
[5] 雷奶华,赵新华,杨玉维.3-RRRT并联机器人插补算法及其误差分析[J].天津理工大学学报,2005,21(1):50-53.
[6] 刘凉.3-RRRU并联机器人运动学控制的研究[D].天津:天津理工大学,2010.
[7] Gasparetto A,Zanotto V. A new method for smooth trajectory planning of robot manipulators[J].Mechanism and Machine Theory,2007,42(4):455-471.
[8] 殷国亮,白瑞林,王永佳,等.一种并联机器人的时间最优轨迹规划方法[J].计算机工程,2015,41(10):192-198.
[9] 刘鹏飞, 杨孟兴, 宋科,等.‘S’型加减速曲线在机器人轨迹插补算法中的应用研究[J].制造业自动化,2012,34(10):4-11.
[10] 黄海忠.DELTA 并联机器人结构参数优化与运动控制研究[D]. 哈尔滨:哈尔滨工业大学,2013.
(编辑 李秀敏)
Trajectory Interpolation Algorithm for Delta Parallel Robot in Nonlinear Working Space
CHEN Mei , SHI Wen-bo
(School of Electrical and Automation Engineering, Hefei University of Technology, Hefei 230009, China)
In order to improve the accuracy of motion control of Delta parallel robot, the non-linear distribution and path interpolation algorithm in its work space are studied.In only considering error of the algorithm premise, the precision optimal algorithm by choosing minimum error of single step interpolation position of Delta parallel robot is proposed. Based on the rapidity and accuracy under motion performance index of the robot, the performance index of the traditional interpolation algorithm and precision optimal algorithm is analyzed and compared. Finally, the feasibility of the algorithm is tested through Matlab simulation platform, and the results show that the precision optimal control algorithm can effectively improve the precision of the robot motion control in the whole work space where the robot can arrive and its control effect is better than traditional method of PVT control.
parallel robot;working space;trajectory planning; spatial interpolation; error control
1001-2265(2017)01-0074-04
10.13462/j.cnki.mmtamt.2017.01.020
2016-03-07;
2016-05-15
合肥工业大学产学研校企合作资助项目(12-069k;13-040k)
陈梅(1963—),女,合肥人,合肥工业大学副教授,研究方向为运动控制,(E-mail)zdhchen@126.com;通讯作者:石文博(1991—), 男, 安徽宿松人,合肥工业大学硕士研究生,研究方向为运动控制,(E-mail)hfut_swb@mail.hfut.edu.cn。
TH165;TG659
A

