时间分割圆弧插补算法的改进

李彦奎，吕彦明

(江南大学 机械工程学院，江苏 无锡 214122)

时间分割圆弧插补算法的改进

李彦奎，吕彦明

(江南大学 机械工程学院，江苏 无锡 214122)

插补算法是数控机床的重要组成部分，插补算法的优劣直接影响了机床的加工性功能。对于现有的时间分割圆弧插补方法大多采用的是近似计算，计算过程复杂，插补精度和插补效率相对较低。为提高机床的加工性功能，文章基于等弦高误差理论对原有的时间分割圆弧插补算法进行改进，改进后的插补算法计算简便，实现了插补过程的无近似计算，且使每一个插补点都落在插补圆弧上；在保证插补精度的条件下，因为在插补计算过程中采用了最大允许弦高误差，实现了插补效率的最大化。

等弦高误差；时间分割圆弧插补；计算简便；无近似计算；插补效率

0 引言

近年来我国机械制造业面临着自动化程度和加工效率较低等问题，为解决这一问题，国家把高档数控机床列入了中国制造2025的计划之中。在数控机床的计算机控制系统中插补算法是其最基本而又极为重要的组成部分，衡量插补算法优劣的两个主要指标：插补精度和插补效率。插补算法的优劣直接影响了机床的加工性能，为提高机床的加工性能，对插补算法的研究就变得极为重要。

“插补”是根据轮廓形状和进给速度的要求，对轮廓曲线的起点、终点之间的空间进行数据点密化，密化到点与点之间的距离为一个脉冲当量，以此控制各轴运动，从而形成要求的轮廓轨迹[1]。文章在前人的基础上对时间分割圆弧插补算法进行了研究。时间分割圆弧插补算法是用弦线逼近圆弧轮廓曲线，实现圆弧插补。对于时间分割圆弧插补算法的计算，目前大多数教材均采用近似算法[2-3]。很多学者也对该算法进行了一定的研究，孔德彭等[4]使用插值法在原有的两个插补点之间增加插补点，使插补点密化，提高了插补的精度。王忠[5]运用等价无穷小理论，将正切函数等价成步距角的一次函数，实现了计算过程的去三角化，简化了计算。也有学者通过三角函数和插补圆弧参数及步长之间的转换和基于等步长法，实现了插补的无近似计算[6-9]。在一定程度上提高了插补精度和效率。

以上时间分割圆弧插补算法是以步距角或步长为参数，且计算过程大多采用近似计算，计算过程较为复杂。为简化计算，提高差不效率，文章基于等弦高误差理论，在保证插补精度的条件下，采用最大允许弦高误差为参数，对时间分割圆弧插补算法进行改进。根据计算推导出了下一插补点和当前已插补点之间成线性关系，计算推导过程简便，实现了无近似计算，使得每个插补点都落在圆弧上；由于采用了最大允许弦高误差，使得插补步长最大化，进而使插补效率最大化。

1 时间分割插补法原理

如图1所示，A是当前已插补点，B是下一个插补瞬时点，其坐标分别为A(xi，yi)、B(xi+1，yi+1)。插补是指由已加工点A求出下一个待插补点B，实质上是求在一个插补周期内，沿x轴和y轴的进给增量Δx和Δy。图中弦AB是圆弧插补每个周期的进给步长l。AP是A点的切线，M是AB的中点E是AF的中点，且ME⊥AF,OM⊥AB。

图1 第一象限圆弧插补示意图

根据三角函数之间的转换可以得出：

(1)

式(1)反应了当前已插补点与增量Δx和Δy之间的关系，只要计算出Δx和Δy，就可求出新的插补点坐标,即：

(2)

关键是Δx和Δy的求解。由于式(1)中cosα和sinα都是未知数难以求解，所以必须采用近似计算的方法，用cos45°和sin45°代替式(1)中cosα和sinα，即：

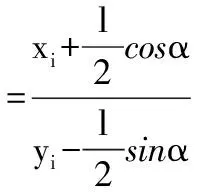
由关系式

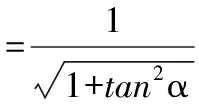
进而求得Δx：

Δx=lcosα

(3)

将式(3)代入式(1)可求得Δy。

求出沿x轴和y轴的进给增量Δx和Δy，根据式(2)可求得新的插补点坐标。

此方法的缺点就是采用了近似计算，造成了速度的波动，另外在计算坐标增量时要进行反复迭代，计算复杂，浪费时间，降低了插补效率。

2 等弦高误差原理

等弦高误差是指：对于一条曲线,其理论轮廓曲线与每段实际插补曲线之间的最大间距相等[10-11]。如图2已知理论曲线Q(x,y)，起点P(x0，y0)和给定最大允许误差为δ，求曲线Q(x,y)上的插补点P1，P2……Pn。过点P0作一半径为δ的圆，作圆与理论曲线的公切线MN。切点分别为M(xm,ym)，N(xn,yn)。

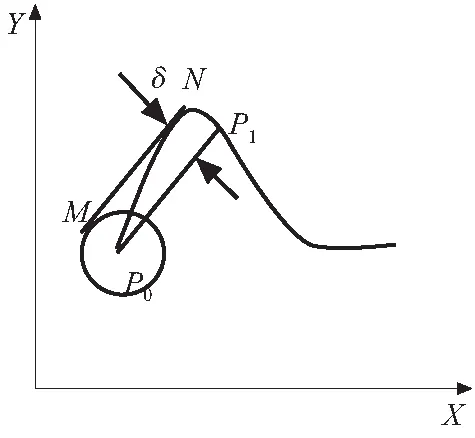
图2 等弦高误差原理示意图

(1)求公切线斜率

A样品空白对照——25 μl样品+25 μl底物（37 ℃孵育10 min）+50 μl蒸馏水（37 ℃下孵育 60 min）+100 μl醋酸-醋酸钠缓冲溶液；

设公切线MN的斜率为kmn，则:

(4)

由已知条件知：

(5)

四个方程,四个未知数,由式(4)和式(5)求出kmn。

(2)求插补点

已知公切线斜率kmn，直线P0P1过点P0且与Q(x,y)相交，其交点就是所求点P1。根据方程：

求得新的插补点坐标P1点。然后根据当前求得的插补点再求下一个插补点，以此类推。在保证插补精度的条件下，由于采用了最大允许插补弦高误差，使插补进给步长最大化，该方法实现了插补效率的最大化。

3 改进的时间分割圆弧插补算法

如图3所示，以第一象限逆时针圆弧插补为例。已知被插补圆O的半径为R，插补起点P0(x0，y0)，允许的最大加工误差为δ。求下一个插补坐标点P1，P2……Pn。过点O作半径为(R-δ)的同心圆，过点P0作小圆的切线，切点为N(xn，yn)，交大圆于一点，该点就是所求的点P1。过点O作ON⊥P0P1，交大圆于点M，所以MN=δ。

图3 插补示意图

(1)求N点坐标

(6)

由式(6)得：

(2)求P1点坐标

因为N是P0P1的中点，所以：

由此可以得出：

x1=Ax0-By0y1=Ay0+Bx0

因为A，B是常数，由上式得出了下一插补点和当前插补点的线性关系，在插补前可以将A，B值预先算出，在插补过程中对A，B进行赋值，从而避免了采用近似计算造成的速度波动和计算过程的反复迭代。使得插补计算过程变得简便，且每一个插补点都落在圆弧，提高了插补效率。由于在插补过程中采用最大允许弦高误差，即实现了插补进给步长的最大化，最大程度的提高了插补效率。

4 插补实例

利用VB对半径为50mm的圆弧在第一象限内作逆时针插补，插补的起点为(50,0)，终点为(0,50)，最大允许弦高误差为0.02。图4是以最大允许弦高误差为参数的插补计算过程；图5是以步距角为参数，步距角为0.04，利用等价无穷小将三角函数转化成步距角的一次函数的插补计算过程[5]，其步长f和步距角θ应满足式(7)和式(8)：

(7)

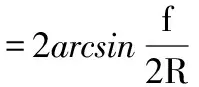
(8)

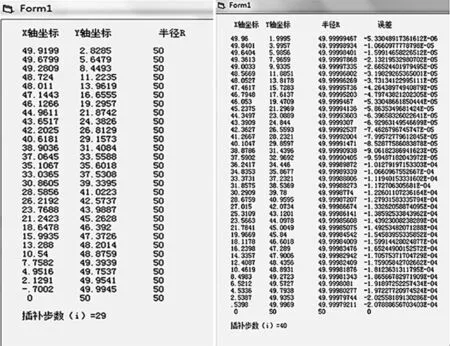
图4 插补计算过程 图5 插补计算过程

在圆柱形零件加工的过程中，我们已知被加工零件的最大允许加工误差。在该例中，当我们直接运用最大允许加工误差为参数进行插补计算时，实现了插补步长的最大化，所用的插补步数为29步；当我们以步距角为参数时，根据式(7)先估算出步长，再由式(8)根据步长算出步距角进行插补计算时，所用步数为40步。由于同类机床的插补周期相同，例如在FANUC7M系统其插补周期为8ms，故在满足精度的前提下，前者的插补效率优于后者。

5 结论

由理论推导和实例模拟分析得出以下结论：

(1)根据计算推导出了相邻已插补点和下一插补点之间的关系，二者成线性关系。计算过程无近似计算，使得每一个点都落在圆弧上。

(2)采用最大弦高误差为参数，避免了繁琐的计算，使计算过程更加简便，无累积误差。

(3)在时间分割圆弧插补计算过程中，直接运用最大弦高误差为参数进行插补运算，实现了插补步长的最大化，进而最大程度的提高了插补效率。

[1]SpirosGPapaioannou.Interpolationalgorithmsfornumericalcontrol[J].ComputersinIndustry, 1979(1):27-40.

[2] 何雪明，吴晓光，常兴.数控技术[M]. 湖北：华中科技大学出版社，2006.

[3] 杜君文.数控技术[M].天津：天津大学出版社，2002.

[4] 孔德彭，张国平，张玉姣.基于圆弧插补的时间分割插补算法改进[J].机械与电子，2010(2):33-37.

[5] 王忠.时间分割圆弧插补新算法[J]. 组合机床与自动化加工技术,2006(5):33-34.

[6] 周慧.数据采样法圆弧插补的新算法[J].组合机床与自动化加工技术,2004(2):40-41,44.

[7] 李莉，冯志永.数控系统中圆弧插补算法的改进和实现[J]. 组合机床与自动化加工技术,2009(7):61-65.

[8] 张永刚.时间分割圆弧插补的新算法[J].机械制造与自动化，2015(2):63-64.

[9] 伍胡平，周亚军.数据采样插补算法的研究[J].组合机床与自动化加工技术,2008(9):13-15,19.

[10]YJLin,TSLee.Anadaptivetoolpathgenera-tionalgorithmforprecisionsurfacemachining[J].Computer-AidedDesign, 1999,31:237-247.

[11] 牛文铁,胡德计,徐燕申,等.数控加工中定曲线方程轮廓的等弦高误差拟合算法研究[J].制造业自动化,2001(9):7-11.

(编辑 李秀敏)

Improvement of Time Segmentation Arc Interpolation Algorithm

LI Yan-kui，LV Yan-ming

(School of Mechanical Engineering，Jiangnan University，Wuxi Jiangsu 214122，China)

Directly affecting the machining features of CNC machine tools, interpolation algorithm is an vital part of CNC machine tools.For the existing most of time segmentation arc interpolation algorithms the process of calculation are complex and approximate calculation is adopted.In order to improve the machining features, based on the theory of equal chord deviation error the original time segmentation arc interpolation algorithm is improved in the paper and the improved arc interpolation algorithm which is simple achieves the interpolation process of no approximate calculation and each interpolation point falls on the interpolation arc. Under the co- ndition of guaranteeing interpolation accuracy, because of the maximum allowed chord deviation error used in the process of interpolation calculating , the maximization of the interpolation efficiency is come true.

equal chord deviation error;time segmentation arc interpolation;simple calculation;no approximate calculation; interpolation efficiency

1001-2265(2017)01-0016-03

10.13462/j.cnki.mmtamt.2017.01.005

2016-03-18；

2016-04-15

李彦奎(1989—)，男，河南商丘人，江南大学研究生，研究方向CAD、CAM，(E-mail)1091018151@qq.com；通讯作者：吕彦明(1989—)，男，山西和顺人，江南大学教授，博士，研究方向为CAD、CAM。

TH16;TG65

A