复杂曲面测量机器人运动学分析及测量路径规划研究

马国庆，刘 丽，张若妍，于正林，曹国华

（长春理工大学 机电工程学院，长春 130022）

复杂曲面测量机器人运动学分析及测量路径规划研究

马国庆，刘 丽，张若妍，于正林，曹国华

（长春理工大学 机电工程学院，长春 130022）

以往的机器人测量系统基本上都是通过手眼标定来提高系统的精度，受各方面的影响因素较大，提出一种利用IGPS来实时获取工业机器人末端测量传感器在全局坐标系下的位置，通过轨迹规划技术保证测量轨迹时刻和被测工件表面法向相一致，为复杂零件的深孔形貌测量及基于全局位置的点云拼接奠定了基础。分析了测量机器人的运动学关系，通过仿真和实验验证了轨迹规划的正确性。

复杂曲面；测量机器人；运动学分析；测量路径规划

0 引言

随着现代生产的复杂化、精密化，具有复杂曲面外形的产品也越来越多，且对零件的结构和外形的要求也越来越高，尤其是在航空航天、汽车、航海、武器装备、模具制造等领域，复杂曲面外形的零件比比皆是[1]。目前，能够实现曲面测量的手段大致可以分为以下四种：一是以三坐标测量机、关节式测量臂为代表的接触式曲面测量方法[2]；二是以手持式三维扫描仪、摄影测量系统、超声测量系统为代表的非接触式曲面测量方法[3]；三是以工业CT法和核磁共振法（MRI）为代表的逐层扫描测量方法[4]。四是以工业机器人与非接触扫描设备相结合构成的扫描测量系统[5]。以往的机器人测量系统基本上都是通过手眼标定来提高系统的精度，受各方面的影响因素较大，本文提出一种利用IGPS来实时获取工业机器人末端测量传感器在全局坐标系下的位置，通过轨迹规划技术保证测量轨迹时刻和被测工件表面法向相一致，为复杂零件的深孔形貌测量及基于全局位置的点云拼接奠定了基础。

1 机器人测量系统组成

机器人测量系统包括Motoman-HP20D六自由度工业机器人、IGPS（indoor GPS）全局定位系统、测量传感器系统、计算机辅助系统、安全防护系统、电控柜等辅助系统组成；软件系统主要包括机器人控制模块、传感器控制模块、路径规划软件、数据采集与分析模块、通讯模块和其他模块等，软件系统实现各个硬件系统的联合控制。

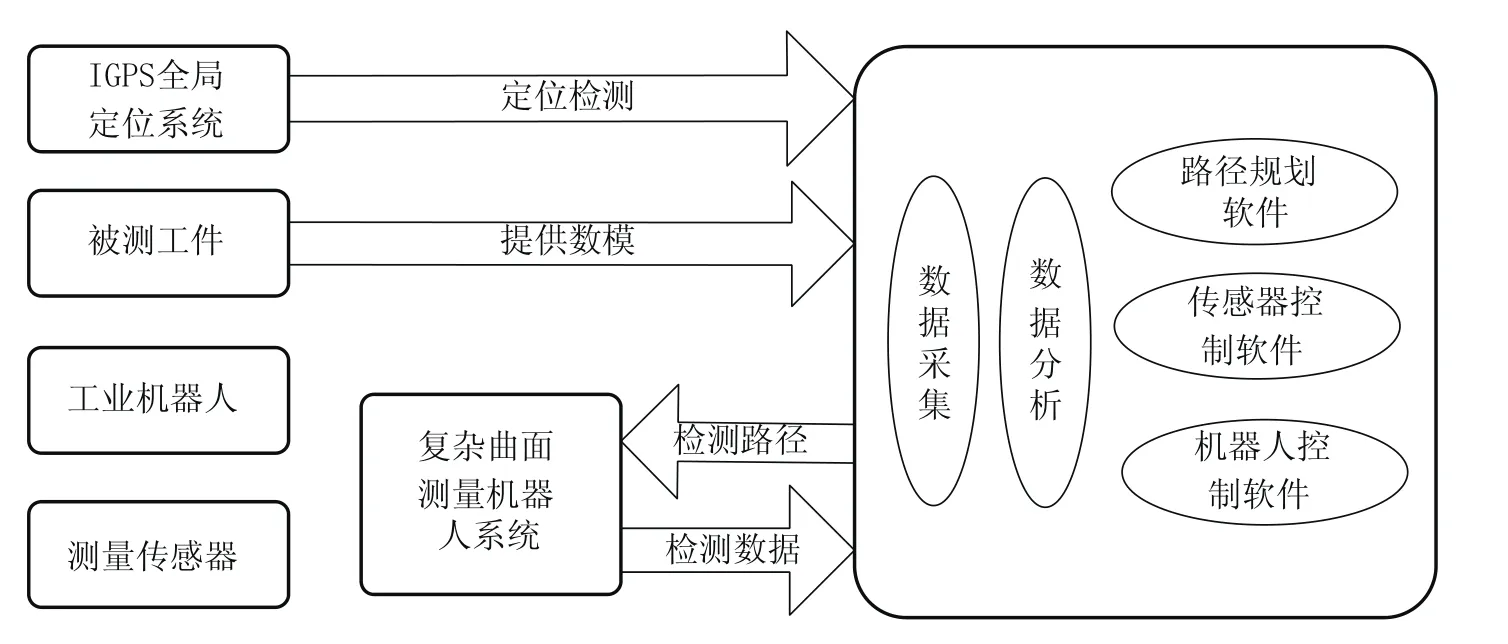
图1 机器人测量系统组成图

2 测量机器人运动学求解

运动学的求解过程并不考虑各杆件之间的相互作用力，只研究其运动的关系。正运动学问题是在已知各关节角及杆件尺寸的基础上，求解机器人末端执行器在基坐标系下的位姿，其实质是运动学方程式的建立和求解。逆运动学问题恰恰相反，是在已知杆件的几何参数和末端执行器相对于基坐标系的期望位姿，求取机器人末端执行器达到此位姿时各关节的角度值[6]。

2.1 连杆坐标系建立

HP20D是一款具有6个旋转关节的串联机器人，为清晰地表明该机器人各连杆之间的位姿关系，可采用D-H坐标变换法[7]进行建模，建模原则如下：

1）绕Zi-1轴旋转θi角，使Xi-1轴与Xi同一平面内；

2）沿Zi-1轴平移距离di，把Xi-1与Xi同一直线上；

3）沿Xi轴平移距离ai，把连杆i-1的坐标系移到使其原点与连杆i的坐标系原点重合；

4）绕Xi-1旋转ai角，使Zi-1轴转到与Zi同一直线上。

HP20D机器人D-H坐标系如图2所示。

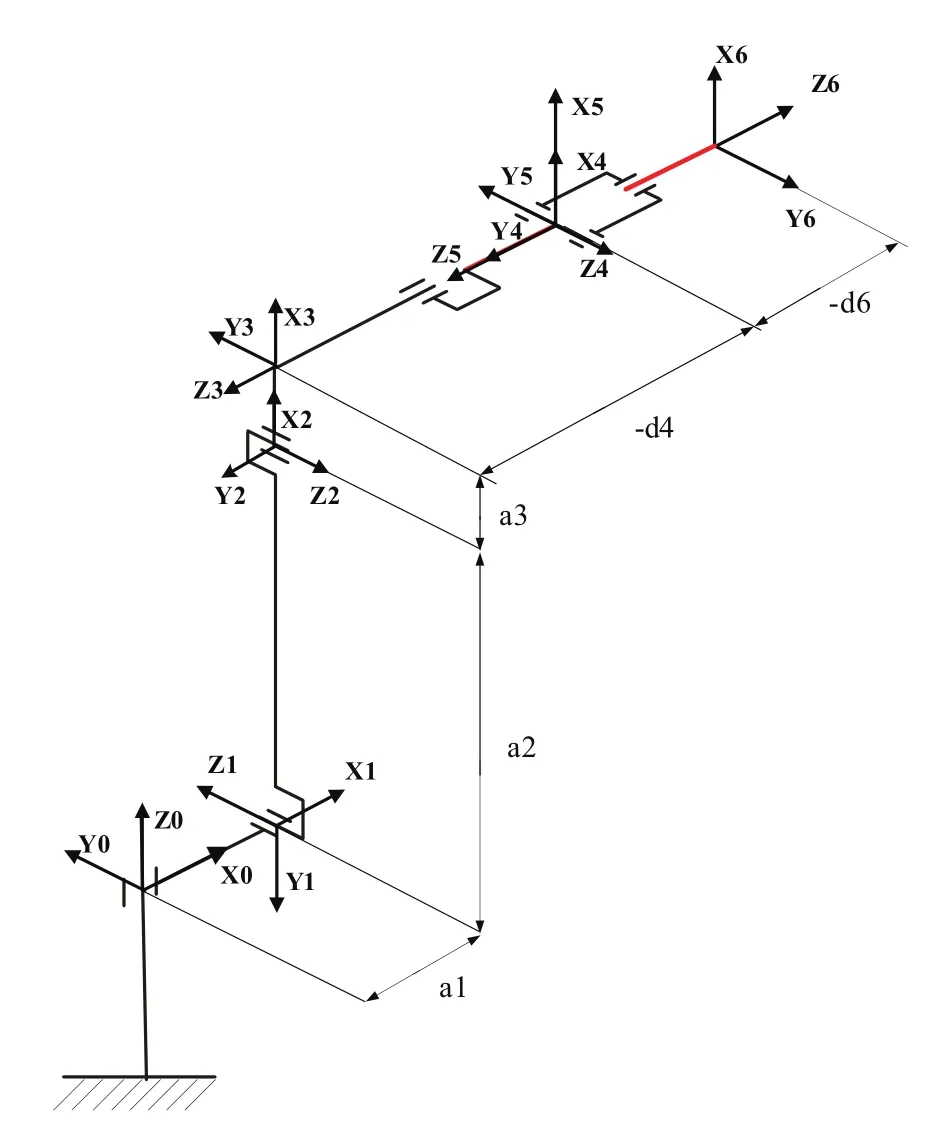
图2 HP20D机器人D-H坐标系

2.2 正运动学求解

建立各关节坐标系后，根据相邻关节坐标系间的转换关系，可确定关节和连杆的D-H参数，HP20D机器人的各个关节均为转动关节，所以只有关节角θ是变量，关节扭角α、连杆长度a、连杆距离d均为固定值，HP20D机器人D-H参数如表1所示。

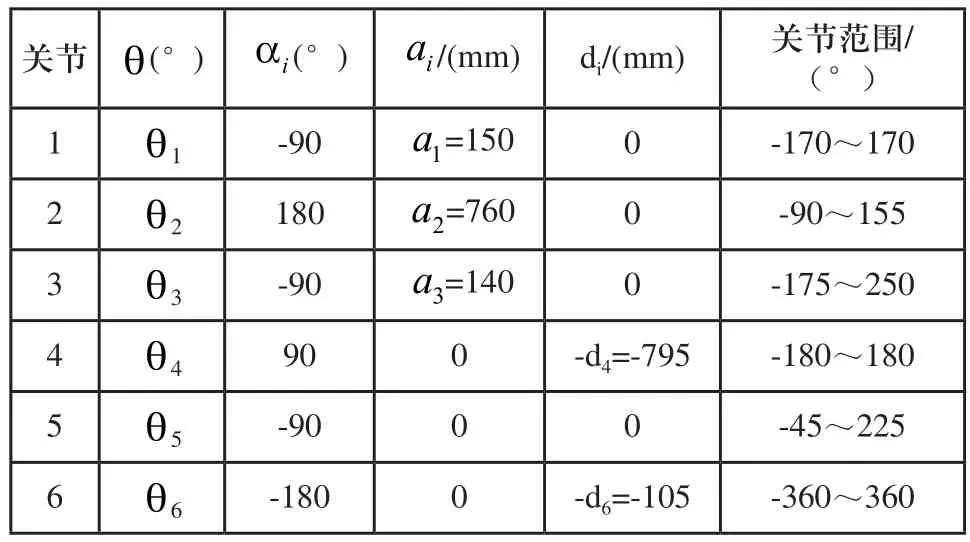
表1 Motoman-HP20D 机器人的连杆参数

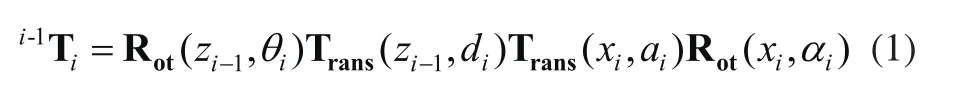
上式用矩阵形式表示如下：

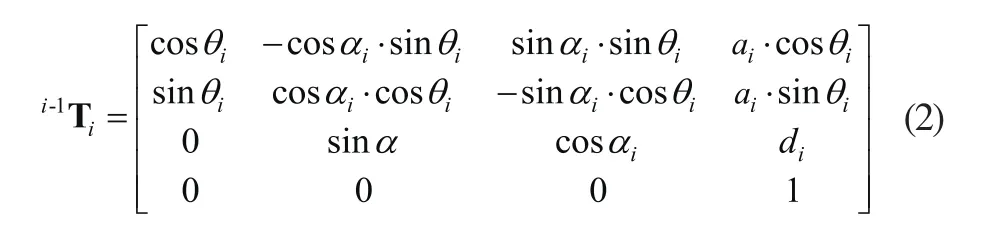
将表1中参数代入式(2)，求得坐标变换矩阵：

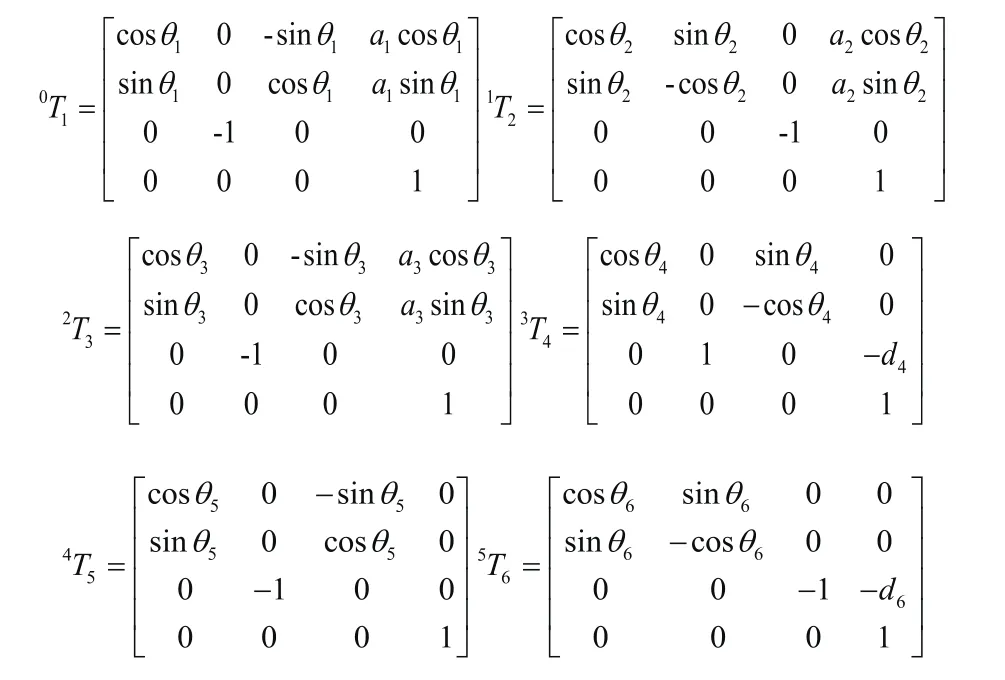
根据式(2)的D-H变换矩阵，可得机器人末端相对于基础坐标系的变换矩阵：

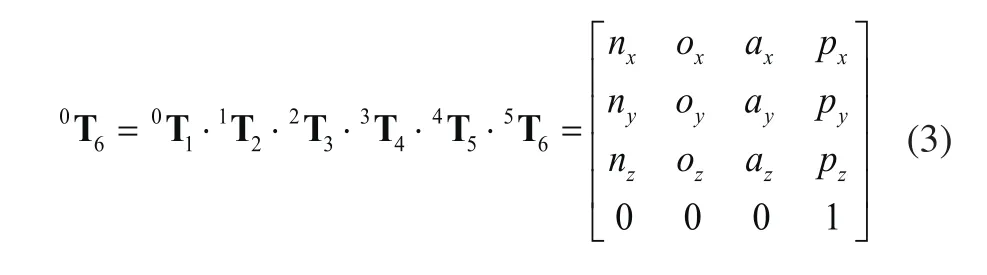
因此，将机器人的各个坐标转换矩阵代入式(3)，求得HP20D机器人正运动学方程。

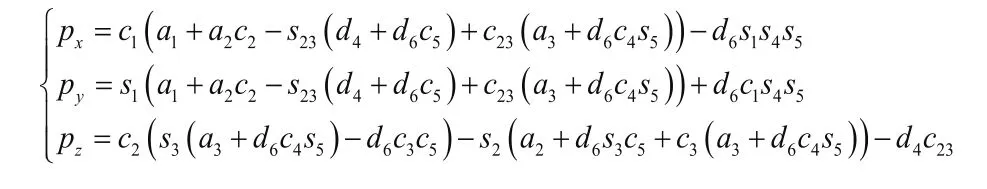
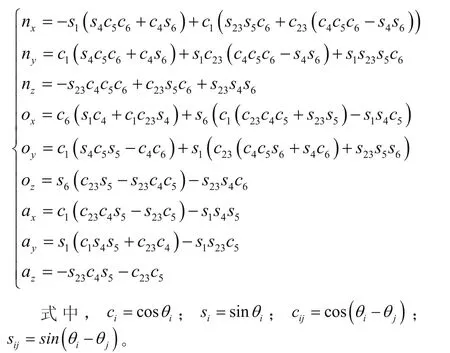
2.3 逆运动学求解

对于给定的机器人末端执行器的位姿，HP20D机器人的构型决定了其存在多种手臂形态，运动学的逆解并不唯一，即运动学逆解具有多解性，在求解过程中采用双变量正切函数表示关节变量，避免出现解丢失的可能性。

将式(3)变形为：

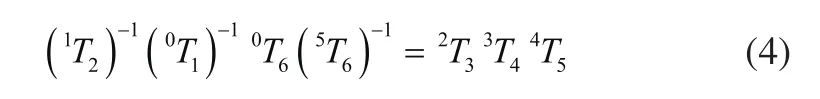
令：

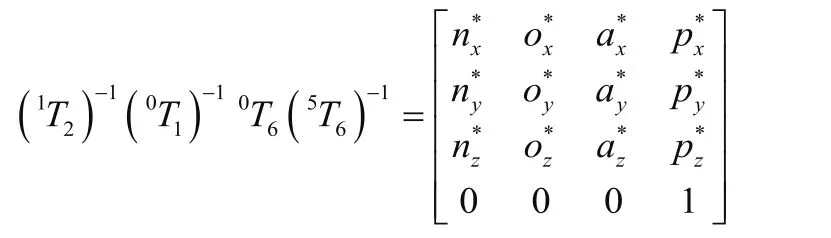
其中：

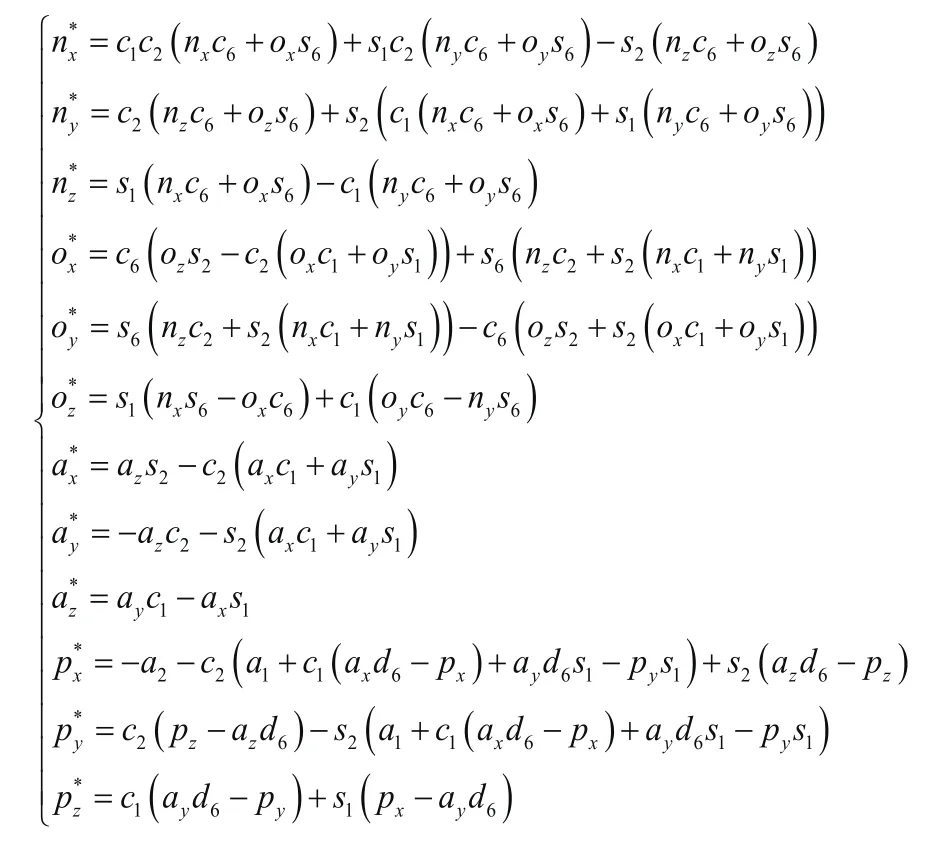
则式(4)的右边：

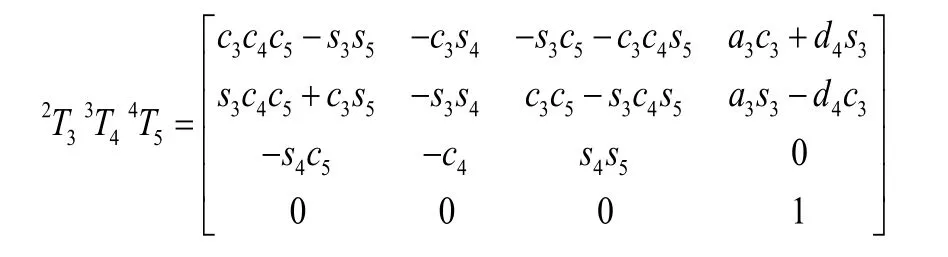
1）求解θ1

由式(4)中等式左右两边矩阵第三行第四列元素相等可得：

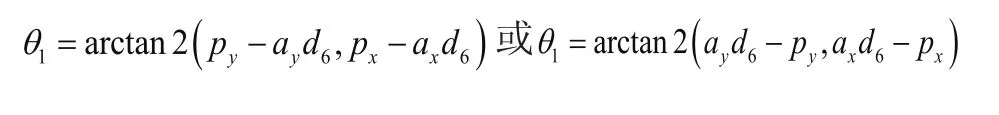
2）求解θ2

由式(4)中等式左右两边矩阵第一行第四列元素和第二行第四列元素分别相等：

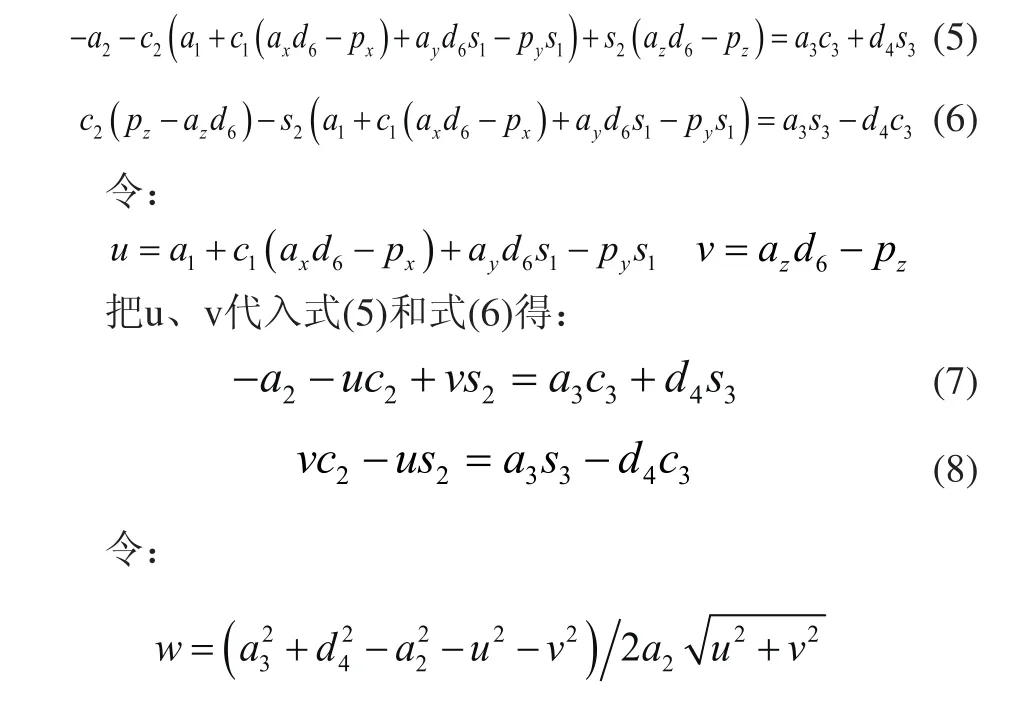
将式(7)和式(8)两边平方然后相加化简得到：

3）求解θ3

式(7)和式(8)是关于s3和c3的方程组，故可解得：

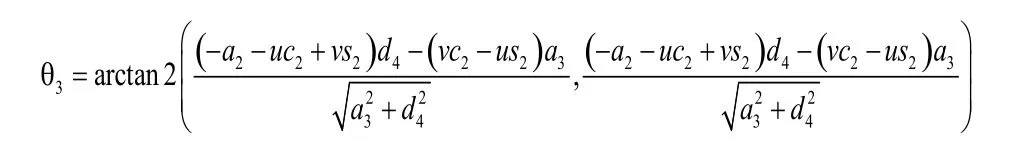
4）求解θ5

由式(4)中等式左右两边矩阵第一行第三列和第二行第三列元素相等得：

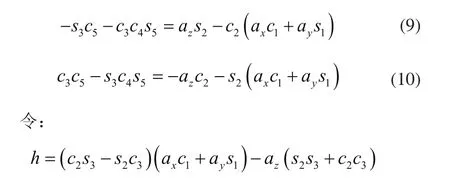
式(9)和式(10)两边分别乘以s3和c3，相减可得：

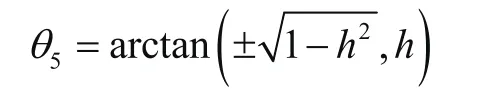
5）求解θ4

式(9)和式(10)两边分别乘以s3和c3，相减可得：

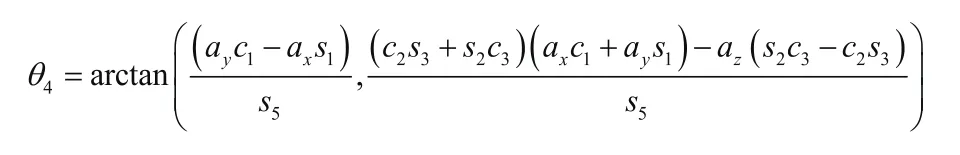
6）求解θ6

由式(4)中等式左右两边矩阵第三行第一列和第三行第二列元素相等得：

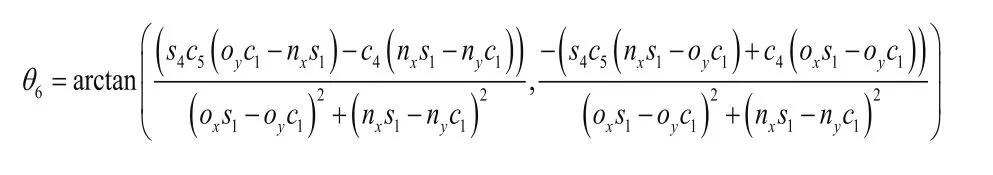
2.4 解的对应关系

在理论上通过逆解可得到机器人的8组关节角度值，但在实际的控制系统中，由于杆件间存在物理干涉以及运动连续性的要求，往往只存在一组最有的可行解。采用最短行程原则进行择优，其算法流程如图3所示，θcm表示机器人当前第m关节坐标，θnm表示机器人逆解第n组第m关节坐标，其中n=1,2,…,8；m=1,2,…,6。

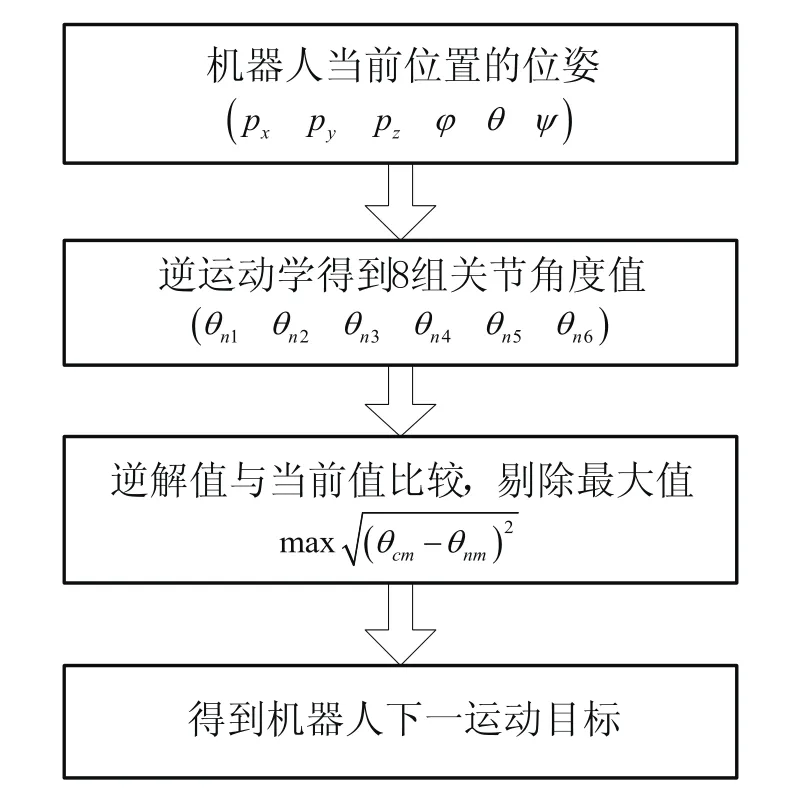
图3 最短行程原则算法流程图

3 测量路径仿真及程序生成

本测量系统测量的对象是曲率不断变化的大型复杂曲面类零件，且零件带有深孔，为了有效地扫描曲面及孔底的形貌，扫描仪工作时需满足如下约束条件，如图4所示。

Pi和Ni分别表示曲面上点和点的单位法向量，L表示激光扫描仪，Bi表示两激光边界扫描线的平分线。约束条件分析如下：

1）扫描仪倾角：

激光三角测量法扫描仪扫描的重要假设是出射光束与被测点处曲面法矢共线，但在实际测量的过程中，两者一般存在着一个θ夹角，且此夹角不能超过限定值。故扫描点Pi到扫描头L的连线扫描点法向量的夹角应小于约束角γ。

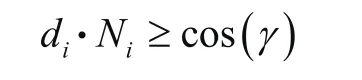
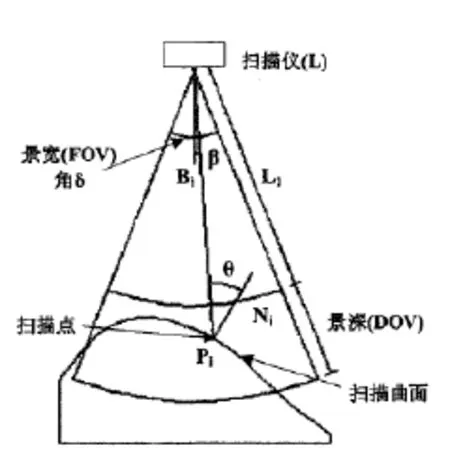
图4 扫描仪扫描约束

式中单位向量：

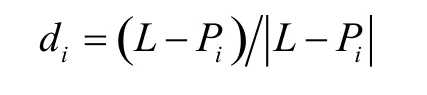
2）景宽（FOV）

扫描点应在对应某条激光条纹长度范围内，被测曲面上点到激光头的距离不同，不同位置的有效条纹扫描长度不断变化，与图4所示理想扫描情况不同，设(-di)与Bi之间夹角β：

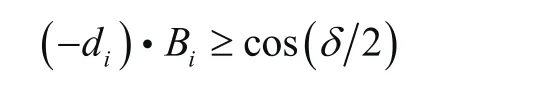
式中为景宽角，为激光扫描仪固定参数。

3）景深（DOV）

被测点必须在一个偏离激光源的指定范围内。

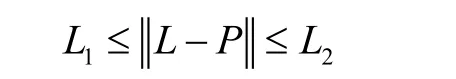
利用仿真软件，采用等间距采用等间距采样原则，完成路径测量路径，保证测量传感器时刻和被测表面法向相一致，仿真如图5所示。

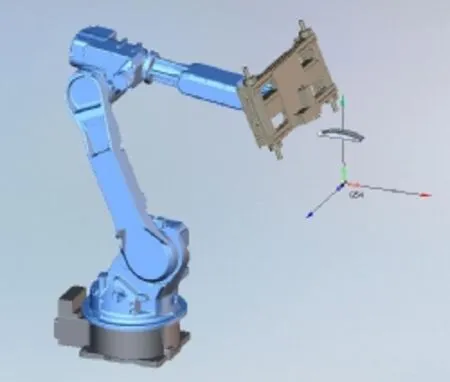
图5 曲面测量仿真

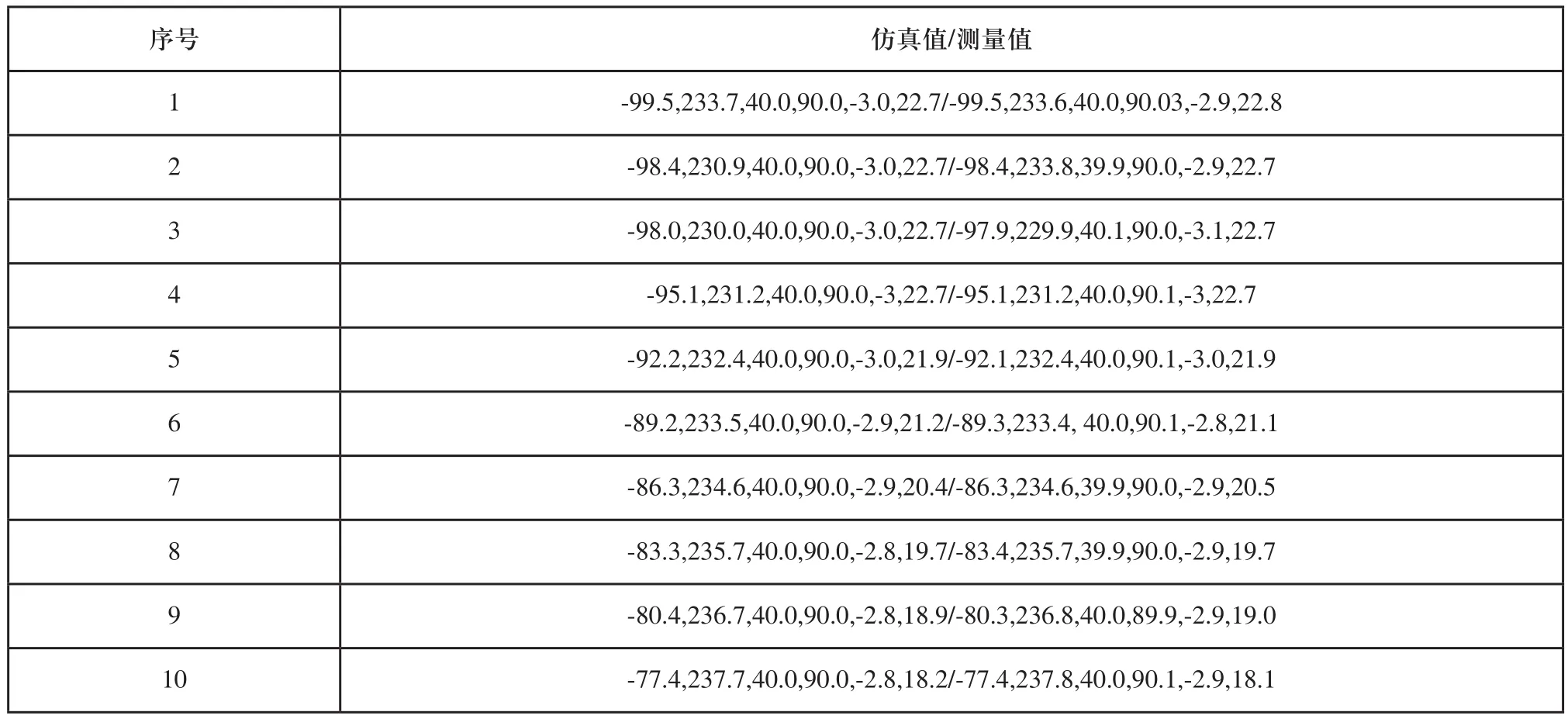
表2 传感器TCP相对工件位姿仿真值/测量值

4 测量实验

完成仿真后，利用仿真软件强大的后处理功能生成机器人测量程序，将其下载到真实的机器人中完成曲面测量，在测量过程中IGPS接收器时刻获得测量传感器TCP相对于工件的位姿。仿真值和测量值如表2所示（篇幅所限仅取10组），实际测量如图5所示，测量值与仿真值之间偏差如图6所示。

图6 曲面测量实验

通过对仿真值和测量值的分析可知，二者之间的位置偏差最大为0.1mm，角度偏差为0.1°，即实机器人的实际运行轨迹和被测表面法向相一致。

5 结论

以往的机器人测量系统基本上都是通过手眼标定来提高系统的精度，受各方面的影响因素较大，本文提出一种利用IGPS来实时获取工业机器人末端测量传感器在全局坐标系下的位置，通过轨迹规划技术保证测量轨迹时刻和被测工件表面法向相一致，为复杂零件的深孔形貌测量及基于全局位置的点云拼接奠定了基础。分析了测量机器人的运动学关系，通过仿真和实验验证了轨迹规划的正确性。

[1] 吕婧婧,黄明宇,吴修娟,等.基于三维模型的复杂曲面电磨底壳零件检测研究[J].制造业自动化,2010,04:83-85.

[2] 赵磊,赵新华,王收军,等.柔性测量臂的RPY建模与误差标定[J].光学精密工程,2016,02:365-371．

[3] 徐龙,王柱,刘爱明,等.基于激光扫描的逆向工程在检验检测中的应用[J].制造业自动化,2014,22:36-37,41.

[4] 王珏,伍立芬,邹永宁,等.Zernike矩边缘检测与多项式拟合的CT图像三维测量算法[J].仪器仪表学报,2012,02:442-449.

[5] 邓文君,叶景杨,张铁.面向机器人磨抛的激光点云获取及去噪算法[J].光学学报,2016,08:180-188.

[6] 李睿,曲兴华.工业机器人运动学参数标定误差不确定度研究[J].仪器仪表学报,2014,10:2192-2199.

Kinematics analysis and measurement path planning research of complex curved surface measurement robot

MA Guo-qing, LIU Li, ZHANG Ruo-yan, YU Zheng-lin, CAO Guo-hua

TP242

：A

1009-0134(2017)01-0080-05

2016-10-18

国家高技术研究发展计划（863计划）资助项目（2015AA7060112）；吉林省科技发展计划资助项目（201602040 16GX）；吉林省省级产业创新专项资金资助项目（2016C088）；长春理工大学青年科学基金（XQNJJ-2016-04）

马国庆（1988 -），男，吉林德惠人，讲师，博士研究生，研究方向为机器人形貌测量技术。