基于ANSYS的外啮合高压泵斜齿轮的接触应力及有限元模态分析

刘 坤，徐 雷，陈 沛

（四川大学 制造科学与工程学院，成都 610000）

基于ANSYS的外啮合高压泵斜齿轮的接触应力及有限元模态分析

刘 坤，徐 雷，陈 沛

（四川大学 制造科学与工程学院，成都 610000）

为避免齿轮因疲劳折断、齿面胶合等因素而引发生产事故，保证其具有良好的工作性能，因此有必要对高压泵斜齿轮进行静态及动力学分析。以高压泵斜齿轮为出发点，通过ANSYS对高压泵斜齿轮轮齿啮合处的受力情况进行静态分析，得到高压泵斜齿轮传动在载荷作用下的变形和应力，并校核其结构的可靠性，通过模态分析，获得高压泵斜齿轮的振动特性和固有频率，进而避免共振的发生。最后实验表明，通过静态分析求解的接触应力小于理论计算值，模态分析形象直观的反映出固有频率，不会发生共振，验证了结构的合理性，为准确分析齿轮工况提供了一种有效解决途径。

高压泵斜齿轮；ANSYS；接触应力；模态分析

0 引言

轮齿的弯曲强度是外啮合斜齿轮的重要的强度性能之一，而且齿根弯曲应力的大小直接影响着齿轮的使用寿命和生产安全。随着机械制造业的发展，外啮合斜齿轮高压泵在液压系统中扮演着重要角色，在实际工作情况下，轮齿由于受载荷的作用易发生疲劳破坏，为避免齿轮的疲劳破坏，保证其良好的工作性能，因此，有必要对轮齿所受到的应力进行分析。

朱如鹏[1]等利用有限元分析对齿轮接触应力和模态等特性进行了研究。Tsuta[2]分析了齿轮轴的刚度特性对外啮合斜齿轮传动性能的影响，分析了齿轮啮合过程中接触应力的变化。胥国祥[3]对面齿轮进行了动力学分析，分析了齿轮啮合过程中接触应力的变化。刘刚田等[4]借助于Pro/Engineer生成弧齿锥齿轮模型，利用ANSYS有限元分析，分别计算了接触应力和弯曲应力。可知，有限元分析在齿轮的静态分析、动力学分析等方面得到了广泛的应用。通过对齿轮泵轮齿啮和过程进行静态分析和模态分析，可以比较精确地提供齿轮泵齿轮工作过程中的运动情况，从而获得齿轮的应力分布和振动特性。

本文首先根据GPD2型外啮合高压泵斜齿轮的设计参数，通过SolidWorks 14.0完成其建模并进行装配，将模型数据变换后导入ANSYS软件，综合考虑了摩擦接触，扭矩和转速变化等因素，得到了在多齿対接触情况下，齿根处弯曲应力场的分布及其变化规律。

1 斜齿轮有限元模型的建立

本文以四川长江液压件有限责任公司的GPD2型高压泵外啮合斜齿轮为研究对象，齿轮泵主要技术参数如表1，外啮合斜齿轮的齿面是渐开线螺旋面，齿轮副几何参数如表2所示。依据设计参数，在SolidWorks 14.0中进行建模并装配，得到外啮合高压泵斜齿轮的组成如图1所示。使用ANSYS 15.0对轮齿的接触啮合进行分析。

在本文的计算中，在齿宽方向划分了50层单元，在齿高方向划分了6层单元，轮齿采用六面体单元划分，齿轮副模型共有为120232个单元，205188个节点。网格划分原则依据遵循齿面接触区域细化，其余区域较稀疏。

齿轮啮合属于接触非线性问题，既有由摩擦产生的非线性，也有由接触压力变化、接触面积产生的非线性[5]，它是一个反复迭代的过程，考虑到齿轮轴对接触分析结果的影响较小，同时为了简化计算，因此对齿轮的结构进行适当简化，本文取斜齿轮的轮齿部分进行啮合分析，得到齿轮副网格划分结果如图2所示。

表1 斜齿轮主要技术参数

表2 齿轮副几何参数

图1 高压泵齿轮啮合图

图2 齿轮副网格划分图

2 接触对的建立与模型的加载

分别对斜齿轮进行静态分析和模态分析，通过静态分析，确保外啮合高压泵斜齿轮承受稳定载荷的状态，来确定斜齿轮在稳定载荷作用下结构的可靠性；通过模态分析，来确定高压斜齿轮泵结构振动的固有特性，即固有频率和振型。

2.1 创建接触对

重合度是衡量齿轮啮合的重要指标，斜齿轮齿条重合度包含向重合度和端面重合度，计算公式为：

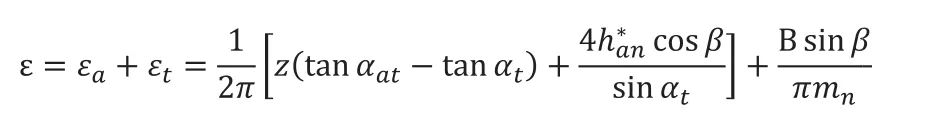
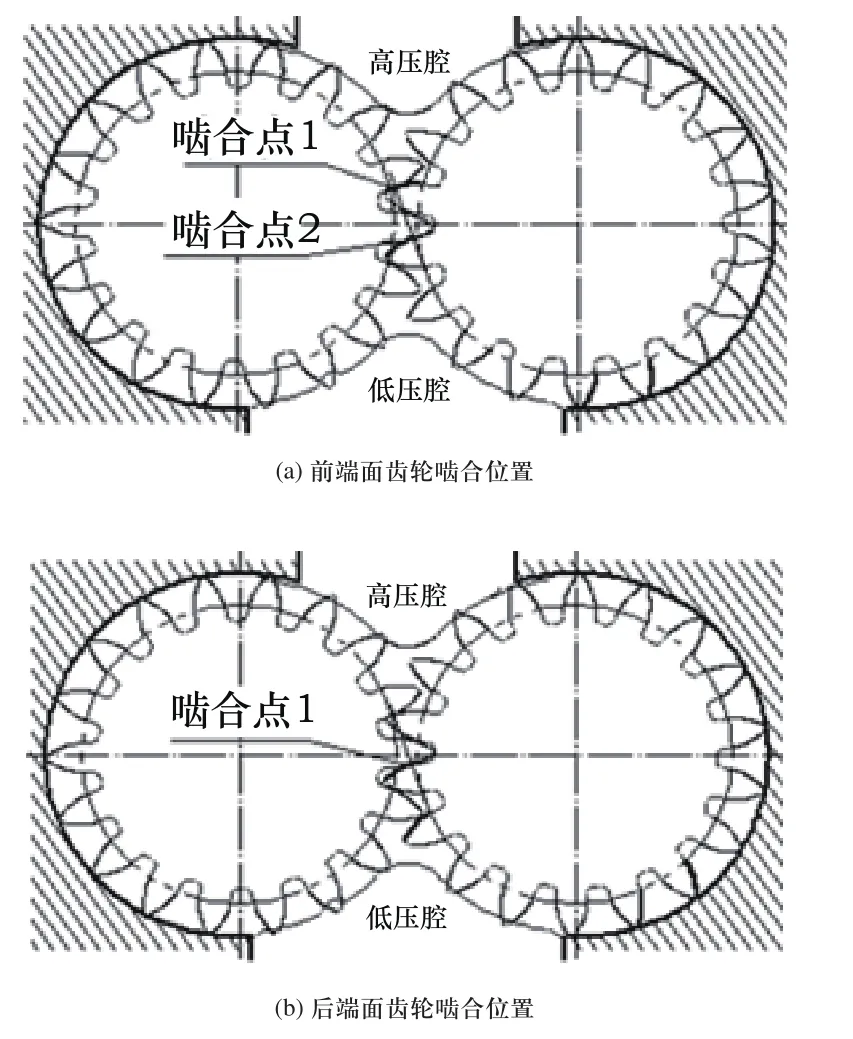
图3 齿轮啮合位置图

2.2 外啮合高压泵斜齿轮静态分析

在SolidWorks 14.0中进行装配，然后将装配好的齿轮泵齿轮模型导入ANSYS软件后，设置主动齿轮和从动齿轮的材料为结构钢，泊松比为µ=0.3，弹性模量E=2.5×105Mpa，密度为7.85×10-6kg/mm3，接触面的类型选为“Frictional”，摩擦系数设置为0.05。

高压泵正常工作时，主动轮靠外界电动机输入转矩来带动从动轮，实现齿轮的啮合运动，此时，从动轮受阻力矩。在静态力学分析中，假设主、从动齿轮接触的瞬间，从动轮不动，对从动轮内圈进行固定约束，主动轮施加转速为2000r/min。

对轮齿啮合接触进行求解分析，可得到其等效应力分布图，安全系数。进而确定最大应力和最小安全系数，求解结果分别如图4～图6所示。

图4 等效应力分布图

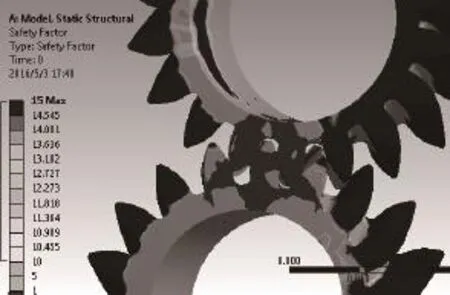
图5 安全系数分布图

图6 等效应变分布图

在齿轮啮合过程中，齿根受到的弯曲应力也会不断变化，在轮齿啮合区域应力较为集中，齿轮接触应力校核公式[6]为：

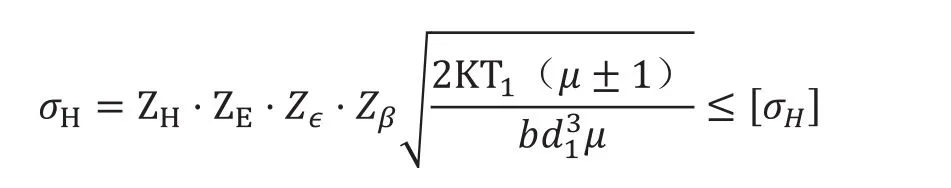
式中：ZH为节点区域系数；ZE为弹性系数；θd为齿宽系数；K为载荷系数；Z为重合度系数；Zβ为螺旋角系数；T1为转矩，单位为N·mm；d1为从动齿轮节圆直径，单位为mm；μ为齿轮齿数比。

通过理论计算的齿轮接触应力为915.8Mpa。

由图4可知，最大等效应力为984.01Mpa。将ANSYS分析结果与理论计算值进行对比，两者比较相符。图6为等效应变分布图，从变形情况看，可知弹性应变的分布情况为：应力沿齿轮轴向向齿轮啮合的区域由小变大。

由图5可知，齿轮最小安全系数区域在主动轮轴肩处，最小系数为1，说明其最易受到破坏，而其他区域的安全系数大于1。若最小安全系数大于1，则表明齿轮轮齿接触部分疲劳强度符合设计要求。

2.3 外啮合高压泵斜齿轮模态分析

通过模态分析，可使斜齿轮结构设计避免共振的发生，可以用来确定振动特性、固有频率的，让我们认识到结构对不同类型的动载荷是如何响应的，从而了解高压泵斜齿轮的动力学性能[7]。

在对斜齿轮进行模态分析时，其材料属性、网格划分与静态分析相同，主要分析斜齿轮在自由模态下的固有频率和振动特性，不考虑预应力的影响，不对齿轮模型施加载荷，约束两个斜齿轮内圈节点的自由度，模型在导入ANSYS软件时，已经自动检测并创建接触对，将接触类型设置为“Frictional”。

采用迭代求解器进行求解，提取前10阶模态。表3为高压泵斜齿轮前10阶的固有频率。

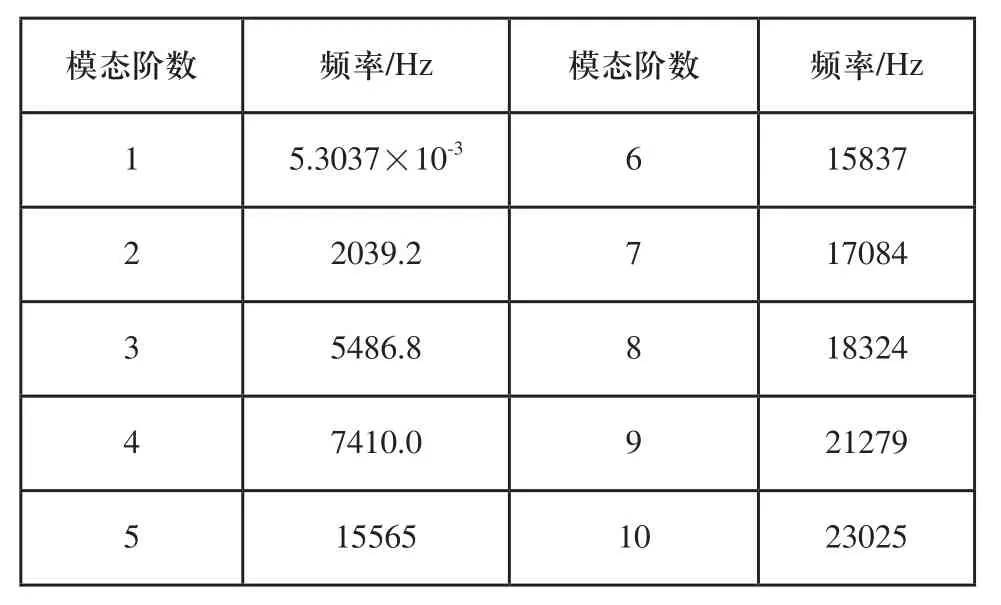
表3 高压泵斜齿轮前10阶固有频率

【】【】

The contact stress and finite element modal analysis of high pressure pump helical gear based on ANSYS

LIU Kun, XU Lei, CHEN Pei

TH3

：A

1009-0134(2017)01-0004-05

2016-09-01

川大-泸州高校科研基金项目（2014CDLZ-G23-SCU，2015CDLZ-G19-SCU）

刘坤（1991 -），男，山东人，硕士研究生，研究方向为计算机辅助设计。