基于正交试验的S管道参数优化设计

宫百香，冉杰娃，韩 冬，王志强

（长春工业大学 机电工程学院，长春 130012）

基于正交试验的S管道参数优化设计

宫百香，冉杰娃，韩 冬，王志强

（长春工业大学 机电工程学院，长春 130012）

在泵送混凝土过程中，换向阀中的S管道常出现堵塞现象。为防止混凝土堵塞S管道，采用Fluent软件建立S管道仿真数值模型，并结合正交试验表在给定条件下对模型进行多次数值模拟，得到S管道各参数的最佳值。将优化前后数值模拟结果进行对比分析，分析表明，优化后S管道混凝土流动更流畅。

S管道；数值模拟；正交试验；参数优化

0 引言

换向阀作为混凝土输送泵中的关键部件，在混凝土泵送过程中通过换向，使换向阀中的S管道与两个混凝土输送缸交替连接，实现混凝土的排料和吸料动作，在泵送过程中起到中间桥梁的作用[1]。S管道由于其形状和安装的特殊性，S管道内混凝土流动压力损失较大，容易引起混凝土堵塞S管道[2,3]。轻微的堵塞会影响泵送工作进程，严重的堵塞可能会发生爆管等危及人生安全的事故，故在泵送过程中应尽可能避免S管道的堵塞。

S管道中混凝土运动情况比较复杂，S管道结构参数的改变对混凝土的流动压力影响较大。S管道压力损失大小可反映混凝土流动特性。压力损失越小，混凝土流动越流畅，混凝土堵塞S管道的可能性就越小[4]。

针对S管道堵塞问题，首先研究S管道压力损失与其结构参数的关系，并采用正交试验设计和FLUENT数值模拟方法对S管道进行优化设计。

S管优化设计的原则是，减少混凝土在S管道内的流动阻力，促进混凝土流动顺畅，防止混凝土堵塞S管道。

1 S管道压力损失计算

1）S管道几何参数计算

由图1可知，S管主要由AB、CE两段抛物线弯管和中间BC段直管道组成[5]。由BE直线和AB、CE两段抛物线相切可得其几何角度关系：

图1 2S管道的结构示意图

由几何关系可得：

由式(1)、式(2)可得：

2）S管道BC直管段的压力损失计算

混凝土流体可视为充满整个管道的“柱塞流”[6]。如图2所示的BC段，对BC段进行微元处理，微元长度为dx，研究直管段的压力损失。

在泵送过程中，主要存在的力有混凝土“柱塞流”与管壁间的摩擦力、混凝土流动不稳定时产生的惯性力、混凝土在水平方向的重力分离。混凝土受力平衡公式：

式中：D为直管段BC的直径（mm）；θ为BC段与水平面的夹角（°）；V为混凝土的流动速度（mm/s）；ΔP为BC段的压力损失（Pa）；γ为混凝土容重（g/mm3）；为混凝土的密度（g/mm3）；K1为粘着系数（Pa），K1=(3.0-0.1S)×102；K2为速度系数（Pa/mm/s），K2=(4.0-0.1S)×102；S为混凝土的坍落度。

将x关于压强P进行微积分得：

图2 受力模型

3）AB段抛物线弯管的压力损失计算

如图2所示AB段，AB段抛物线长度较短，可近似看作是圆弧，混凝土在S管道弯曲部位的压力损失和在直管段的压力损失相似，混凝土在弯曲部位的受力平衡公式：

式中：ΔP0为弯曲部位的压力损失（Pa）；α为弯曲部位的弯曲角度（°）；R为弯曲部位曲率半径（mm）。

S管道CE段弯管的压力损失为μΔP0（0＜μ＜1）。

S管道总的压力损失近似等于直管的压力损失和弯曲部位的压力损失之和：

由式(2)、式(3)、式(6)、式(7)得：

由式(8)可知，影响S管道压力损失的因素有S管道的直径、曲率半径、水平长度L1、L2、L3。故需对这些参数进行优化设计来减小压力损失，促进混凝土顺畅流动，防止混凝土堵塞S管道。

2 S管道正交试验设计

正交实试设计采用数理统计和正交性原理，从大量试验点中选取适量具有代表性的试验点，用正交表进行合理安排试验的方法，其试验结果重复性好、试验次数少，分析简便而得到广范应用[7]。影响混凝土堵塞S管道的因素较多，在进行试验时，试验量比较大，符合正交试验的特点，因此采用正交试验对各因素进行优化设计。

1）S管道初次正交试验设计

将压力损失作为试验指标，S管道的曲率半径、直径和各段的水平长度作为试验因素，并套用正交试验表L16(45)，进行正交分析[7,8]。各影响因素的相关参数的选取，参照国内生产厂家（如三一重工）的技术参数进行适当取舍，如表1所示。

表1 参数优化水平-因素表（mm）

采用FLUENT软件进行初次数值模拟，将压力损失（Pa）作为试验结果[9]，得正交实验结果如表2所示。通过极差分析可知，因素和水平数完全一致时，S管道直径的极差值最大，对混凝土的压力损失影响较大。S管道的直径和曲率半径R之间的交互作用（联合作用）的极差值最小，即对压力损失影响较小，可以忽略。

表2 参数初次优化结果列表

从单因素指标考虑，如图3所示，S管道直径和曲率半径增大时，S管道中混凝土流体的压力损失均减小。因此，增大S管道直径和曲率半径，均可改善混凝土的流动特性。在选用S管道时，根据泵送量，应尽量取较大值为宜。

图3 因素指标效应曲线图

2）S管道二次正交试验设计

S管道总长L为定值，S管道各段水平长度L1、L2、L3（如图1所示）的合理分配对S管道中混凝土的顺畅流动有重要影响。因此设计了如表3所示的水平-因素表，并采用L16(45)正交表进行正交试验[7,8]。

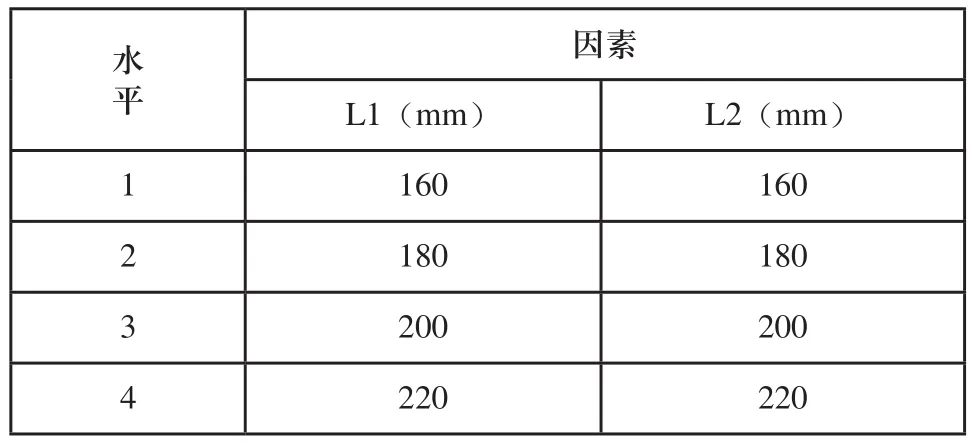
表3 S管道水平长度水平-因素表

如表4所示，经过极差分析可知，S管道BC段水平长度L2的极差值最大，即对试验结果影响最大，需优先确定L2的值。当L2的值为200mm时，S管道中混凝土的压力损失较小，表明S管道中混凝土的流动特性较好。此时，L2的值是S管道总长L值的三分之一，符合单因素优选法中平分法的选择原则，故取L2的值为200mm。

表4 参数优化结果

在L2段最佳长度确定的情况下，取L1段的长度从180mm～250mm均匀增加，进行8组数值模拟。

如图4所示，压力损失曲线L1的长度在225mm附近有极小值，即为最优值。当L1取值225mm时，L3为175 mm。此时S管道各段的水平长度比例为定值，与当前大多数生产S管道的企业（如三一重工）所采用的经验比例1.4:1.2:1接近。

图4 L1段抛物线长度与压力损失关系图

3）S管道结构最佳参数确定

通过对S管道的结构参数的优化设计，得S管道各参数的最佳值，如表5所示。

表5 S管道结构参数优化结果

3 S管道优化结果分析

优化前后S管道的压力云图如图5、图6所示，优化后S管道整体压力损失明显减小，S管道弯曲部位内外侧的压力差减小幅度较大，相当于减少弯曲部位离心力，防止由于高压部位的流体沿管壁向低压部位挤压使流体出现“回流”的现象[8,10]。

图5 原始压力分布云图

图6 优化后压力分布云图

优化前后S管道的速度云图如图7、图8所示，在弯曲部位，优化前S管道内侧流速明显大于外侧，使混凝土在弯曲部位形成涡流[10]，容易引起混凝土在弯曲部位产生集聚；优化后弯曲部位内外侧的速度差明显减小，且整体速度差也明显减小，说明混凝土流动流畅。

混凝土流体由于固-液间的耦合作用，使S管道中间流体运动速度大，壁面周围的运动速度小，符合“Bingham”流体特点[6]。

图7 原始流速云图

图8 优化后流速云图

4 结论

分析影响S管道压力损失的主要结构参数，并进行优化，得以下主要结论：

1）S管道压力损失的主要影响因素，S管道直径、曲率半径和S管道各段的水平长度。

2）S管道内压力损失随管道直径和曲率半径的增大而减小，应选择较大的管道直径和曲率半径；S管道各段合理的水平长度，可使混凝土顺畅流动。

3）优化后S管道流体的压力差和速度差明显降低，流场分布更均匀，保证混凝土流动更加顺畅，降低混凝土堵塞S管道的可能性。

[1] 张国忠.现代混凝土泵车及施工应用技术[M].北京:中国建材工业出版社,2004.

[2] 贾向春,罗朝廷,郑朝保.风送型湿喷机管道输送系统进风分配阀结构对流场影响的分析研究[J].铁道建筑,2011(4):149-151.

[3] David C W.Turbulence Modeling for CFD[M].California,DSW Industries Inc,1994.

[4] 厉秀珍,游小平,李自光.HBTS60砼泵S管动力学分析及优化[J].公路与汽运,2013(1):146-149.

[5] 许在坤,于洪恩.混凝土泵水平管阀设计[J].工程机械,1997,28(1):9-10.

[6] 黄明奎.公路材料流变学[M].成都:西南交通大学出版社，2010,6.

[7] 何为,薛卫东,唐斌,等.优化实验设计方法及数据分析[M].北京,化学工业出版社,2012.2.

[8] 张尧武,曾卫东,戴毅,赵永庆,周义刚,王凯旋.基于虚拟正交试验的热推弯管工艺参数优化设计[J].塑性工程学报,2009,16(6):92-97.

[9] 吴占松,谢菲.用于管道煤粉流量测量的文丘里管型设计及优化[J].清华大学学报(自然科学版),2007,47(5):666-669.

[10] 王永成.基于CFD的Z形弯管流场模拟分析及其结构优化[J].液压气动与密封,2014,34(9):29-32.

图7 高压泵斜齿轮各阶模态变形

由图7可知，第5阶和第7阶振型对应的相对位移较大，分别为2.9343mm和2.9168mm，且斜齿轮的模态变形主要表现为扭转振和径向振。通过模态分析，得到齿轮传动系统的固有频率，可知固有频率与激振频率不相同，避免了共振的发生。其中第2、8和10阶的相对位移比较大，表现为扭转振，表明扭转振对高压泵斜齿轮传动性能的影响比较大，在传动中应该尽量避免此类振型的影响。

通过对齿轮轮齿啮合进行模态分析，可进一步分析轮齿啮和过程中，啮合位置的自振周期和变形情况，从而可以帮助分析人员估算其他动力学分析参数，确定合理的瞬态分析时间。

3 结论

1）利用SolidWorks14.0对外啮合高压泵斜齿轮进行三维建模并完成装配，仿真分析中考虑了齿面之间的摩擦接触，转速变化、扭矩等因素，较好地模拟了轮齿接触面应力场的变化特性。

2）齿面接触区域的应力内侧较低，外侧较高， 齿根区域外侧应力要低于内侧，扭转振对高压泵斜齿轮传动性能的影响比较大。

3）结合静态分析与模态分析，能有效地对齿轮轮齿啮合进行模拟仿真，仿真结果与实际结果比较符合，为外啮合高压泵斜齿轮应力分析、强度校核、结构振动特性分析和优化设计提供了快速有效的方法。

参考文献：

[1] 朱如鹏,曾英.正交面齿轮弯曲应力的分析[J].机械科学与技术(西安),2001,20(5):708-709.

[2] 胥国祥,张以都.基于LS-DYNA的正交面齿轮动态接触分析[J].装备制造技术,2010,24(2):56-59.

[3] Tsuta T,Yamaji S.Finite element analysis of contact problem. Theory and Practice in Finite Element Structure Analysis[M]. Japan:University of Tokyo Press,1973.

[4] 刘刚田,赵萍,杨耀山,等.弧齿锥齿轮的实体造型和有限元强度分析[J].矿山机械,2003,10:61-62.

[5] 杨晓宇.齿轮传动系统动力学特性的有限元分析及试验方法研究[D].吉林:中国科学院长春光学精密机械及物理研究所,2005.

[6] 邱宣怀.机械设计[M].北京:高等教育出版社,2011.

[7] 许进峰.Ansys workbench 完全自学一本通[M].北京:电子工业出版社,2014,9.

Optimal design of parameters for S pipe-bending based on orthogonal experiment

GONG Bai-xiang, RAN Jie-wa, HAN Dong, WANG Zhi-qiang

TU64

：A

1009-0134(2017)01-0008-04

2016-09-14

液压活塞式混凝土输送泵防堵系统研究（吉教科合字【2015】89号）

宫百香（1965 -），女，吉林农安人，副教授，硕士，研究方向为机械CAD/CAM。