尝试运用v—t图像破解运动学问题

陈文月

中图分类号：G720 文献标识码：A 文章编号：1002-7661（2017）03-0002-03

在高中物理学习阶段，面对茫茫“题海”中千“题”百怪、令人茫然不知所措的难题，不少人也许会产生顿挫之感。仅就运动学模块而言，这类问题也随处可见。不过，一旦熟练掌握并能够巧用v-t图像，其中的一些问题将会柳暗花明、迎刃而解，似乎算不上什么难题。

一、用v-t图像求解最大速度

例1. 一辆从车站始发的汽车，做匀加速运动，走了12s时，司机发现还有乘客没上来，于是立即做匀减速运动至停车，总共历时20s，行进了50m，求：（1）汽车的最大速度是多少？（2）开始减速前，该车已经走过了多少路程？

此题只告诉了匀加速、匀减速的时间及最大的位移，但并没有告知加速度的具体情况，显然不能用Vt=Vo+at来简单求证。但是，既然提供了“由车站始发”“匀加速”“匀减速”及最终“停车” 的“时间”“位移”等条件，我们就可以通过v-t图像来加以解决，即：该汽车从“0”速度开始，在匀加速至12s时，达到其最大速度（Vm），然后作匀减速运动，至第20s时，其速度减至最低速度（0），而其速度变化图像与t轴围成的三角形面积（S），则是该车行进的距离（X），该三角形的顶点（h）即为该车的最大速度（Vm）。据此，绘出v-t图如下：

这样，就用简洁、明了的方式求得：该汽车的最大速度达到每秒5米，减速之时已经行驶了30米。

二、通过v-t图像比较时间长短

例2. 如图2所示，ABC和DE是两个高度相等的光滑斜面，ABC由倾角不同的两部分组成，且AB+BC=DE，两个相同的小球a、b分别从A点和D点沿两斜面由静止同时滑下，不计转折处的能量损失，则滑到底部的先后次序是（ ）。

A.a球先到 B.b球先到

C.两球同时到达 D.无法判断

判断此题，切不可凭感觉用事。从题中所给的条件可知，两球质量相等，所处高度也相等，由此可直接得出的第一个推论是：两球的重力势能相等。而既然两球的重力势能相等，那么，按照机械能守恒定律，两球在滑到底部时，所做功相等，各自的动能也相等。于两球质量相同，所以，可以得到的第二个推论是：两球在滑动到底部时的末速度（Vt）也就相等。另外，既然AB+BC=DE，所以，两球在下滑过程中的位移相同。当然，两球都是从静止状态释放的，所以，各自的初速度均为Vo=0。明确了以上几点，就可以画出两球运动的如下v-t图像：

此v-t图像根据题意（大致）表明，一开始（即AB段时），a球的加速度（即直线斜率）大于b，但到后来（即BC段时），其加速度（直线斜率）小于b；同时，既然根据题意，AB+BC=DE，那么，图像oat1所围的面积要和obt2所围的面积相等。从满足这两个条件的v-t图像中不难直观看出，a球下降所用的时间（t1）必然要比b球所用的时间（t2）短，故，答案为A，a球先到。

三、运用v-t图像判断运动方式

例3.由甲地从静止出发，沿平直公路驶向乙地的一辆汽车，先以加速度a1做匀加速运动，最后以加速度a2做匀减速运动，中间可能有一段匀速运动过程，也可能没有匀速运动过程，到乙地恰好停下。已知甲、乙两地相距为s。试问：要使汽车从甲地到乙地所用的时间最短，汽车应做怎样的运动？

此题提供的信息要点有二：1.不论汽车采用什么样的运动方式，甲乙两地的距离是个定值，即汽车的位移为S；2.汽车的初速度和末速度均为0，而且不论采用什么运动方式，其最初和最后两段距离的运动方式均有加速度，只不过最初为匀加速（a1），最后为匀减速（a2），两者也不变。因此，可以直接按照满足此条件的如下v-t图像对各种运动方式进行比较，看哪一种运动方式所用时间最短。时间最短者即为应当采用的运动方式。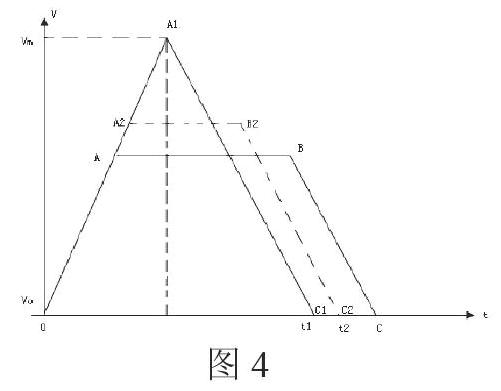

如图4所示，设OABC所围成的图像表示甲乙两地的距离S，根据题意，不论是采用先加速接着马上减速的运动方式（如OA1线段与A1C1线段所示运动轨迹），还是先加速，然后匀速，接着再减速的运动方式（如OA2、A2B2与B2C2线段所示运动轨迹），△OA1C1的面积、梯形OA2B2C2 的面积，必须与梯形OABC的面积相等，而且，既然各种运动方式最初的加速度（a1）和最后的加速度（a2）均保持不变，这就意味着A1C1线段、B2C2线段均与BC线段保持平衡（斜率不变）。由此可以直观的看出，采用“先加速接着马上减速”的运动方式所用时间（t1）比先“加速然后匀速接着再减速”的运动方式所用时间（t2）要短，应当采用前者。

四、借助v-t图像计算上升高度

例4. 一质量为m = 40kg的小孩在电梯内的体重计上，电梯从t=0时刻由静止开始上升，在0到6s内，体重计示数F的变化如图5所示。

试问：在这段时间内电梯上升的高度是多少？取重力加速度g=10m/s2。

解答此题，首先应当明确的是，小孩的重力mg=400=400N；当其乘坐电梯上升时，如果电梯的上升是匀速的，体重计的示数就保持不变，应为400N。但当电梯加速时，由于超重，体重计的示数会显示高于400N，相反，当减速时，体重计的示数则会显示低于400N，而且，只要是进行匀加速或匀减速，该增加或减少的数值也会保持恒定。据此观察体重计示数F的变化图可知，第一，在最初的2s内，电梯是由静止开始进行匀加速上升的（示数计读数高于400N而且恒定）；第二，在随后的第2至第5s内，电梯是匀速上升的（示数读数等于400N）；第三，在最后1s内（第6秒内），电梯开始进行匀减速（上升）直到停止（即电梯上升的最高点）。

问题是，电梯及小孩上升的加速度（a1）、匀速上升的速度（vt）以及匀减速时的加速度（a2）究竟是多少呢？

根据牛顿第二定律，F合=ma1，即，440-400=401，由此得知，电梯匀加速上升的加速度a1=1m/s2。同理，电梯匀减速上升时，320-400=40€譨2，故，匀减速上升时的加速度a2= -2m/s2。根据Vt=Vo+at可知，在电梯上升的第2至第5s内，其匀速上升的速度（即第2s末的速度）Vt=0+（1）=2m/s。

将上述结论转换为电梯及小孩的v-t运动图像，则有下图6：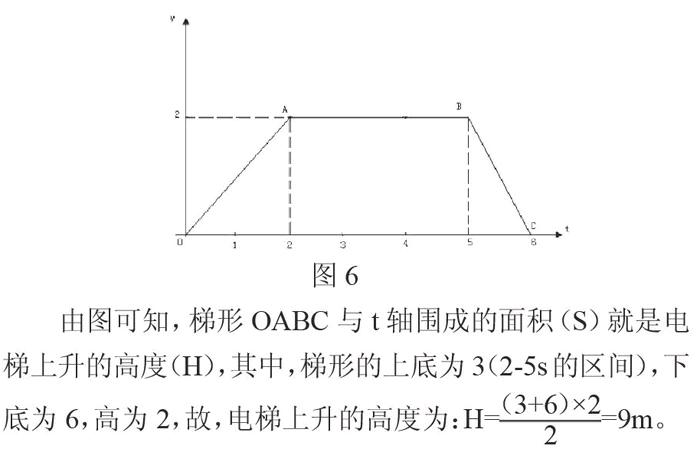

五、小结

综上可见，用v-t图像求解运动学模块的有关问题，有时可以简化解题的过程，化繁为简，具有直观、形象、简明的特点。其实质是把复杂的物理量之间的代数关系转化为几何关系，核心是通过速度图线与时间t轴围成的面积来加以比较、计算或分析。因此，运用这一方法，首先应当认真审题，切不可遗漏条件。除了要注意把握题目明确给定的条件（如时间、质量、位移、长度，初速度、末速度状态）外，还要仔细发掘题目中隐含的问题。比如，例4中的加速度a1、a2及匀速上升的速度，例2中a、b两球的末速度等。其次，在将物理量转化为V-t图像时，必须时刻牢记，该图像围成的几何面积实际上表示的只是运动学上的位移或者距离，必须对几何学中的基本公式、定理（如三角形的面积、梯形的面积公式计算等）熟烂于胸。再次，在v-t图转化中，尤其要注意速度线段的曲与直、倾斜度、等高线、起始点。只有匀速或匀加速运动才能转化为直线，只有在具有加速度的运动中，该直线才有斜率，而且加速度越大，斜率越大。而v-t图像中的等高线，则意味着速度相等，当然，速度线段与t轴相交的地方，也意味着速度相等（0）。最后，v-t图像的运用和物理学的相关内容紧密相关，如果物理学的基础不扎实，就势必严重影响到v-t图像法在运动学问题上的科学运用。比如，如果对动能定理、机械能守恒定理认识模糊，就不可能对例2问题进行v-t图的准确转化；如果对牛顿第二定律没有真正领会，就不可能对例4问题的加速度用精准的斜线进行表示。