基于贪心策略的大规模MIMO系统信号检测算法

陈发堂，易 润，黄 菲

(重庆邮电大学 移动通信重庆市重点实验室，重庆 400065)

基于贪心策略的大规模MIMO系统信号检测算法

陈发堂，易 润，黄 菲

(重庆邮电大学 移动通信重庆市重点实验室，重庆 400065)

针对传统球形译码性能和计算复杂度受到初始半径及搜索策略制约的问题，提出了一种新的基于M算法的贪心策略球形译码检测算法，对树搜索的方法进行了改进，先将该层信号集合中的距离增量进行排序，然后选择距离增量最小的M个点为信号点，这样每一次选取的信号点相对该层都是局部最优的。仿真结果表明，相比于传统球形译码检测算法，当M为1时，该算法可以降低约30%的计算复杂度。使球形译码算法的效率得到了很大的提高，可以运用于大规模MIMO系统中。

信号检测；球形译码；贪心策略；M算法

4G网络是当前各地无线通信系统的主流网络，信号检测算法的性能和算法复杂度是整个无线通信系统的关键部分。然而，大规模MIMO的引入带来系统容量和频谱利用率大幅度增加的同时也给接收端检测技术带来更大的挑战，信号检测的算法复杂度呈指数级增长。这使得接收端准确恢复出发送端天线的信号面临一个大的难题。因此，研究性能较好且算法复杂度适中的信号检测算法是整个系统的关键。

目前已经提出了很多信号检测算法，其中ML(最大似然)算法是检测性能最优的算法，其本质是遍历了所有可能发送信号符号的星座点，以距离接收信号最近的星座点作为发送信号，但算法复杂度太高。于是各种降低复杂度并保证性能不过分损失的信号检测算法被提出。如ZF(迫零)算法、最小化均方误差算法(MMSE)、QR分解算法等。

球形译码(SD)算法在性能和复杂度方面取得了很好的折中，它是一种能得到最大似然检测性能的低复杂度检测算法，通过设定一个以接收向量为中心的超球，仅搜索超球内的格点来找到最大似然解。球形译码算法的性能依赖于初始半径的选择，初始半径选择太大会导致树搜索时有太多不必要的搜索点，导致时间复杂度的提高。初始半径太小可能会导致在给定的多维球体内没有解，导致性能的大幅度降低。所以要降低球形译码算法的复杂度和提高译码性能必须准确地设置搜索半径。

文献[1]提出的基于阈值的球形译码能够有效降低复杂度，但对获取半径过程受到阈值的影响，其在低信噪比的情况采用MMSE方法获取；文献[2]给出了一种低复杂度球形译码，该算法采用固定阈值作为可靠性判断标准，将ZF算法与球型译码算法相结合，但ZF算法性能较低；文献[3]提出的蚁群球形译码有效降低了算法复杂度，但涉及到迭代和概率问题，实现过程繁琐，不适用于大规模MIMO系统。文献[4]提出了一种贪心搜索的策略求解TSP问题；文献[5]提出了一种基于黄金分割的搜索半径球形译码，减少了搜索格点；文献[6-10]提出了对球形译码初始半径和搜索树进行改善来降低算法复杂度，但是都受到初始半径的约束。针对球形译码存在的缺点，本文提出了一种基于M算法的贪心策略球形译码(SDBGS-M)算法。该算法是在球形译码检测算法的基础上改进树搜索的方法而得到的。

该算法不需设置初始搜索半径，不再像传统球形译码算法那样按照星座图从左向右依次搜索，而是先将该层信号集合中的距离增量进行排序，然后选择距离增量最小的M个点为信号点，这样每一次选取的信号点相对该层都是局部最优的。从而大幅度降低了搜索复杂度，使球形译码算法的效率得到了明显提高，能够完全适用于大规模MIMO中。

1 系统模型

MIMO系统由图1所示，发射端有M根天线，接收端有N根天线。编码后的比特流映射到M维的传输符号矢量X∈OM，O表示发送信号星座点向量空间。

图1 M×N的MIMO系统原理图

经过平坦瑞利衰落的高斯白噪声信道后，MIMO系统接收端信号可表示为

y=Hx+n

(1)

式(1)采用复数信号模型。其中，y=[y1,y2,…,yN]T是接收天线端的信号向量，x=[x1,x2,…,xM]T是发射天线端的发射信号，H为M×N的信道传输矩阵且满足高斯分布；n为各项独立同分布且均值为零、方差为σ2的高斯分布。

ML作为MIMO系统的最优检测算法，就是使n达到最小。而ML本质上是在发送信号星座点矢量空间中寻找距离接收信号矢量最近的格点的问题，也就相当于整数域的最小二乘问题，即

(2)

2 球形译码

球形算法的基本思想是：首先计算出球形译码的初始搜索半径ρ0，然后以接收信号矢量为球心，以ρ0为半径的球体内进行搜索格点，记录下搜索路径的同时根据每一维信号栅格点中格点的距离增量更新搜索半径ρ，循环往复，直到半径ρ内没有符号可以搜索，最后一次记录的搜索路径即为所求。

球形译码算法搜索前需先计算出初始搜索半径ρ0，其半径定义为

(3)

式中：n为接收信号的维数；σ2为高斯白噪声方差；α为初始化半径系数。

在球形译码算法中，把接收信号向量空间看作以y为中心的球，即

(4)

对H进行QR分解，可得

(5)

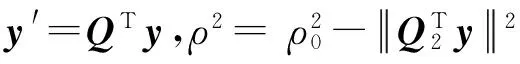
式(5)变为

(6)

将式(6)展开，可得

(7)

定义部分欧氏距离为

(8)

假设当前搜索的是第1层，则欧氏距离为

(9)

相邻节点之间的部分欧氏距离之间的关系为

(10)

MIMO信号检测问题可以看作是一个具有K层的树，搜索所有叶子节点找出根节点和叶子节点之间最小的的欧氏距离[6]。

图2是QPSK调制下球形译码的搜索树。

图2 QPSK调制下的球形译码算法的搜索树

搜索时，从D=K层开始搜索，逐层向下搜索直到D=1，此时的部分欧氏距离如果小于初始半径ρ0，则保存该条搜索路径及根节点到该叶子节点的欧氏距离，并用此值替换初始半径ρ0并重新开始搜索；算法采用的是深度优先搜索方式进行，按照信号的星座点顺序，从左向右依次枚举所有的星座点。显然在这种方式下，半径ρ收敛得很慢。

鉴于球形译码算法的缺点，本文提出一种基于贪心策略球形译码(SDBGS-M)算法，它对初始半径不敏感，同时还能够让半径ρ收敛更快，进一步减少搜索的信号点数，从而快速找到最优解。

3 基于贪心策略的球形译码检测算法

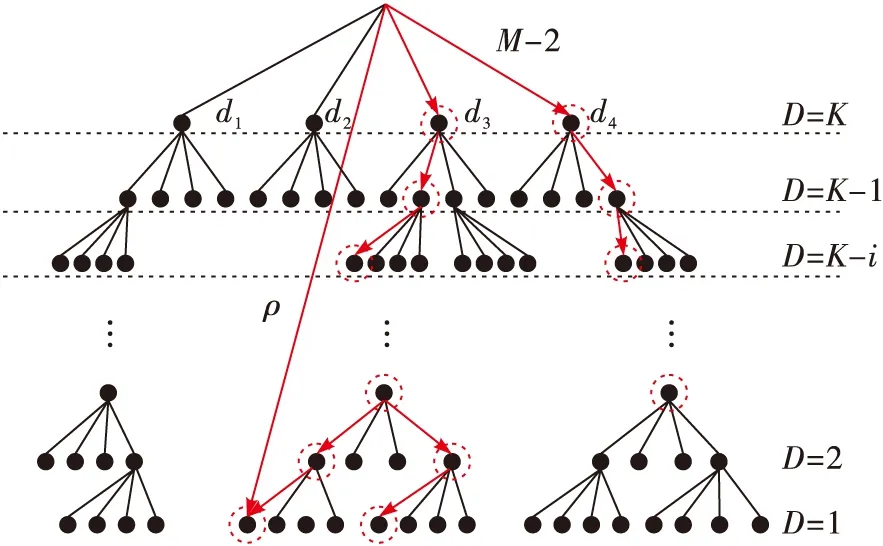
贪心策略是指所求问题的整体最优解可以通过一系列局部最优的选择而得到。贪心算法通常以自顶向下的方式进行，每作一次贪心选择就将所求问题简化为规模更小的问题。SDBGS算法遵循深度优先搜索的原则，但是在搜索过程中，不再按照星座图从左向右依次搜索，而是选择该层信号集合中距离增量最小的信号点，这样每一次选取的信号点，相对该层都是局部最优的[11]。例如在搜索第D层信号时，首先计算之前第D+1层的信号XD+1相对于该层的星座点XD的距离增量值T(y(XKD + 1)D,RD,DXD)，然后按照从小到大的顺序将其排序，选择其中距离增量最小的M个信号点继续向下搜索。详细说明如下：

假设当前搜索的是第一层，则欧氏距离表示为

(11)

T(·)用来表示距离增量，把式(11)写成分段式如下

(12)

从第K维开始，根据式(8)计算YK与XK之间的距离增量为

T(yK,RK,KX1),T(yK,RK,KX2),…,T(yK,RK,K·X2r)然后对其中的距离T(·)进行从小到大排序：

T(yK,RK,KXi1)

T(yK,RK,KXii)<…

(13)

其中，i1,i2,…,i2r∈2r。

选择距离增量最小的M个T(yM,RM,MXi1)对应的Xi1作为第K维的信号点，进行向下搜索，下面的每一维在选取信号点时都按照这种方式进行，如果在某一维距离增量之和已经大于ρ，那么该维度上的其他信号点就不必搜索，回溯到上一维，继续进行搜索。如果直到D=1时沿这条搜索路径的距离增量和不大于ρ，那么保存下这条路径，同时以此时的距离增量和去替换ρ值。

以QPSK调制为例，基于M算法的贪心策略球形译码算法的搜索树如图3和4所示，M的值分别为1和2，虚线圆圈里面的点是这次搜索中，离发送端最近的M个节点，即距离最小的M个星座点，每一次搜索都从距离增量中选取最小的M个星座点向下搜索，直到搜索结束。

图3 QPSK调制下的SDBGS-M算法的搜索树(M=1)

图4 QPSK调制下的SDBGS-M算法的搜索树(M=2)

4 仿真性能分析

本文通过仿真将SDBGS-M算法与SD算法在相同信道模型下的译码复杂度和误码率性能进行了比较。仿真中，M取值1或者2，译码复杂度以平均访问的节点个数为度量。本文对QPSK、16QAM这2种调制方式和4×4、8×8这2种天线配置下的算法性能和复杂度进行比较，仿真参数如表1所示。

表1 仿真参数表

仿真参数取值天线配置4×4&8×8OFDM符号数14信号检测算法SDBGS-M算法M1或2调制方式QPSK&16QAM带宽20MHz无线信道噪声0～20dB

图5和图6分别为4×4和8×8 MIMO系统下传统信号检测算法与SDBGS-M算法的误码率性能比较图。可以看出，在相同信噪比和天线配置下，传统球形译码算法和基于贪心策略的球形译码检测算法的性能在高阶调制下要低于低阶调制；在相同信噪比和相同调制方式的配置下，多天线会增加系统的信噪比。其次由于SDBGS算法是深度优先搜索球形译码检测算法的一个变形，其只是对搜索点进行了排序，然后选择该层信号集合中距离增量最小的信号点向下搜索，所以SDBGS-M算法性能与SD算法差距不大，但算法复杂度要少很多。

图5 4×4天线，不同调制方式下算法性能对比

图6 8×8天线，不同调制方式下算法性能对比

图7和图8分别表示4×4和8×8 MIMO系统QPSK调制下的SD算法与SDBGS算法检测复杂度比较。从图可以看出，SDBGS-M算法的复杂度相比于传统球形译码算法均有不同程度的降低。特别是在低信噪比区域，有很大的优势，对于4×4天线和QPSK调制下，当SNR=0,M=1,2时，分别为169，119和70，SDBGS-1比球形译码算法的搜索点数减少了50个搜索点数，约占前者的1/3，SDBGS-1算法的检测复杂度比传统SD算法减少22%左右。对于8×8 QPSK系统能减少28%左右。因此，在高阶调制下，基于贪心策略的球形译码检测算法有非常高的系统增益。

图7 4×4天线算法复杂度分析

图8 8×8天线算法复杂度分析

基于贪心策略的球形译码算法有个缺点：在选择符号之前必须首先计算出这一层所有星座点到接收符号的距离，选取最小值对应的符号，排序需要消耗一些时间，因此在实际项目中，选取M=1获得更少的时间开销。

图9是两种算法在4×4 MIMO系统中QPSK调制下译码过程的搜索半径收敛示意图。图中曲线①是SDBGS-1的搜索半径收敛曲线，曲线②是球形译码算法的搜索半径收敛曲线，r是最优解的欧氏距离值，K是球形译码算法初始搜索半径值，基于贪心策略的球形译码算法初始搜索半径为无穷大。从图中可以看出，基于贪心策略的球形译码算法的搜索半径收敛速度明显快于球形译码算法的收敛速度，这就是基于贪心策略的球形译码算法计算复杂度低于球形译码算法的本质原因。SDBGS-1算法相比传统SD算法节省约30%的译码时间。

图9 SD算法和SDBGS-1算法的搜索半径收敛图

基于贪心策略的球形译码算法的性能虽然没有达到ML算法的性能，但该算法通过贪心策略选取局部最优点，加快了搜索半径的收敛速度，从而减少了不必要的搜索点数，降低了计算复杂度。同时基于贪心策略的球形译码算法不需要提前计算出一个初始搜索半径，因此该算法有效缩减了译码时间，大大降低了球形译码的复杂度。而且在低信噪比范围内，随着天线数和调制阶数的增加，基于贪心策略的球形译码检测算法的优越性越大。

5 小结

本文提出了一种基于贪心策略的球形译码检测算法，它是深度优先的球形译码检测中的一种变形。该算法对搜索点进行了排序，然后通过贪心策略选取局部最优点向下搜索，从而减少了不必要的搜索点数，加快了搜索半径的收敛速度，降低了计算复杂度。仿真结果表明，特别是在低信噪比和高调制阶数条件下，SDBGS算法检测复杂度对比传统球形译码有明显优势且容易实现，可以运用于大规模MIMO系统中。

[1] 陈发堂，梁涛涛，李小文.LTE-A系统中球形译码检测算法研究[J].电子技术应用，2012(1)：85-89.

[2] 袁东东，仇润鹤.基于LTE系统的一种低复杂度的球形译码算法[J].通信技术，2015，48(2)：151-155.

[3] 解志斌，邹维辰，薛同思.一种低复杂度的MIMO系统球形检测算法[J].船舶科学技术，2013，35(8)：28-33.

[4] 王秋芳，袁东锋，梁道雷. 一种求解TSP的贪心遗传算法[J]. 制造业自动化，2013，43(2)：162-168.

[5] FU W H，ZHAO C B，WEI W. Improved sphere decoding algorithm in TD-LTE system[C]// 2011 IEEE 3rd International Conference on Communication Software and Networks (ICCSN).[S.l.]：IEEE，2011：514-517.

[6] SHIM B，KANG I.On further reduction of complexity in tree pruning based sphere search[J].IEEE transactions on Communications，2010，2(58)：417-422.

[7] KIM M，KIM J. Applications of SDR exact-ML criterion to tree-searching detection for MIMO systems[C]//2014 8th International Conference on Signal Processing and Communication Systems (ICSPCS). [S.l.]：IEEE，2014：1-7.

[8] LI S P，WANG L，CHEN F C. Ordered sphere decoding detection algorithm for MIMO systems[C]//Control and Decision Conference. [S.l.]：IEEE，2012：3322-3325.

[9] MRINALEE S，GARG H-P，MATHUR G，et al. Improved radius selection in sphere decoder for MIMO System[C]//2014 International Conference on Computing for Sustainable Global evelopment. [S.l.]：IEEE 2014：161-165.

[10] Sonoda Y ，Hua-An Zhao ，Improved Sphere Decoding Algorithm with Low Complexity for MIMO Systems[C]//2014 IEEE/CIC International Conference on Communications in China (ICCC). [S.l.]：IEEE，2014： 11-15.

[11] SONODA Y，ZHAO H A. Improved sphere decoding algorithm with low complexity for MIMO systems[C]// 2014 IEEE/CIC International Conference on Communications in China (ICCC). [S.l.]：IEEE，2015：11-15.

责任编辑：许 盈

Signal detection algorithm based on greedy strategy in large-scale MIMO system

CHEN Fatang, YI Run, HUANG Fei

(ChongqingUniversityofPostsandTelecommunications，ChongqingKeyLabofMobileCommunicationsProtocol,
Chongqing400065,China)

In view of the problem that traditional sphere decoding performance and the computational complexity are restricted by the initial radius and the search strategy, a new greedy strategy sphere decoding detection algorithm based on M algorithm is presented in this paper and the tree search method is improved. Firstly, the distance increment of the signal set in the layer is ordered, and thenMpoints with incremental distance minimum are selected as signal points, so that each selected signal point is locally optimal in the layer. Simulation results show that, compared to the traditional sphere decoding algorithm, the computational complexity can be reduced about 30% by the algorithm when theMis 1. The efficiency of the sphere decoding algorithm is greatly improved and can be also used to the massive MIMO.

signal detection; sphere decoding; greedy strategy; M algorithm

陈发堂，易润，黄菲. 基于贪心策略的大规模MIMO系统信号检测算法[J].电视技术，2017，41(1)：27-31. CHEN F T，YI R，HUANG F. Signal detection algorithm based on greedy strategy in large-scale MIMO system [J].Video engineering，2017，41(1)：27-31.

TN915

A

10.16280/j.videoe.2017.01.006

重庆市教委科学技术研究项目(KJ1500428)

2016-05-24