MIMO中继下行通信系统中的多目标优化设计

代延梅，吴 苏

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

MIMO中继下行通信系统中的多目标优化设计

代延梅，吴 苏

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

针对通信系统中系统功率消耗和接收信号均方误差(MSE)存在冲突关系，无法同时达到性能最优的情况，采用多目标优化(MOO)框架联合优化系统功率消耗和接收信号MSE。文中考虑两跳的多入多出(MIMO)放大转发(AF)中继下行通信系统。联合优化形成的多目标优化问题是非凸且难以直接求解的，为此，提出一种基于帕累托最优策略的资源分配方法，该方法采用加权切比雪夫法，并引入中继预编码矩阵的一般结构和Schur补引理将优化问题转化为SDP问题。仿真结果验证了所提出方法的有效性，表明其具有更好的性能，同时也给出了系统功耗和MSE性能之间的帕累托最优边界。

多入多出(MIMO)；多目标优化(MOO)；放大转发中继；最小化均方误差(MMSE)

近年来，多入多出(Multiple-Input Multiple-Output, MIMO)技术因为能够大大增加系统的分集增益和复用增益而得到了广泛的应用[1]。而协作通信在扩大系统覆盖范围和提高系统容量中发挥了巨大的作用，在中继的三种转发方式中，放大转发(Amplify-Forward, AF)中继由于其简单的处理方式和较短的处理时延而具有更大的发展潜力[2-3]。

联合MIMO和AF中继能够获得两种技术的优点，且已经在许多文献中有了研究[4-8]。在文献[4-7]中，作者旨在系统功率消耗的约束下最小化接收端估计信号与原始信号之间的MSE。与此相反，文献[8]研究在源端和中继端消耗的总功率的约束下，对接收端估计信号的MSE进行优化设计。显而易见，系统功率消耗和接收信号MSE是信息传输系统的两个重要性能，应同时考虑。

多目标优化(Multi-Objective Optimization, MOO)框架可以达到相互冲突的目标之间的平衡[9-11]。在文献[9]中，作者旨在联合优化通信系统的上行链路传输功率和下行链路传输功率，并达到两者之间的均衡。文献[10]采用了多目标优化框架来达到通信系统中的三个性能指标之间的均衡且给出了帕累托最优集。在文献[11]中，作者分析了多目标优化的重要性和必要性，并将多目标的理论和框架应用于5G网络中，旨在对5G网络中各个性能指标之间进行权衡。目前，在两跳MIMO中继通信系统的传输设计中系统功耗或MSE只给出单目标的优化设计，但是对于联合两者进行多目标优化达到两者之间均衡的情况，还没有文献给出具体的研究设计。

基于上述的情况，本文研究两跳MIMO中继下行通信系统中的传输设计，考虑到系统功率消耗和MSE之间存在冲突关系，使得两者不能同时获得最优解的情况，采用多目标优化框架来联合优化系统功率消耗和MSE，达到两者之间的均衡。多目标优化问题中目标函数和约束函数的非凸性和复杂性使得问题不能直接求解，为此，本文提出一种基于帕累托最优策略的资源分配方法。仿真结果中，通过改变性能偏好参数的值获得系统功率消耗和MSE之间的帕累托最优边界。

1 系统模型与优化问题描述

1.1 系统模型

如图1所示，本文研究一个MIMO中继下行通信系统。该系统由一个配置Ns>1根天线的发送端、一个配置Nr>1根天线的中继端和一个配置Nd>1根天线的接收端构成。对于中继端，采用放大转发的工作模式。忽略发送端到接收端的直接链路，因此，通信过程可分为两个阶段。假设所有端均可获取信道状态信息。

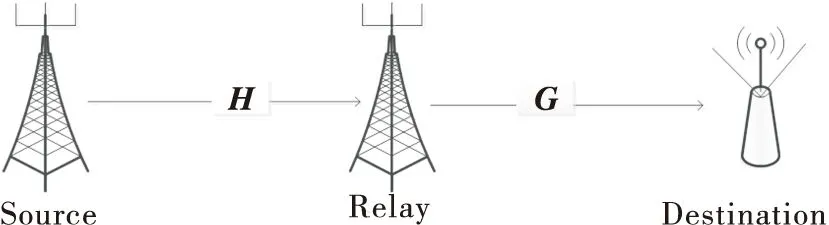
图1 MIMO中继下行通信系统

信息传输第一阶段，发送端对数据向量s∈CNb×1进行预编码处理得到发射信号x=Fs，并将预编码之后的发射信号x发送给中继端。中继端的接收信号可以表示为

yr=HFs+nr

(1)

式中：Nb的选择应该满足条件Nb≤min(Ns,Nr,Nd)；H∈CNr×Ns表示发送端和中继端之间的信道矩阵；F∈CNs ×Nb表示对发送信号进行预编码而产生的预编码矩阵；nr∈CNr×1表示中继端零均值单位方差的加性高斯白噪声。本文假设发送数据向量满足条件E(ssH)=INb。

信息传输第二阶段，中继端将接收到的信号yr进行预编码处理得到xr=Qyr，然后将xr传输给接收端。接收端的接收信号可以表示为

yd=GQHFs+GQnr+nd=GQHFs+n

(2)

式中：Q∈CNr ×Nr表示中继端对接收信号进行预编码处理的预编码矩阵；G∈CNd×Nr表示中继端到接收端的信道矩阵；nd∈CNd×1表示接收端的零均值单位方差的加性高斯白噪声；n=GQnr+nd表示接收端的等价噪声向量。

在接收端采用线性滤波对原始信号进行估计，估计矩阵用W∈CNd×Nb表示，估计信号可以描述为

(3)

1.2 优化问题描述

在本系统中，发送端消耗的功率Ps可以表示为

Ps=tr(FFH)

(4)

中继端消耗的功率Pr可以表示为

Pr=tr(Q(HFFHHH+INr)QH)

(5)

(6)

将式(2)、(3)代入式(6)，可以得到

MSE= tr{(WHGQHF-INb)(WHGQHF-INb)H+

WHRnW}

(7)

式中：Rn=E[nnH]=GQQHGH+INd表示噪声的协方差矩阵。

在实际的通信系统设计中，接收信号MSE和系统功率消耗均为评估系统性能的重要参数。在本节中，首先考虑两个问题的单目标优化设计，然后联合两个问题进行多目标优化设计。其中，第一个优化问题是系统在发送端和中继端消耗的总功率的最优化设计，可以表示为

问题1：(最小化系统总消耗功率)

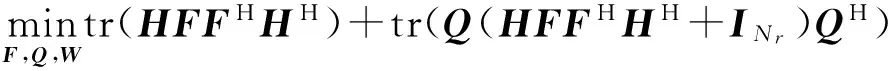
(8)

式中：约束C1中的Pmax表示系统总功率消耗的上限；约束C2中的εmax表示系统允许的最差MSE性能。

第二个问题研究接收信号MSE性能的最小化设计，相应的描述可以表示为

问题2：(最小化接收信号MSE)

WHRnW)

s.t. C1～C2

(9)

在实际应用中，系统功率消耗和接收信号MSE往往是两个必不可少的重要性能。但是两者之间往往是耦合甚至冲突的关系，得到一方面性能提高的同时往往会使得另一方面性能下降。为此，本文采用多目标优化框架并利用帕累托最优策略和加权切比雪夫方法实现两个性能指标之间的均衡，且通过变化性能偏好系数得到最优帕累托边界。问题3可以表示为

问题3：(多目标优化问题—利用加权切比雪夫方法)

s.t.C1～C2

(10)

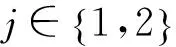
2 资源分配算法

本节中联合优化发送端的预编码矩阵F，中继端的预编码矩阵Q，接收端的估计矩阵W。不管是在目标函数还是在约束中，变量之间都是耦合的，且问题是非凸的，导致无法直接求解出变量的值。为此，本文提出一种复杂度较低的资源分配方法来求解问题并得到变量值。

在接收端，采用著名的线性MMSE滤波器[13]对接收信号进行估计。因此，对于估计矩阵W，可以将其表示为

W=(GQHFFHHHQHGH+Rn)-1GQHF

(11)

将式(11)代入式(6)，同时利用矩阵求逆引理(A+BCD)-1=A-1-A-1B(DA-1B+C-1)-1·DA-1，这样，接收端的MSE可以表示为

MSE= tr(INb-FHHHQHQHGH(GQHFFHHHQHGH+

QHF]-1)

(12)

因此，优化问题1变化为

变换问题1：

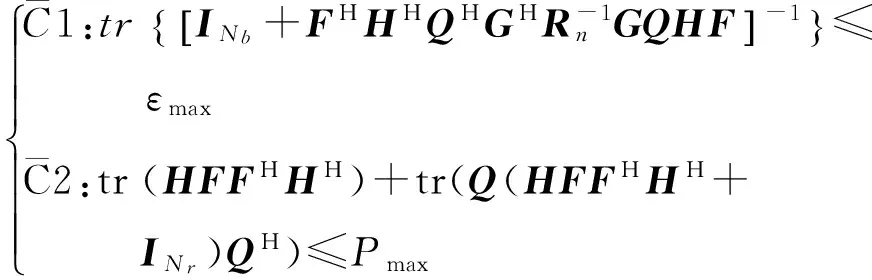
(13)

同理，问题2可以表示为

变换问题2：

(14)

最后，问题3变化为

变换问题3：

(15)

其中，t为辅助优化变量。

接下来，采用具有一般结构的最优中继预编码矩阵Q[6]，Q的结构描述为

Q=TDH

(16)

其中，D=(HFFHHH+INr)-1HF。实际上，整个传输过程可以分为两个部分。D可以看作是第一部分在中继端使用MMSE滤波器时的信号估计矩阵，而T可以看作第二部分中继端发送信号的预编码矩阵。

利用中继端的预编码矩阵Q的结构(式16)，接收信号的MSE表示为

MSE= tr([INb+FHHHHF]-1)+

(17)

在引入中继端预编码矩阵的一般结构之后，中继端的发送信号为zr=DHyr。与式(17)右端的第一部分类似，可以得到

(18)

同理，可得中继端的功率消耗为

Pr= tr(Q(HFFHHH+INb)QH)=

tr(TFHHH(HFFHHH+INr)-1HFTH)=

tr(TRTH)

(19)

利用矩阵求逆引理，zr的协方差矩阵R可以转化为

R=FHHH(INb-HF(FHHHHF+INb)-1FHHH)HF=

FHHHHF(INb-(FHHHHF+INb)FHHHHF)=

FHHHHF(FHHHHF+INb)-1

(20)

(21)

Pr=tr(FFH)+tr(TTH)

(22)

由于MSE的非凸性，通过上面的转换依然不能够求解。为了解决这一问题，本文引入Schur补引理。

引理1(Schur补[15])：对于一个分块矩阵Φ，有

(23)

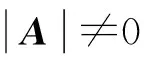
S≥0Φ≥0且A≥0

(24)

下面，利用引理1，可以将问题转化为可以利用CVX解决的SDP问题。

引入X≥[INr+HMHH]-1和Y≥[INd+GNGH]-1。其中，M=FFH，N=TTH。根据引理1，可以得出

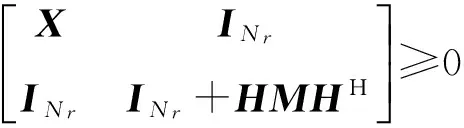
(25)

同理，可以得出

(26)

基于上面的理论，可以得出原优化问题的等价问题。

等价问题 1：

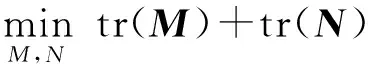
(27)

等价问题 2：

C^1～C^4

(28)

等价问题 3：

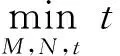
(29)

从式(29)中可以看出，等价问题(27)～(29)为能够被CVX工具解决的SDP问题[16]。同时，通过特征值分解可以获得预编码矩阵F*和T*的最优解，相应的预编码矩阵Q也可以获得。详细的资源分配方法如下：

算法1：帕累托资源分配方法

1)给定初始值λ=0；δ(步长)；

2)求解单目标等价问题1(式(27))和等价问题2(式(28))；

3)根据步骤2)中的结果求解等价问题3(式(29))；

4)λ=λ+δ；

5)重复步骤2)～4)，直到λ=1；

6)对矩阵M和N进行特征值分解，得到发送端和中继端的预编码矩阵F和T。

3 仿真结果

本节中，通过多次仿真来验证所提出方法的可行性和有效性。对于仿真环境，本文选择瑞利平衰落信道。由发送端到中继端的信道矩阵H是均值为零、方差为1/Ns的瑞利衰落信道，由中继端到目的端的信道矩阵G为零均值和方差为1/Nr的瑞利衰落信道。本文中保证接收端估计信号的MSE性能优于εmax=1，天线数选为Ns=Nb=Nr=Nd=3。仿真结果通过对信道的1 000次平均获得。图2通过变化性能偏好系数λj给出不同系统性能之间的帕累托最优边界，这里λj的步长取δ=0.05。

图2 平均系统总功率消耗和平均MSE之间的帕累托边界

图2描述不同方法下系统在发送端和中继端的系统总功率消耗和接收端估计信号MSE之间的均衡。在仿真中，系统总功率消耗最大预算设置为Pmax=40 dB。对于NAF(amplify-and-forward)方案，用常数和单位矩阵的乘积来代替预编码矩阵F和T。从图中可以看出，MSE是随着总功率消耗的增长而单调减小，这也说明在通信系统中MSE和总功率消耗之间存在的冲突关系。在实际的系统设计中，设计者可以根据其对系统性能的偏好性来选择偏好系数的值。图2也验证了本文提出方案的性能是优于NAF方案的。

图3描述不同方法下系统在发送端和中继端的总功率消耗和系统误比特率(Bit Error Rate, BER)之间的均衡。为了更清楚地显示两者之间的关系，图3对BER轴采用对数坐标。图3揭示了总功率消耗和BER之间的冲突关系，且给出了两者之间的最优帕累托边界。图3也验证了本文提出方案的性能优于NAF方案。

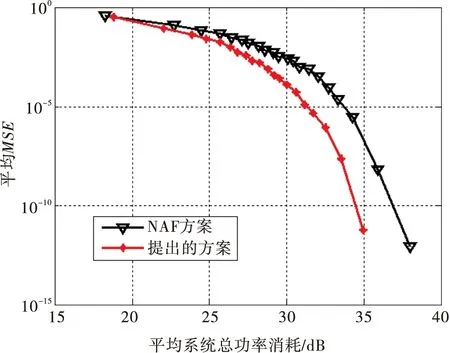
图3 平均系统总功率消耗和平均BER之间的帕累托边界

图4描述了发送端的功率消耗和接收信号MSE之间的均衡。在仿真中，约束中继端的最大功率消耗，而联合优化发送端的功率消耗和接收信号MSE，分别将中继端的功率设为Pr=20 dB和Pr=40 dB，而将发送端的最大功率预算设为30 dB。从图中可以看出，MSE是随着发送端功率消耗的增长而单调减小，揭示了发送端功率消耗和BER之间的冲突关系。中继端发送功率为40 dB的情况会优于20 dB的情况，且文中提出的方案性能优于NAF方案。

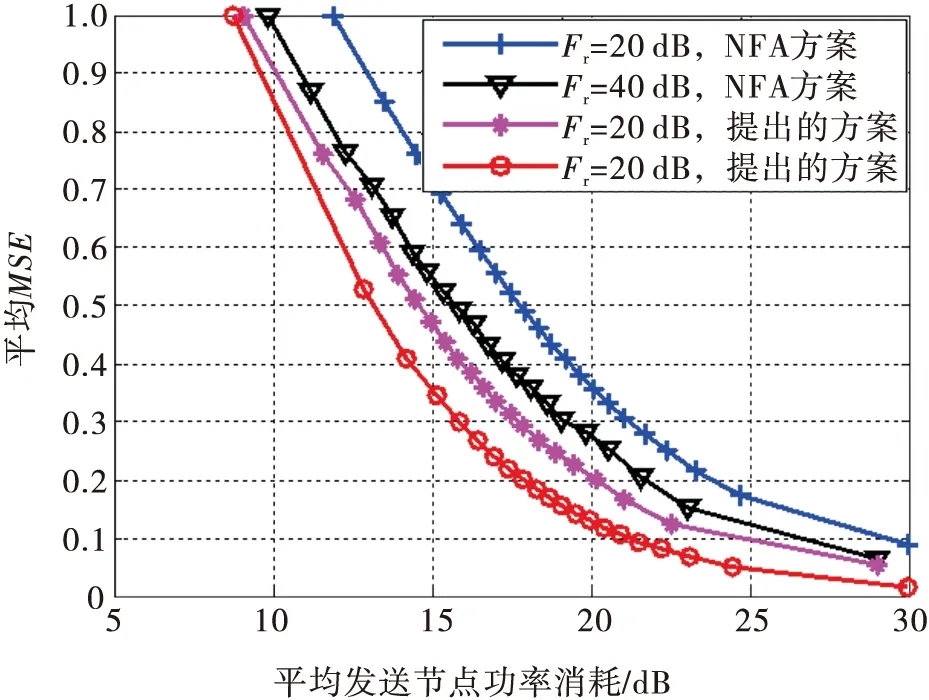
图4 平均发送端功率消耗和平均MSE之间的帕累托边界

4 总结

本文研究了MIMO两跳AF中继下行通信系统中系统功率消耗和接收信号MSE之间的冲突问题。采用多目标框架来对通信问题建模，得到多目标优化问题。由于多目标优化问题是非凸且难以解决的，采用加权切比雪夫方法，并引入中继预编码矩阵的一般结构和Schur补引理将问题转化为SDP问题。最后，仿真结果验证了所提出方案的性能，并给出了不同系统参数之间的帕累托最优边界。下一步的工作将考虑非理想信道的情况来增强系统的健壮性。

[1] VISHWANATH S, JINDAL N, GOLDSMITH A. Duality, achievable rates, and sum-rate capacity of Gaussian MIMO broadcast channels[J]. IEEE transactions on information theory, 2003, 49(10): 2658-2668.

[2] LANEMAN J N, TSE D N C, WORNEL G W. Cooperative diversity in wireless network: efficient protocols and outage behavior[J]. IEEE transactions on information theory, 2004, 50(12): 3062-3080.

[3] TANG X J, HUA Y B. Optimal design of non-regenerative MIMO wireless relays[J]. IEEE transactions on wireless communications, 2007, 6(4): 1398-1407.

[4] KHANDAKER M R A, RONG Y. Precoding design for MIMO relay multicasting[J]. IEEE transactions on wireless communicaitons, 2013, 12(7): 3544-3555.

[5] SINGH V P, CHATURVEDI A K. Min-max mean squared error-based linear transceiver design for multiple-input-multiple-output interference relay channel[J]. IET communication, 2015, 9(6): 853-861.

[6] RONG Y. Simplified algorithms for optimizing multiuser multi-hop MIMO relay system[J]. IEEE transactions on wireless communications, 2010, 59(10): 2896-2904.

[7] ZHAO C, CHAMPAGNE B. A unified approach to optimal transceiver design for nonregenerative MIMO relaying [J]. IEEE transactions on vehicular technology, 2015, 64(7): 2938-2951.

[8] HE Z, LANG Z, RONG Y, et al. Joint transceiver optimization for two-way MIMO relay system with MSE constraint[J]. IEEE wireless communications letters, 2014, 3(6): 613-616.

[9] SUN Y, NG D W K, SCHOBER R. Multi-objective optimization for power efficient full-duplex wireless communication systems [C]//Proc. 2015 IEEE Global Communications Conference(GLOBECOM). [S.l.]：IEEE, 2015, 1-6.

[10] NG D W K, LO E S, SCHOBER R. Multi-objective resource allocation for secure communication in cognitive radio networks with wireless information and power transfer[J]. IEEE transactions on vehicular technology, 2015, 65(5): 3166-3184.

[11] BJORNSON E, JORSWIECK E, DEBBAH M, et al. Multiobjective signal processing optimization: the way to balance conflicting metrics in 5G systems [J]. IEEE signal processing magazine, 2014, 31(6):14-23.

[12] MARLER R T, ARORA J S. Survey of multi-objective optimization methods for engineering[J]. Struct. multidisc optim., 2004, 26(6): 369-395.

[13] KAY S M. Fundamentals of statistical signal processing: estimation theory[M]. Englewood Cilffs, NJ: Prentice Hall, 1993.

[14] SONG C, LEE K, LEE I. MMSe based transceiver designs in closed-loop non-regenerative MIMO relaying systems[J]. IEEE transactions on wireless commun., 2010, 9(7): 2310-2319.

[15] BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge, U. K.: Cambridge University Press, 2004.

[16] GRANT M, BOYD S. CVX: Matlab software for disciplined convex programming[EB/OL]. [2016-04-10]. http://cvxr.com/cvx/.

[17] PALOMAR D P, CIOFFI J M, LAGUNAS M A. Joint Tx-Rx beamforming design for multicarrier MIMO channels: a unified framework for convex optimization[J]. IEEE transactions on signal process, 2003, 51(9): 2381-2401.

代延梅(1990— )，女，硕士生，主研无线协作通信、MIMO网络、多目标优化等；

吴 苏(1992— )，女，硕士生，主研物理层安全、多目标资源优化等。

责任编辑：薛 京

Multi-objective optimization design for MIMO relay downlink systems

DAI Yanmei, WU Su

(CollegeofTelecommunication&InformationEngineering,NanjingUniversityofPostsandTelecommunications,Nanjing210003,China)

As the coupled and even conflicting relationship between the system power consumption and the minimum mean-squared error (MSE) at the receiver, a multi-objective optimization (MOO) framework for optimizing system power consumption and MSE jointly is adopted. A two-hop multiple-input multiple-output (MIMO) amplify-forward (AF) relay downlink system is considered in this paper. Since the formulated MOO problem (MOOP) is non-convex and hard to tackle, a Pareto resource allocation method is proposed by exploiting the weighted Tchebycheff approach, the optimal structure of the relay precoding matrix and the Schur complement. Simulation results not only demonstrate the effectiveness of the proposed algorithm, but also unveil an important trade-off between power consumption and MSE at the receiver.

MIMO; multi-objective optimization (MOO); AF relay; minimum mean-squared error (MMSE)

代延梅，吴苏.MIMO中继下行通信系统中的多目标优化设计[J]. 电视技术，2017,41(1)：58-63. DAI Y M, WU S.Multi-objective optimization design for MIMO relay downlink systems[J]. Video engineering，2017,41(1)：58-63.

TN929.5

A

10.16280/j.videoe.2017.01.012

国家自然科学基金项目(61271232)；国家移动通信研究实验室开放研究基金(2012D05)

2016-05-29