基于哈夫变换的根系分布率计算

黄晓然，钟伟钊，徐小红，杜志发，朱同林

(华南农业大学 数学与信息学院，广东 广州 510642)

基于哈夫变换的根系分布率计算

黄晓然，钟伟钊，徐小红，杜志发，朱同林

(华南农业大学 数学与信息学院，广东 广州 510642)

通过数码摄像机绕拍摄植物根系一周得到多幅二维图像，定量分析植物根系的三维构型。通过拍摄所得的三维图像，利用图像分割算法和骨架抽取算法，提取根系细化后的拓扑结构，然后根据广义哈夫变换，计算出根系各点旋转所得的椭圆的相关参数，再利用椭圆的右端点，计算得到根系在不同介质层和介质方向的分布情况，并在此基础上，提出一种改进的方法快速确定椭圆参数空间，大幅提升椭圆检测的速度，使得根系的三维构型定量分析可以真正应用于农业领域研究中，为农学家进一步研究植物根系及植物间作套种提供技术支撑。

根系；椭圆检测；哈夫变换；参数空间；三维构型

根系是作物获取水分和养分的重要器官，由于土壤的观测阻碍，根系三维形态的认知与表达成为作物根系深入研究的瓶颈。三维数字化、可视化是研究和认知作物形态结构的重要方法，研究具有表征根系长相长势及土壤中水分、养分等物质对作物根系构型的影响具有重要意义。

20世纪初期，Cannon在关于植物根系为适应荒漠环境而导致的根系形态结构变异的研究中，首次提出根构型(root architecture)一词，之后许多研究根系的文章开始沿用该词[1]。目前，尚无用于定量描述植物根系三维立体几何构型的综合指标。定量分析植物根系三维结构，有助于人们发现植物根系形态结构对于植物抗逆性的重要作用，能为育种家发现优势性状、培育优良品种等提供理论依据。然而，根系的三维结构复杂，次根交错重叠互相遮挡，给测量工作带来诸多不便。目前已经报道的获取三维根构型图像的主要方法有以下几种：X射线断层扫描技术(CT)、核磁共振成像(MRI)、地下雷达监测(GPR)和计算机视觉等[2-4]。其中，GPR系统只适于较粗的根系，如大树的根系，对于大豆等作物的根系并不适合；MRI和CT两种方法的设备昂贵且不易操作，一般用于医学方面居多，不适于大量实验。计算机视觉方法通过使用多个摄像头获取根系的不同角度的二维图像，建立图像模型，实现了对三维根系构型的图像重建，但三维重建过程需要进行摄像机定标。截至目前，尚无完善的方法实现精确的定标，图像重建结果精度较低，导致根系拓扑结构的计算结果与实际测量存在较大差异。徐小红等(2011)利用广义哈夫变换原理研究了在特殊拍摄条件下根系在介质各层次和各方向分布率[5]，但由于椭圆待确定参数较多，检测速度比较慢。

本文进一步研究了根系拓扑结构，由于根系的旋转轨迹呈椭圆形状，因此利用哈夫变换，将椭圆映射到哈夫空间，通过设置累加器，投票获得根系各点旋转一周得到的椭圆的各个参数，然后根据椭圆的右端点位置，就能快速计算出根系在不同介质层和介质方向的分布率，并在此基础上，利用椭圆的特性，快速确定椭圆参数范围，此算法效率也得到显著提高。

1 理论基础

1.1 哈夫变换

哈夫变换是图像处理中从图像中识别目标形状的基本方法之一，把在图像空间的检测问题转换到参数空间里，通过在参数空间里进行简单的累加统计完成检测。设在图像空间有一个目标 ，其几何形状可用代数方程表示，通过使用哈夫变换可以直接对图像中已知形状(如直线、圆等)的目标进行边缘检测，或是利用图像的全局特性，将目标边缘像素连接成有意义的边缘，形成目标的封闭区域边界。哈夫变换具有全局性，计算量小，可以适用于不规则曲线，不容易受噪声和边界的影响，具有较好的抗干扰性[6]。

已知的直线方程为

y=ax+b

(1)

在哈夫变换中，方程可以转化为极坐标形式

d=ρsin(θ-φ)=xsinθ-ycosθ

(2)

其中：d为直线到坐标原点的垂直距离；θ是直线与极轴正向的夹角；ρ是极径；φ是极径与极轴的夹角，x，y是图像点的直角坐标[7]。直线的极坐标形式如图1所示。

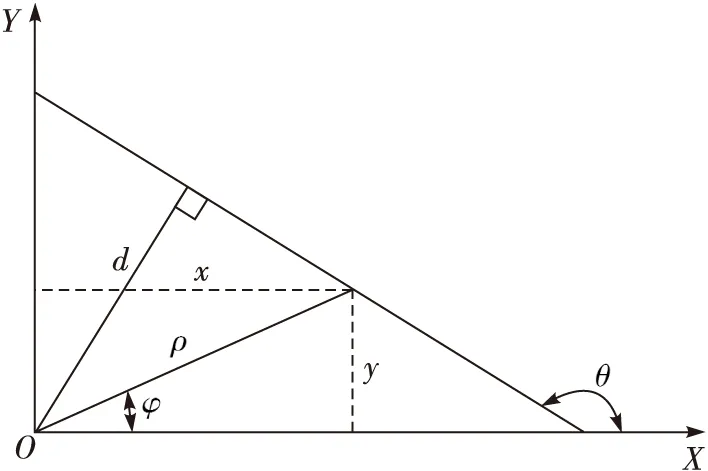
图1 直线的极坐标形式

实际应用中，将(d，θ)离散化，设置累加器，以存储图像中各点在参数空间中的信息，由于图像空间中的直线相应地对应于参数空间中的点，因此在二维累加器中，统计各点数值后，找到超过一定阈值的峰值点，就是图像空间中的直线。

通过哈夫变换，图像空间中的直线映射到于参数空间中的点，在二维累加器中计算各点累加结果，找到峰值超过某个阈值的点，即对应图像空间中的直线。

将哈夫变换应用到一般曲线(如圆、椭圆，或者解析式未知的曲线等)，称为广义的哈夫变换。随着曲线待定参数数量的增加，累加器所需的空间和计算时间呈指数递增，利用哈夫变换计算曲线参数变得尤为复杂。因此，需要通过其他方法降低待定参数维度，减小参数的取值范围，以此减少计算量，提高检测速度[8]。

1.2 椭圆方程

椭圆的一般方程形式如下：

ax2+bxy+cy2+dx+ey+1=0

s.tΔ=b2-4ac<0

(3)

为了确定椭圆的几何位置，利用坐标旋转和平移变换把椭圆一般方程化成标准方程

(4)

其中，几何中心为

(5)

倾斜角弧度为

(6)

长半轴为

(7)

短半轴为

(8)

由此得到椭圆参数方程

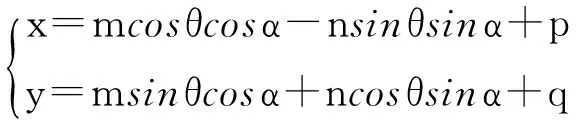
(9)

则根据椭圆上点(x,y)对应的角度参数α就能找到相隔β角度的下一个点的位置(x′,y′)，即

(10)

1.3 图像分割和细化

阈值法是一种简单有效的图像分割方法[9]，通过使用多个阈值，将图像按照灰度级分割成几个部分，同一个部分的像素被认为是属于同一个物体。阈值法包括双峰法、OTSU、时刻存储法、最小错误法[10-13]等方法。阈值法的最大优点是计算量小，实现简单，在运算效率优先的场合(如用于硬件实现)中得到了广泛的应用。

本文采用最小错误法，将图像中的像素点分为前景和后景两部分，实现图像的二值化。

骨架是物体形状或轮廓的一维简化表示方式，它可以无失真地表示原始物体的拓扑结构。自Blum最先提出骨架化的概念以来，数十年间大量学者从各个方向研究了骨架的各种特性，骨架化也被广泛应用到各类型的研究领域之中。目前，离散域骨架的算法主要包括以下三种：一是拓扑细化的方法，此方法是目前研究最多、最成熟的方法。主要步骤是迭代地删除目标的边缘点，直到只剩一个像素点，如此可以得到连续的骨架，但边界噪声会对骨架化结果造成较大干扰，因此容易产生冗余的分支，骨架的位置可能会偏离物体的中心，由于需要多次迭代，对于数据量较大的图像处理效率比较慢。二是基于距离变换方法，通过距离变换，得到图像梯度的梯度值，将梯度值的局部最大值连接起来形成骨架，此类方法得到的骨架处于物体中心，但骨架的连通性较差，会产生断裂现象[14-15]。 三是基于Voronoi图方法[16-18]。Voronoi图一般用于数字几何物体，是中轴的包集，生成骨架过程中需要剪枝处理，算法复杂度较高，实现复杂。针对根系的圆柱性状，本文采用拓扑细化的改进方法，提取根系骨架。

2 基于广义哈夫变换的椭圆检测算法

本文使用数码摄像机围绕植物根系旋转一周拍摄所得的视频，且镜头中心对准固定着根系的转台中心，相机镜头与根系顶点平齐， 根系上的某点在旋转过程中，转到距离摄像机镜头右端水平距离最远的位置时，在成像平面上对应为该点旋转所得的椭圆的长轴右端顶点。

由于摄像机在旋转过程中，根系上的点与摄像机的距离会发生变化，造成视觉上的远小近大的现象(图2)，导致拍摄得到的椭圆并不是标准的椭圆，椭圆的上半部分会向上稍微凸起，下半部分同样向上收缩，如图3所示。因此，如果直接使用式(9)～(10)计算根系点的旋转轨迹会有较大的误差。通过实验观察结果，本文引入透视增量μ，即通过透视观察到的旋转角度应为β+μ，其中

(11)

图2 视觉上的远小近大现象

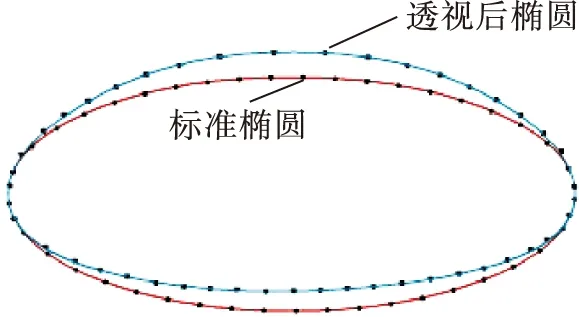
图3 标准椭圆和透视后椭圆

则根据椭圆上点(x，y)计算得到相隔β角度的下个点的位置(x0，y0)的公式变为

x0=acosθcos(α+β+μ)-bsinθsin(α+β+μ)+p

(12)

y0=asinθcos(α+β+μ)-bcosθsin(α+β+μ)+q

(13)

假定第一帧视频对应起始方向，如果当前帧中有前景像素点正好为某个椭圆右端点坐标，则记录此像素点坐标、所在帧和对应椭圆方程，并且根据所在帧和点纵坐标分别推算所处方向角度和所处的小层。

椭圆检测算法的步骤如下：

1)对拍摄所得的视频进行二值化和骨架化处理，得到根系的细化结果。

2)对于每个前景像素点(x0，y0)，分别给予椭圆方程参数(a，b，p，q，θ)一定范围，找到所有符合参数方程的参数(a，b，p，q，θ)。

3)利用式(4)，对其余帧进行投票。根据当前帧的像素点(x0，y0)，利用式(12)和(13)计算出椭圆在下一帧的像素点位置(x1，y1)，如果下一帧内存在像素点位置接近(x1，y1)，则对应参数的得票加1。

4)直到所有帧投票结束，输出票数值最大的参数。

5)重复步骤2)～4)，直到第一帧中所有前景点对应的椭圆计算完毕。

哈夫变换通过投票原理来选择票数超过某个阈值的根系点，这样就解决了根系点互相遮挡的问题，因为在根系旋转过程中，只有很小部分的角度范围会被遮挡，因此根系点在少量几张图片帧不出现也不会影响最后的票数入选。

但是，由于椭圆的待确定参数众多，算法的时间复杂度为O(n4)，如果直接以穷举的方式计算椭圆参数，算法的运行效率低下。对此，本文在此方法的基础上，提出了一种新的方法快速确定椭圆参数范围，在不影响精度的情况下，将算法复杂度降低到O(n)。

假设根系的初始位置位于图像的水平中点，根系在旋转过程中，由椭圆的对称性可知，根系上的每个点必然会经过图像正中间，并且该点为椭圆的上端点或下端点，记该点为(x0，y0)，而椭圆的左右端点(x1，y1)，(x2，y2)必然存在于此帧图像旋转过90°和270°的图像帧中，而且(x1，y1)，(x2，y2)关于椭圆的中心对称。

由此，可以大致确定椭圆的参数

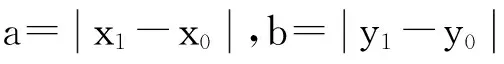
(14)

在此参数的基础上，进行一定误差范围内的遍历投票，选出得票率最高的参数，即为相应点所在的椭圆的参数。

具体步骤如下：

1)对拍摄所得的视频进行二值化和骨架化处理，得到根系的细化结果。

2)对于当前帧的图像，寻找根系在水平方向上处于中心的像素点(x0，y0)，则(x0，y0)为该点所在的椭圆的最上方或者最下方的点。

3)在当前帧转过90°和270°的图像帧分别寻找点(x1，y1)，(x2，y2)，满足以下条件

(15)

4)计算得到椭圆参数为

(16)

5)利用式(4)，对其余帧进行投票。根据当前帧的像素点(x0，y0)，利用式(12)和(13)计算出椭圆在下一帧的像素点位置(x1，y1)，如果下一帧内存在像素点位置接近(x1，y1)，则对应参数的得票加1。

6)所有帧投票结束，输出票数值最大的参数。

7)对于下一帧图像，重复步骤2)～6)，直到所有帧数的一半的图像帧完成。

3 实验结果

根据上述算法笔者进行了2组仿真实验。实验1中拍摄对象是单根系，实验2中拍摄对象是复杂根系，分别如图4和图5所示。

图4 单根系 图5 复杂根系

土壤学家将土壤分为三层：第一层称为表土层，结构松散，呈暗褐色，土壤中的主要成份包括黏土、腐殖质和其他无机物；第二层通常被称为亚土层或亚表层，主要成份为黏土，此外还有少量从上一层淋滤下来的其他微粒组成，几乎不包含腐殖质；第三层称为母质层，主要成份为风化的岩石。不同土壤层对于根系的生长分布有不同影响，因此，相应地将介质层划分为三大层(图6)和八个方向区域(图7)，计算出根系在介质不同层次和方向的分布比率。

图6 介质分层图

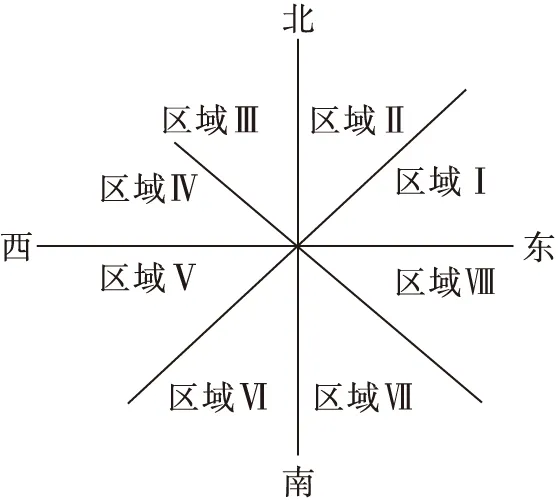
图7 介质分向图

实验是在处理器：Intel(R) Core(TM)2 Duo CPU E7500，主频： 2.93 GHz，3.25 Gbyte RAM的 台式机上进行，利用Visual C++ 编程实现算法，实验1和2所用视频均有26帧图像。运行效果截图如图8～9所示，根系在介质层和介质方向的分布情况见表1和表2。

图8 试验1中根系的原始、细化、整合图片

图9 试验2中根系的原始、细化、整合图片

根系拓扑结构哈夫算法结果/%改进的哈夫算法结果/%实际测量/%介质第一层69.5766.6766.67介质第二层30.4333.3332.57介质第三层000.76区域方向I62.5061.9060.29区域方向II37.5038.1039.71区域方向III000区域方向IV000区域方向V000区域方向VI000区域方向VII000区域方向VIII000运行时间/s122.63.65594

表2 实验2中根系在介质中的分布结果

根系拓扑结构哈夫算法结果/%改进的哈夫算法结果/%实际测量/%介质第一层59.7862.1661.42介质第二层32.1731.8131.56介质第三层8.046.037.02区域方向I32.3831.5035.57区域方向II7.128.868.11区域方向III1.022.891.17区域方向IV4.076.115.63区域方向V13.8514.4413.12区域方向VI12.4211.889.14区域方向VII9.7810.7710.21区域方向VIII19.3517.5517.05运行时间/s950.7325.362376

结果显示，改进的椭圆检测算法和原哈夫算法相比，在精度上相差不多，并且计算结果都与实际测量结果接近，主要的误差来自光照在各角度的不均，导致根系骨架提取过程中根须产生断裂现象。直接使用广义哈夫变换检测椭圆，由于待定的参数较多，实现复杂，运算量很大，算法效率低下。通过利用椭圆的端点，快速缩小待定参数的取值范围，可以大幅减少计算参数过程的时间，算法复杂度降低到O(n)。即使是处理复杂的根系，改进后的算法也可以在很短时间内得到相对精确的结果。

4 小结

本文在基于广义哈夫变换原理和透视原理检测根系点的旋转椭圆轨迹方程的基础上，利用椭圆的特性提出了一种改进的旋转椭圆检测算法，快速确定椭圆参数，大幅提升椭圆检测的速度，最后根据检测到的椭圆右端点性质计算大豆根系在不同介质层的水平和垂直分布比率，使得根系的三维构型定量分析可以真正应用于农业领域研究中，为进一步研究植物根系，培育优良品种提供技术支撑。

由于拍照时光线在各角度不均匀，细化效果存在缺陷，会造成细化视频中有部分根系根产生断裂现象，而改进的椭圆检测算法依赖于特殊点的检测和计算，因此，在今后的工作中，需要改进骨架化提取算法，使根系骨架化结果更加精确；此外，根系还存在许多构型参数需要计算，如主根长、根系分支数基根角度、各分支根长、总长度等参数，希望能在今后的工作继续深入研究。

[1] LYNCH J. Root architecture and plant productivity[J]. Plant physiology，1995，109(1)：7.

[2] 朱同林，方素琴，李志垣，等. 基于图像重建的根系三维构型定量分析及其在大豆磷吸收研究中的应用[J]. 科学通报，2006，51(16)：1885-1893.

[3] 廖红，严小龙. 菜豆根构型对低磷胁迫的适应性变化及基因型差异[J]. 植物学报(英文版)，2000，42(2)：158-163.

[4] 梁泉，廖红，严小龙. 植物根构型的定量分析[J]. 植物学报，2007，24(6)：695-702.

[5] XU X H， LIANG Y J，LIU H C， et al. Plant root length distribution rate calculation in the medium based on Hough transform[J]. Journal of computational and information systems，2011， 8(16)：4217-4224.

[6] 董梁. 基于哈夫变换的图像边缘连接[J]. 现代电子技术，2008，31(18)：149-150.

[7] 邱力为，宋子善，沈为群. 直线参数检测的快速哈夫变换[J]. 北京航空航天大学学报， 2003，29(8)：741-744.

[8] 侯宇. 基于Hough变换的图象检测对偶点法[J]. 中国图象图形学报，2001，6(8)： 746-749.

[9] 韩思奇， 王蕾. 图像分割的阈值法综述[J]. 系统工程与电子技术，2002，24(6)：91-94.

[10] SANG U L， CHUNG S Y， PARK R H. A comparative performance study of several global thresholding techniques for segmentation[J]. Computer vision graphics & image processing， 1990，52(2)：171-190.

[11] JUN O. A threshold selection method from gray-scale histograms[J]. IEEE transactions on system man cybernetics，1988 (1)：62-66.

[12] TSAI W H. Moment-preserving thresolding：A new approach[J]. Computer vision， graphics，and image processing，1985，29(3)：377-393.

[13] KITTLER J，ILLINGWORTH J. Minimum error thresholding[J]. Pattern recognition，1986， 19(1)：41-47.

[14] NIBLACK C W， GIBBONS P B， CAPSON D W. Generating skeletons and centerlines from the distance transform[J]. CVGIP： Graphical Models and Image Processing， 1992， 54(5)： 420-437.

[15] 丁颐， 刘文予， 郑宇化. 基于距离变换的多尺度连通骨架算法[J]. 红外与毫米波学报， 2005，24(4)：281-285.

[16] POGGIO B，BRUNELLI R，POGGIO T. HyberBF networks for gender classification[C]//Proc. the DARPA Image Understanding Workshop. San Mateo：Morgan Kaufmann，1992：311- 314.

[17] BUHMANN J， LADES M， MALSBURG C. Size and distortion invariant object recognition by hierarchical graph matching[C]//Proc. the International Joint Conference on Neural Networks. San Diego：IEEE，1990：411-416.

[18] VAPNIK V N. The nature of statistical learning theory [M]. New York： Springer -Verlag， 1995.

黄晓然(1991— )，硕士生，主研图形图像处理；

钟伟钊(1990— )，硕士生，主研图形图像处理；

徐小红(1975— )，女，博士，主研计算机图形学；

杜志发(1986— )，硕士生，主研图形图像处理；

朱同林(1963— )，教授，博士生导师，主要研究方向为小波分析与计算数学。

责任编辑：闫雯雯

Root distribution measurement based on Hough transform

HUANG Xiaoran， ZHONG Weizhao， XU Xiaohong， DU Zhifa， ZHU Tonglin

(CollegeofMathematicsandInformatics，SouthChinaAgriculturalUniversity，Guangzhou510642，China)

By using a digital camera rotated to the roots， multi-angle two-dimensional images of the plant roots are taken， and the morphological structure of plant roots is quantitative analyzed. Image segmentation algorithms and skeleton extraction algorithm are applied to these three-dimensional images so that the topology of thinned roots is extracted， and then according to the generalized Hough transform， the parameters of the ellipses which are obtained from the rotation of points is calculated. Through the right points of ellipses， root distribution in different media layers and different media direction is calculated. Base on it， an improved method is put up to rapidly estimate the parameters space， significantly increasing the speed of ellipse detection， so that roots quantitative analysis of three-dimensional structure can really be applied to agricultural fields， as agronomists further study of plant roots， provide technical support of varieties cultivation.

root； ellipse detection； Hough transform； parameter space； three-dimensional architecture

黄晓然，钟伟钊，徐小红，等. 基于哈夫变换的根系分布率计算[J].电视技术，2017，41(1)：84-89. HUANG X R， ZHONG W Z， XU X H，et al. Root distribution measurement based on Hough transform[J]. Video engineering，2017，41(1)：84-89.

TP391.41

A

10.16280/j.videoe.2017.01.017

高等学校博士学科专项科研基金联合资助课题(20124404110018)

2016-03-15