光学教材中有关椭圆偏振光知识的分析与解读

杨 静，李韶峰，张利红，朱新颖，王韩奎

(周口师范学院 物理与电信工程学院， 河南 周口 466000)

光学教材中有关椭圆偏振光知识的分析与解读

杨 静，李韶峰，张利红，朱新颖，王韩奎

(周口师范学院 物理与电信工程学院， 河南 周口 466000)

常见的本科光学教材中，在平面简谐电磁波的波函数形式、椭圆偏振光的旋向与两子波的相位差之间的关系、椭圆偏振光的琼斯矢量表达式等知识点上，所给出的推导过程和结论不尽相同，甚至互相矛盾，令学生迷惑、误解. 结合笔者的教学经验，对以上问题进行了对比分析，对各知识点进行了深入梳理，经推导和证明，给出了明确的结论.

波函数；椭圆偏振光；旋向；琼斯矢量

The analysis and interpretation of the knowledge about elliptically polarized light in optics textbooks. Journal of Zhejiang University(Science Edition), 2017,44(1):053-056

振动方向相对于传播方向的不对称性叫作偏振. 光波是电磁波，光波中的电振动矢量E和磁振动矢量H都与传播速度v垂直，因此，具有偏振性的光称为偏振光. 偏振光学是光学领域中一个重要的分支，偏振光在光学显示和光学测试中有着不可替代的作用.

在高等院校本科教学中，光学与工程光学是物理、光电子等理工科相关专业的必修课程.教材版本较多，常见的有玻恩等[1]的《光学原理》、叶玉堂等[2]的《光学教程》、赵凯华[3]的《光学》，郁道银等[4]的《工程光学》、姚启钧[5]的《光学教程》等.以上教材对光的偏振知识的介绍各有侧重点，但在平面简谐电磁波的波函数、椭圆偏振光的旋向判断以及偏振光的琼斯矢量表示等知识点的推导过程及表达形式上略有不同，有的甚至相互矛盾，导致学生迷惑不解.为此，笔者拟对上述教材中椭圆偏振光相关知识存在的差异和矛盾进行对比分析，讨论并厘清其中存在的问题.

1 平面简谐电磁波的波函数表达

由麦克斯韦方程组可以解得电场强度E有多种

形式的解，以最简单的平面电磁波为例，假设平面波沿直角坐标系的z方向传播，其波动方程为[1]：

(1)

其中，v为电磁波的传播速度. 在均匀介质中，如果没有电流和电荷，其解有2种表达形式：

(2a)

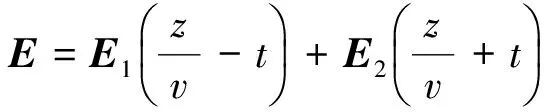
(2b)

对频率为ω的平面简谐电磁波，波动方程的解可写为：

(3)

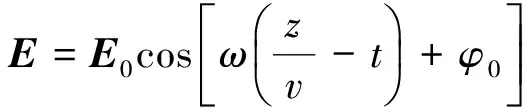
(4)

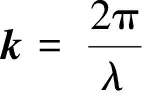
(5)

(6)两式中指数上的正负号代表2种不同的选择，选择任何一种均可，其运算完全等效.文献[2-3]采用式(5)，指数取负号；文献[4-5]采用式(6)，指数取正号.

综上，平面简谐电磁波的波函数计算，各版本选择一致，形式上都可转化为：

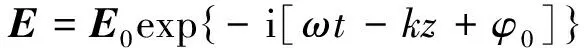
(7)

2 椭圆偏振光的旋向问题

2.1 左右旋偏振光中存在的左右手关系问题

当两列频率相同、传播方向相同、振动方向互相垂直的单色波叠加时，根据两列光波相位差、振幅的关系，合成光可以是线偏振光、圆偏振光和椭圆偏振光. 关于(椭)圆偏振光的旋向规定，4种教材都遵循传统习惯，即迎着光传播方向看，两列光合矢量箭头的末端若是顺时针旋转，则为右旋偏振光. 若以光的传播方向为大拇指方向，四指指向合矢量的旋转方向，此时旋向与传播方向成左手螺旋关系；反之为左旋偏振光，旋向与传播方向成右手螺旋关系[1-2,4-5].

提到左右手关系的，只有姚启钧的《光学教程》. 文中指出：在光的传播方向z上，各点电矢量的相位随z的增加而逐点落后，因此同一时刻沿z方向场中各点电矢量的相对取向与传播方向之间，在右旋椭圆偏振光中，正好构成右手螺旋[5]. 学生往往觉得这与前述矛盾，认为此处“右旋构成右手螺旋”的描述错误. 但需要注意的是，教材中有明确的前提，即某一时刻，各点电矢量的相对取向与传播方向成右手螺旋关系(因相位落后). 而前面提到的右旋偏振光中存在的左手关系，指的是在不同时刻，随着光的传播，合矢量箭头末端旋转出一条轨迹，其旋转方向与传播方向成左手螺旋关系. 所以《光学教程》中的描述是正确的.

2.2 通过相位差判断左右旋偏振问题

通过2列子波的相位差Δφ判断旋向时，一般教材的结论为(即使有的教材没有明确说明，从配图也能看出此结论)：当sinΔφ>0时，为右旋偏振光；当sinΔφ<0时，为左旋偏振光. 而《工程光学》给出的结论以及配图却与此相反. 下面通过简单的证明，说明椭圆偏振光的旋向与相位差的关系. 振动方向垂直的2子波的波函数可以写为：

Ex=a1cos(kz1-ωt)=a1cos φ1，

Ey=a2cos(kz2-ωt)=a2cos(φ1+Δφ).

(8)

通常合成方程为

(9)

式(9)描述的是一个椭圆方程，且Ex∈[-a1,a1],Ey∈[-a2,a2]. 下面通过简单的证明，寻找旋向与相位差正弦值之间的关系.

随着相位的增加，光向z轴正方向传播，自A点转向B点，存在2条路径c和d(图中只标明路径的大致方向，实际上A和B点应该是椭圆上的2个点). 而当φ1∈[0,π/2]时，Ex∈[1,0]，即Ex始终大于0.为符合这一要求，实际路径只能选择顺时针旋转的路径d，则为右旋偏振光.

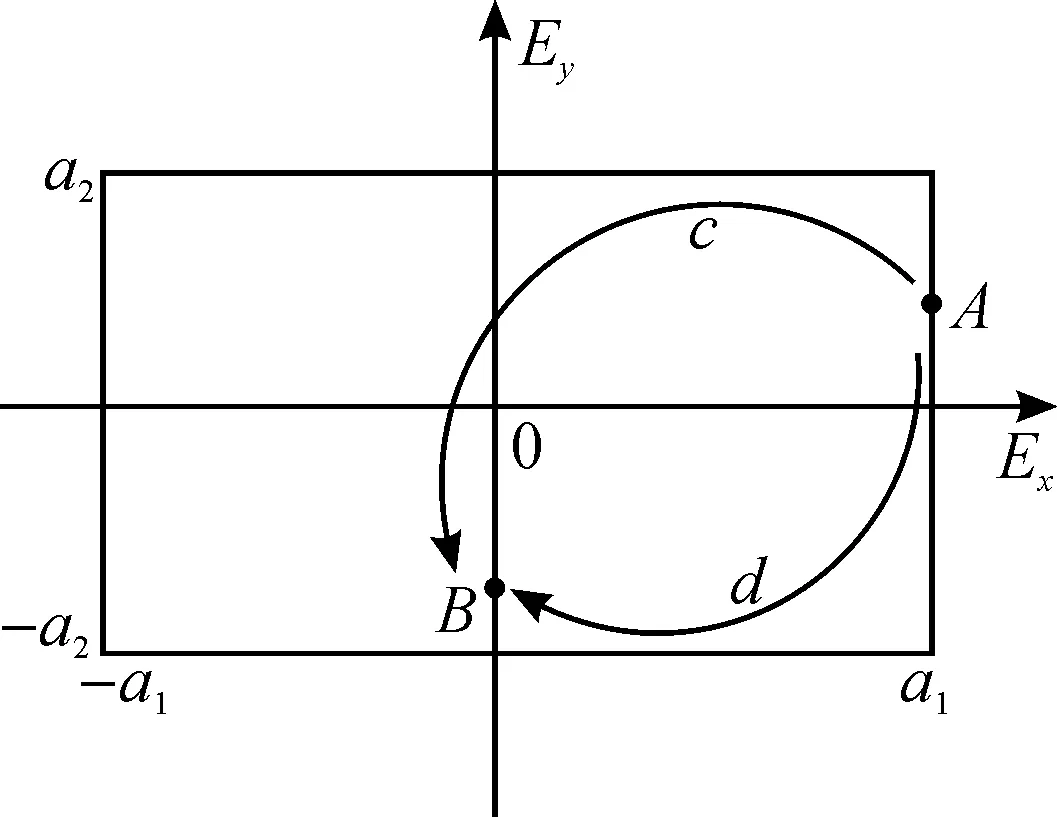
图1 Δφ=π/3时的旋转路径Fig.1 The rotation path of elliptical polarizedlight when Δφ=π/3

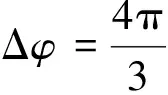
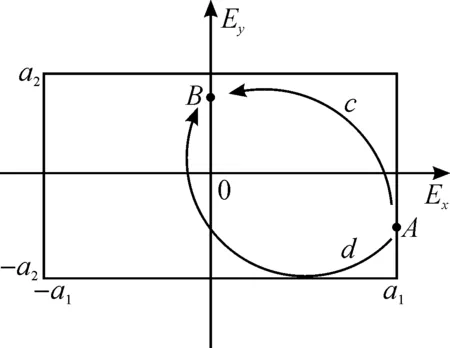
图2 Δφ=4π/3时的旋转路径Fig.2 The rotation path of elliptical polarizedlight when Δφ=4π/3

相位差Δφ为其他值时同理可证.

整理可得：当sin Δφ>0时，为右旋偏振光；当sin Δφ<0时，为左旋偏振光.

3 椭圆偏振光的琼斯矢量表示

3.1 椭圆偏振光的琼斯矢量

光的偏振态可以用琼斯矢量表示. 按第1节中的推导和总结，光在与传播方向(z方向)垂直的xoy平面上的x和y方向上的分量为：

Ex=a1e-i(ωt-kz+φ0x)=a1e-iφx，

(10a)

Ey=a2e-i(ωt-kz+φ0y)=a2e-iφy.

(10b)

用偏振光矢量2个分量构成的一列矩阵表示光的偏振态，称为琼斯矢量，记作

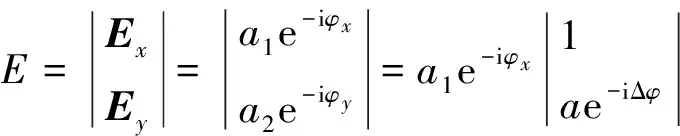
(11)

其中，a=a2/a1，Δφ=φy-φx.

以长轴沿x轴，长短轴之比为2:1的右旋偏振光为例，Δφ=φy-φx=π/2归一化的琼斯矢量为

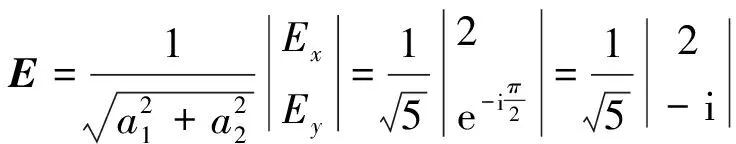
(12)

3.2 各教材琼斯矢量形式的对比分析

各教材中，椭圆偏振光琼斯矢量的最终形式是一致的. 以圆偏振光为例，左、右旋圆偏振光的琼斯矢量分别为：

(13)

各版本在推导中，给出的说明均不够清晰，有的甚至前后矛盾. 以姚启钧的《光学教程》为例，与式(11)对应的表达式为[5]：

(14)

矩阵第2行为aeiΔφ，Δφ仍是(φy-φx)，与本文式(11)的指数部分差一个负号. 但式(14)左右并不相等. 通过简单指数运算发现，式(11)才是正确的. 而且《光学教程》[5]中对右旋圆偏振光的琼斯矢量是这样描述的：

(15)

4 总 结

鉴于各版本光学教材对于光的波函数表达式、椭圆偏振光的旋向判断、偏振光的琼斯矢量等知识点的表述存在差异，甚至互相矛盾，为厘清思路，明确结论，帮助学生扫清学习障碍，对以上3个知识点进行了较透彻的分析. 通过从头推导平面简谐电磁波的波函数，给出了几种表达形式，认为各版本虽然形式不尽相同，但运算结论是一致的；通过证明椭圆偏振光旋向与两子波相位差的关系，得到当sinΔφ>0时，为右旋偏振光；当sinΔφ<0时，为左旋偏振光的结论；通过细致的推导，给出了偏振光琼斯矢量的正确表达式，同时指出，文献[5]对偏振光的琼斯矢量描述存在前后不一致的问题.

本文有助于学生厘清思路，扫清学习障碍，更好地学习掌握椭圆偏振光这一知识点，也可为相关老师提供教学案例和参考.

[1] 玻恩M，沃耳夫E.光学原理(上册)[M].北京:北京大学出版社,1985:29-52. BORN M, WOLF E. Principles of Optics (Vol one)[M]. Beijing：Beijing University Press,1985:29-52.

[2] 叶玉堂，肖峻，饶建珍，等.光学教程[M].北京:清华大学出版社,2011:117-132，299-303. YE Y T, XIAO J, RAO J Z，et al. Optics Tutorial[M]. Beijing：Tinghua University Press,2011:117-132，299-303.

[3] 赵凯华，钟锡华.光学[M].北京:北京大学出版社,1984:140-147，187-199. ZHAO K H, ZHONG X H. The Optics[M]. Beijing：Beijing University Press,1984:140-147,187-199.

[4] 郁道银，谈恒英.工程光学[M].北京:机械工业出版社,2013:291-295,327-329,494-495. YU D Y, TAN H Y. Engineering Optics[M]. Beijing：China Machine Press, 2013:291-295,327-329,494-495.

[5] 姚启钧.光学教程[M].北京:高等教育出版社,2002:19-78,336-365. YAO Q J. Optics Tutorial[M]. Beijing：Higher Education Press,2002:19-78,336-365.

YANG Jing, LI Shaofeng, ZHANG Lihong, ZHU Xinying, WANG Hankui

(ThePhysicsandTelecommunicationEngineeringCollege,ZhoukouNormalUniversity,Zhoukou466000,HenanProvince,China)

In the widely used optics textbooks for undergraduate students, the following conclusions and their derivation process are inconsistent, and even contradictory: (1)The wave function expression of the planar harmonic electromagnetic wave; (2)The relationship between the rotation direction of elliptically polarized light and the phase difference of two sub-waves; (3)The derivation and form of Jones vector of elliptically polarized light. These inconsistencies often make students confusing. Based on years of teaching experience in optics, we conduct a comparative analysis for these inconsistencies by proof and derivation, and draw clear conclusions for each of the above knowledge.

wave function; elliptically polarized light; rotation direction; Jones vector

2016-06-08.

国家自然科学基金资助项目(11547227);河南省教育厅教师教育课程改革研究项目(2016-JSJYYB-096);周口师范学院高层次人才科研启动项目(ZKNU2014121).

杨 静(1986-)，ORCID:http://orcid.org/0000-0002-2823-949X，女，博士，讲师，主要从事气体激光物理研究，E-mail:yangjing0410@zju.edu.cn.

10.3785/j.issn.1008-9497.2017.01.008

O 436.3

A

1008-9497(2017)01-053-04