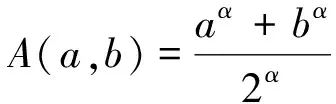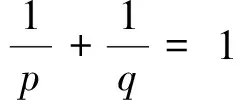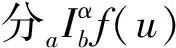分形集上广义凸函数的新Hermite-Hadamard型不等式及其应用
孙文兵,刘 琼
(邵阳学院 理学与信息科学系, 湖南 邵阳 422000)
分形集上广义凸函数的新Hermite-Hadamard型不等式及其应用
孙文兵,刘 琼
(邵阳学院 理学与信息科学系, 湖南 邵阳 422000)
基于局部分数阶微积分理论,利用分形集上广义凸函数的定义,对Hermite-Hadamard型不等式进行一些有意义的推广,得到了几个分形集Rα(0<α≤1)上涉及局部分数积分的新Hadamard型不等式. 最后, 给出了其在特殊均值和数值积分中的几个应用.
Hadamard型不等式; 广义凸函数; 局部分数积分; 局部分数阶导数; 分形空间
New inequalities of Hermite-Hadamard type for generalized convex functions on fractal sets and its applications. Journal of Zhejiang University(Science Edition), 2017,44(1):047-052
函数凸性是数学分析中的一个重要定义,很多重要的数学不等式是建立在函数凸性定义之上的,比如著名的Hermite-Hadamard不等式.
设f:I⊆R→R是一个凸函数,若a,b∈I且a (1) 这就是著名的Hermite-Hadamard不等式.随着凸性定义的推广,Hermite-Hadamard不等式也受到国内外越来越多学者的关注[1-6]. 由于分形理论的出现,物理和工程等领域的许多问题方得以合理处理和解决.近年来,随着分形理论在科学工程领域的广泛应用,数学作为重要的研究工具发展迅速.一些学者通过不同的方法构建了分形空间上的微积分理论[7-10].文献[9]系统阐述了建立在分形空间上的局部分数阶微积分的相关理论.文献[11]提出了关于分形集上广义凸函数的定义,研究了广义凸函数的相关性质,并证明了分形集上的广义Hermite-Hadamard不等式: (2) 受文献[7-11]的启发,本文基于文献[9]构建的局部分数阶微积分理论,引入文献[11]关于分形集上广义凸函数的定义,对Hermite- Hadamard型不等式进行一些有意义的推广,证明Hermite-Hadamard型不等式在分形空间中的几个变式,最后提出这些不等式在求特殊均值以及求局部分数阶积分上的应用. 设Rα为分形空间上的实数集,利用GAO-YANG- KANG的方法给出局部分数阶导数和局部分数阶积分的定义,参见文献[9-10]. 若aα,bα,cα∈Rα(0<α≤1),则 (1)aα+bα∈Rα, aαbα∈Rα, (2)aα+bα=bα+aα=(a+b)α=(b+a)α, (3)aα+(bα+cα)=(a+b)α+cα, (4)aαbα=bαaα=(ab)α=(ba)α, (5)aα(bαcα)=(aαbα)cα, (6)aα(bα+cα)=aαbα+aαcα, (7)aα+0α=0α+aα=aα, 且aα1α=1αaα=aα. 下面给出分形集Rα上局部分数阶导数和局部分数阶积分的定义. 定义1[9]设f:R→Rα,x→f(x)是一个不可微函数,如果对于任意的ε>0,总存在δ>0,其中ε,δ∈R,使得当|x-x0|<δ时有 |f(x)-f(x0)|<εα,则称不可微函数f在x0处局部分数阶连续.f(x)在区间(a,b)上局部分数阶连续,记为f(x)∈Cα(a,b). 定义2[9]若 定义3[9]设 则称之为f(x)的α阶局部分数阶积分. 定义4[11]设f:I⊆R→Rα,对任意x1,x2∈I且λ∈[0,1],如果以下不等式成立: f(λx1+(1-λ)x2)≤λαf(x1)+(1-λ)αf(x2), 则称f为定义在I上的广义凸函数. 引理1[9](1)设f(x)=g(α)(x)∈Cα[a,b],则 (2)设f(x),g(x)∈Dα[a,b],且f(α)(x),g(α)(x)∈Cα[a,b],则 (3) (4) (5) (6) (7) 将式(4)(5)(6)(7)相加,并由第1节中分形空间Rα上的运算性质第(2)条,可知结论成立. 利用引理4,可以得到以下结论: (8) (9) 由引理2,可知 (10) (11) (12) (13) 并且 (14) 定理得证. (15) 由定理1的式(8)可得结论成立. 推论2 在推论1的结论中取x=a,可得 (16) (17) (18) 同理可得 (19) (20) (21) 根据定理1的证明,将式(10)和式(18)~(21)代入式(9),可得不等式(17),定理得证. 3.1 在特殊均值中的应用 考虑如下广义均值: n∈Z{-1,0},a,b∈R,a≠b. (22) 证明 在推论2中,取 f(x)=xnα,x∈R,n∈Z,n≥2,则 结论得证. 3.2 在求积分中的应用 下面考虑前面涉及局部分数积分的不等式在局部分数积分的求积方法中的应用. 考虑区间[a,b](0 (23) 定义逼近积分的梯形公式 命题2 设I⊆R是一个区间,f:Io⊆R→Rα(Io是I的内部)使得f∈Dα(Io)且f(α)∈Cα[a,b],其中a,b∈Io,a (24) 证明 由推论2,在分划In的每一个子区间[xi,xi+1](i=0,1,…,n-1)上,有 对i从0到n-1对上式两边求和,由三角不等式得 [1] LATIF M A. Inequalities of Hermite-Hadamard type for functions whose derivatives in absolute value are convex with applications[J]. Arab J Math Sci, 2015,21(1): 84-97. [2] ALOMARI M W, DARUS M, KIRMACI U S. Some inequalities of Hermite-Hadamard type for s-convex functions[J]. Acta Mathematica Scientia:Ser B,2011,31(4):1643-1652. [3] BAKULA M K, ÖZDEMIR M E, PECARI J E. Hadamard-type-inequalities form-convex and (α,m)-convex functions[J]. Hrvatska Znanstvena Bibliografija I MZOS-Svibor, 2012,59(1):117-123. [4] LATIF M, SHOAIB M. Hermite-Hadamard type integral inequalities for differentiable m-preinvex and (α,m)-preinvex functions[J]. Journal of the Egyptian Mathematical Society, 2015, 23:236-241.[5] OZDEMIR M E, AVCI M, KAVURMACI H. Hermite-Hadamard type inequalities via (α,m)-convexity[J]. Comput Math Appl, 2011, 61: 2614-2620. [6] OZDEMIR M E, YILDIZ C, AKDEMIR A O, et al. On some inequalities fors-convex functions and applications[J]. Journal of Inequalities and Applications, 2013, 333:1-11. [7] BABAKHANI A, DAFTARDAR-GEIJI V. On calculus of local fractional derivatives[J]. J Math Anal Appl,2002,270(1):66-79. [8] ZHAO Y, CHENG D F, YANG X J. Approximation solutions for local fractional Schrodinger equation in the one-dimensional Cantorian system[J]. Adv Math Phys,2013:1-5. Article ID291386. [9] YANG X J. Advanced Local Fractional Calculus and Its Applications[M]. New York: World Science Publisher, 2012. [10] YANG Y J, BALEANU D, YANG X J. Analysis of fractal wave equations by local fractional Fourier series method[J]. Adv Math Phys,2013,2013:377-384.Article ID632309. [11] MO H X, SUI X, YU D Y. Generalized convex functions on fractal sets and two related inequalities[J]. Abstract and Applied Analysis,2014,2014(1):1-7. Article ID636751. SUN Wenbing, LIU Qiong (DepartmentofScienceandInformationScience,ShaoyangUniversity,Shaoyang422000,HunanProvince,China) On the basis of local fractional calculus theory, inequalities of Hermite-Hadamard type are extended following the definition of generalized convex function on fractal sets. Some new Hadamard-type inequalities involving local fractional integrals on fractal setsRα(0<α≤1) are established. Finally, some applications of the new inequalities in special means and numerical integration are provided. Hadamard-type inequalities; generalized convex function; local fractional integral; local fractional derivative; fractal space 2016-03-22. 邵阳市科技计划项目(2015NC43);湖南省自然科学基金资助项目(12JJ3008). 孙文兵(1978-),ORCID:http://orcid.org/0000-0002-5673-4519,男,硕士,讲师,主要从事解析不等式、智能算法研究,E-mail:swb0520@163.com. 10.3785/j.issn.1008-9497.2017.01.007 O 178 A 1008-9497(2017)01-047-06


1 预备知识



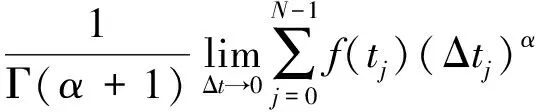
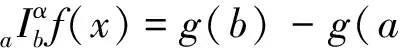
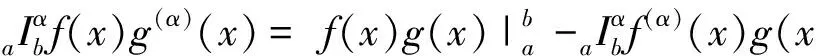




2 主要结果和证明


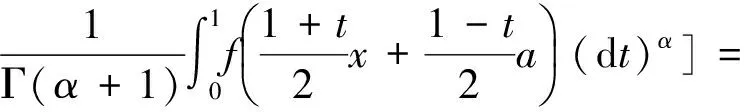





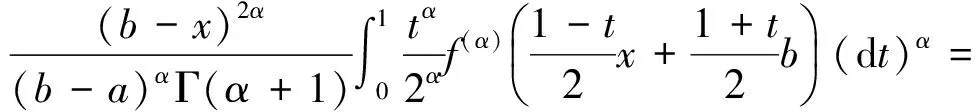





























3 应用举例