运用假设 化难为易

涂静秀

(江苏省苏州市吴江中学 215200)

假设法是对所解的问题，在不违背原题的前提下，人为地加减某些条件，为解决物理难题找到了新的路径，一定程度上有利于化解疑难问题.假设法的运用打破了解决物理难题的常规方法.本文探究了假设法的几种应用，希望能帮助学生提升解题能力.

一、判断液体的移动

判断液面的移动是一种常见的物理题型，由于某些物理量的循环变化、不易确定，提升了这类问题的解题难度，而使用假设法就可以很好的解决这些问题，而且使用假设法处理此类问题往往可以收到意想不到的效果.

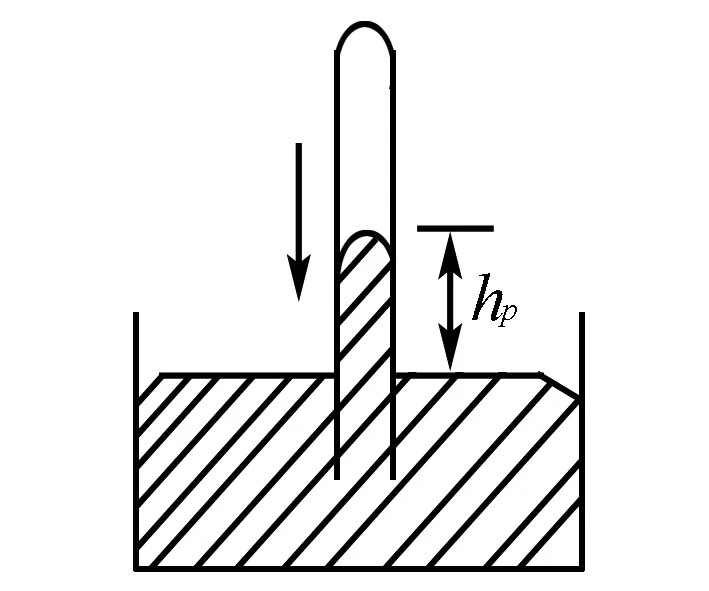
图1

例1 如图1所示，一开口朝下的玻璃管插入水银中，管内的水银面比管外的高出hm，管的顶端封闭有一定质量的空气.现将玻璃管竖直向下再插入水银面一些，则h将( ).

A.变小 B.不变

C.变大 D.无法判断

解析用假设法分析可知：h的变化有三种情况：变小、不变、变大.首先我们假设h不变，则管内气体压强p=p0-h不变，管竖直向下插入，管内体积将减小，由玻意耳定律可知，管内气体压强应增大，这与假设矛盾，即h改变.

然后我们假设h变大，根据p=p0-h可知p减小，管竖直向下插入，气体体积将明显减小，由玻意耳定律可知，管内气体压强p增大，这与假设再次矛盾.综上可知，h变小，p增大，V必减小.A正确.

点评本题若用常规的方法求解，较难突破局限，因为气体的压强不易确定.但用假设法分析h的三种变化可能，将问题化繁为简，绕过难点，然后根据玻意耳定律进行分析，解决问题．

二、引用力矩平衡

阿基米德说：“给我一个支点我能翘起整个地球”是基于对力矩的应用，当力与力的中心作用点有一定距离的时候就会产生力矩，利用假设法找到中心作用点，接着就可以应用力矩平衡，从而解决问题.

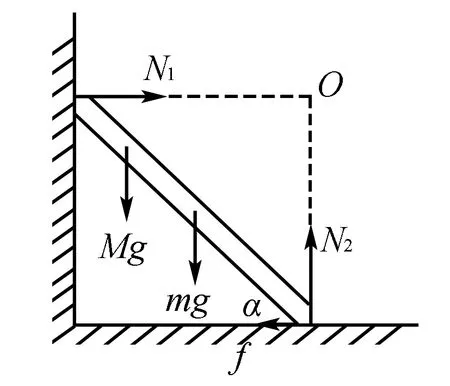
图2

例2 如图2所示，一条质量为m，长为L的梯子，上端靠在光滑竖直墙上，下端抵在粗糙水平地面上，与地面成α角.质量为M的人站在距离梯子上端l处，求阻止梯子滑动的地面摩擦力的大小.

解析依据题干，将梯子作为

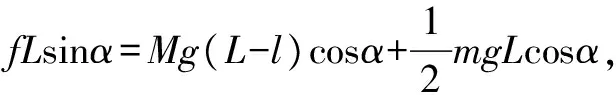
点评本题以梯子为研究对象，由于N1、N2和f均未知，若要根据共点力和力矩平衡条件求解f，过程比较繁琐.若利用假设法扩大视野找到中心作用点O，从而使整体解题思路比较明快，难度中等.

三、进行受力分析

受力分析一般具有很强的综合性和复杂性，假设法是一种思维方法，灵活运用假设法，往往可使问题变不可能为可能，使得解题思路变得清晰，让所求问题迎刃而解，现就常用的假设法对受力分析进行说明.

例3 已知有三个半径为r、质量为m的球放在一个半球形碗中，现将第4个一模一样的球放在这三个球的正上方，放入碗中，并要求四个球都静止.碗内非常光滑，可忽视摩擦力，请问半球形碗的半径是多少？

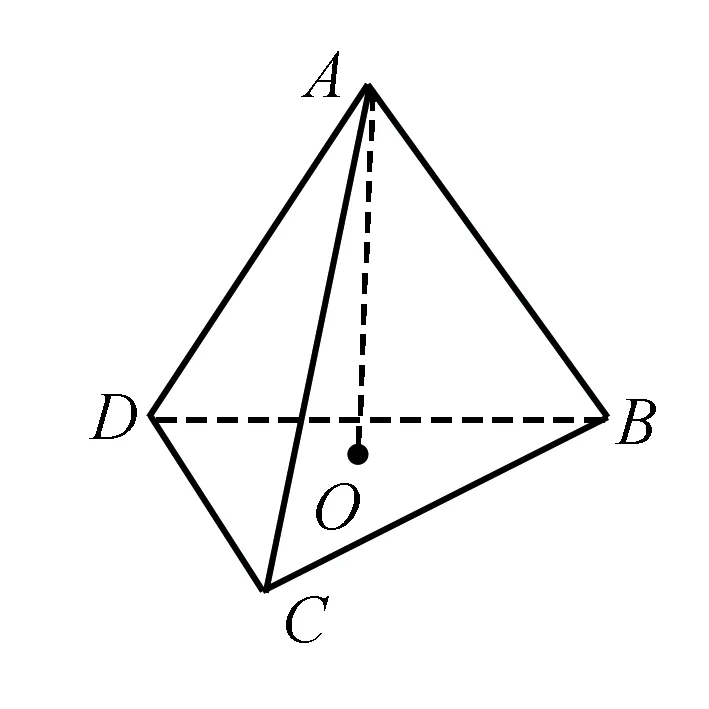
图3

解析由题可知，假设碗的球面半径很大，把碗面看作平面.由于，忽视摩擦力，所以当放上第4个球体的时候，下面的三个球会出现散开的现象.故临界情况是放上第4个球后，其它三个球之间刚好无弹力.假设把第四个球记为A，下面三个球依次为B、C、D，则四个球的球心连起来就会构成一个如图3所示边长为 2r的正四面体.

设A、B球心的连线与竖直方向的夹角为α，设碗面球心为O，O与B球心的连线与竖直方向的夹角为β，碗面对上面三个球的弹力都为F，如图4所示.

当以整体为研究对象时，受力分析得，在竖直方向上有3Fcosβ=4mg①，

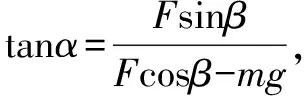
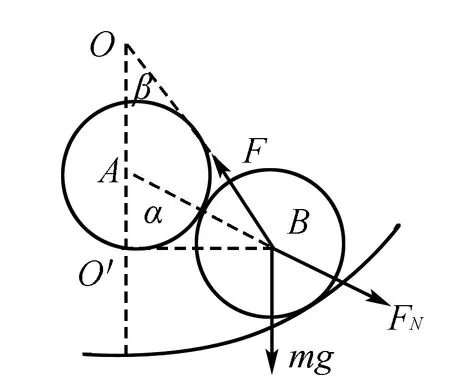
图4

点评本题在受力分析的问题上，我们假设碗的球面半径很大，把碗面变成平面．假设出了一种物理想象和创造过程，突破思维障碍，再结合共点力平衡，模型几何关系，使所求问题迎刃而解.

四、转换动静关系

对于运动的物体，一般可以作为质点考虑，但是对于一些体积比较庞大的物体，比如火车之类，再将其当作质点考虑就会导致物理情景模糊，使得问题难以解决.此时不妨采用假设法法，转换两者之间的动静关系，以运动的物体作为参照物，往往会使得难以解决的问题变得柳暗花明.

例4 高铁从静止到最大速度是一个匀加速过程，现在通过测量发现高铁的车头和车尾通过某个路标的速度分别为10m/s和20m/s，请求出高铁列车的中点通过路标时的速度.

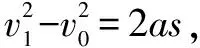
点拨本题的解法打破思维定势，采用逆向思考，将运动的物体和静止的物体进行转换，让原本无法解决的问题变得柳暗花明，将本题中的路标作为质点考虑，不会导致物理情景模糊，可以说本题的解法非常具有创造力.

综上所述，假设法可以将复杂问题简单化，抽象问题具体化，是解决物理问题时不可多得的好方法.但是学贵得法，在学习的过程中不光要学习理论知识，还要学会归纳和总结，建立属于自己的知识体系，同时掌握一定的解题方法，这样才能学以致用，在解题是做到有的放矢.

[1]张新民.用极端假设法分析物理难题例谈[J].高考(综合版).2015(06).

[2]孙中军.浅论高中物理中常用的几种解题方法[J].中国校外教育.2016(04).