结合判别式，巧解数学题

朱秋萍

(江苏省如皋市第二中学 226500)

一、不等式证明

判别式在高中数学中占有非常重要的地位，它是等式与不等式相联系的重要桥梁，巧用判别式简解数学题的思路是，从条件出发等价转化构造出关于某个变量的一元二次方程或一元二次不等式或一元二次函数，进而通过判别式简解问题.

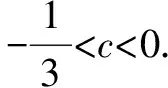
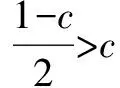
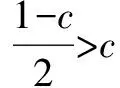
点拨本题巧用判别式简解数学题的思路是，将c看成常量，观察a、b之间的关系利用韦达定理构造出一元二次方程，将c代入方程，得到关于c的一元二次方程，利用判别式法，结合题目中的条件解答问题.

二、求解三角函数中角的值

巧用判别式简解三角函数中的角值，关键在于构造出关于某个变量的一元二次方程，再根据方程根的个数，然后利用判别式与0的大小，构造出三角函数中的角的取值范围，得出三角函数中角的值.

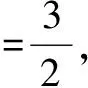
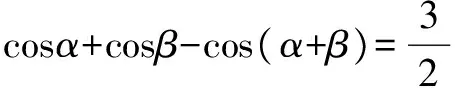
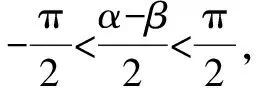
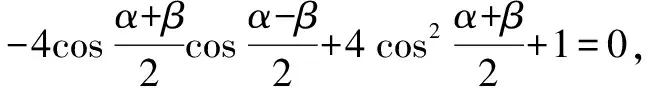
三、解平面几何问题

将一元二次方程根的判别式应用于几何，应注意根据几何图形的性质，构造关于某一几何量为元的一元二次方程，判别式法常可以避免许多复杂的数学运算，而且几何意义清晰，不失为一个方便、有效的好方法.

例3 三角形ABC中，已知AB=c及其相对的C角，求内切圆半径r的取值范围.

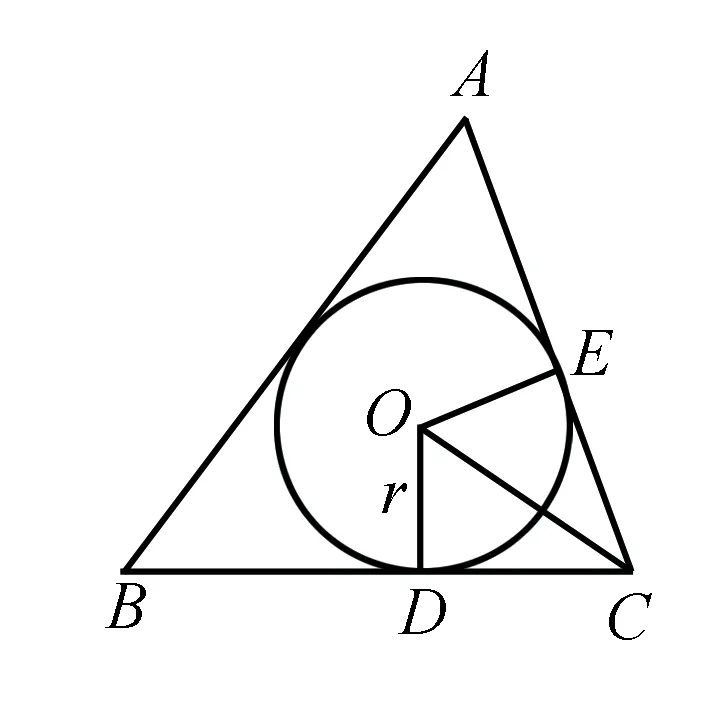
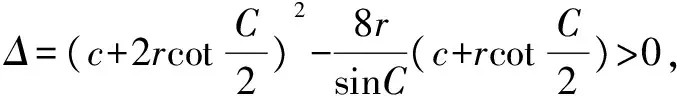
又r>0，

点拨本题求解内切圆半径r的取值范围的过程中，根据三角形的性质，得到a、b之间的关系，利用韦达定理得到一元二次方程，再利用Δ>0，使问题变得轻巧简捷，因此判别式法在几何问题中也能够得到广泛的应用.

四、求解极值

二次函数的判别式也常常应用与极值的求解，通过将原来的函数进行转化，得到一元二次方程的一般形式，从而根据判别式求出系数的极值，此种方法的关键在于“降次”，通过下面的例题可以对判别式求极值有一个基本的了解.

例4 若实数a，b，c满足a+b+c=0，a2+b2+c2=1，则a的最大值为____.

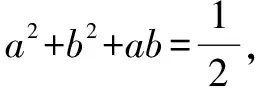
点拨本题的关键在于消元，首先将“三元”转化为“二元”，接着又将“二元”转化为“一元”，最终将问题转化为一元函数的最值问题，通过巧妙的转化，利用一元二次方程根的判别式，巧妙地求出了a的极值.

综上所述，对有些看似与一元二次方程毫无关联的数学问题，可以通过等价转化构造出一元二次方程，进而利用判别式能使问题由繁化简，最终巧妙地解决数学问题.希望学生们在以后的解题过程中，能够学会使用判别式，来解一元二次方程以外的问题.

[1]张丽萍.巧用判别式求函数的最值[J].高中数理化,2011(23).

[2]王云峰.判别式法[J].数学教学通讯,2011(07).