常见高考热点题型
——数列求和方法归类
张瑞琦
(安徽省明光市第三中学 239400)
数列作为高中数学的学习中很重要的一个环节,经常和函数,不等式,方程,微积分,极限方面结合形成比较综合的题目,而且也经常涉及到分类讨论和等价转换等重要的思想方法和数学基本技能.在每年的高考中有关数列问题都是必考的考点,也是重点.数列求和问题是一个技巧性强,灵活度大,方法多的模块,高考若要取得好分数,学好数列是必须的.本文对高中阶段一般数列的求和方法进行了归纳和总结.
一、公式法

思路分析直接用公式求和.
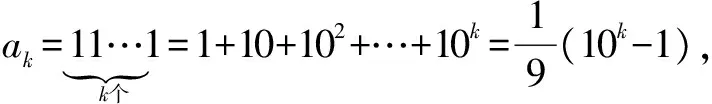
二、分组求和法
分组求和法就是将数列的项分成二组,而这两组往往是常数或是等差(比)数列,进而利用等差数列或等比数列的求和方法分别求和,然后再合并,从而得到该数列的和.

将其每一项拆开再重新组合得
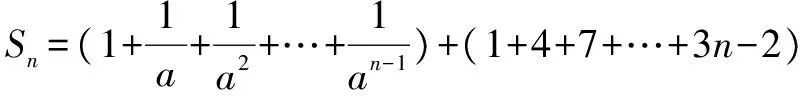

当a≠1时,
三、裂项相消法
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的.
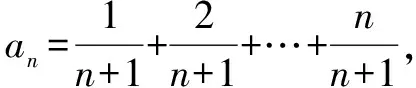
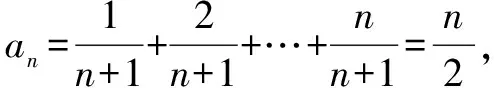
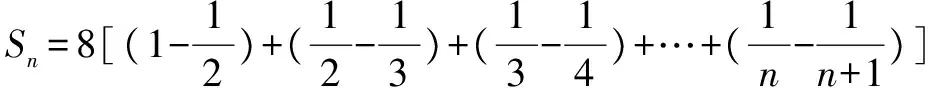
四、错位相减法
这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an·bn}的前n项和,其中{an}、{bn}分别是等差数列和等比数列.
例4 已知数列{bn}(n∈N*)是递增的等比数列,且b1+b3=5,b1b3=4.
若数列{an}的通项公式是an=n+2,数列{anbn}的前n项和为Sn,求Sn.
解anbn=(n+2)·2n-1,所以
Sn=3·20+4·21+5·22+…+(n+2)·2n-1,
2Sn=3·21+4·22+5·23+…+(n+2)·2n.
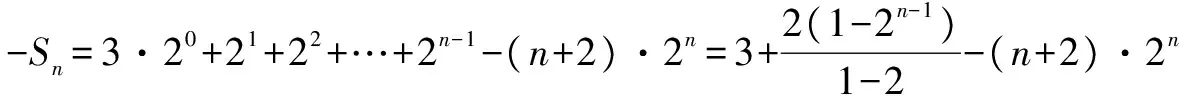
所以Sn=(n+1)·2n-1.
五、倒序相加法
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1+an).
例5 求sin21°+sin22°+sin23°+…+sin288°+sin289°的值.
解设S=sin21°+sin22°+sin23°+…+sin288°+sin289°①,
将①式右边反序得S=sin289°+sin288°+…+sin23°+sin22°+sin21°②.
又因为 sinx=cos(90°-x),sin2x+cos2x=1,
得2S=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin289°+cos289°)=89,
∴S=44.5.
六、猜想归纳法
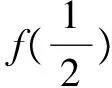
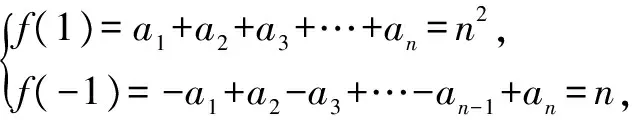


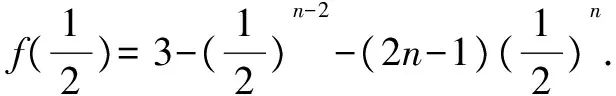
七、极限求和
当数列为无穷数列,这就是我们高等数学要学的一个重要组成部分——级数,那它的和怎么求呢?下例是分子,分母由多项式组成的分式的极限,这类问题往往与数列求和、求积相联系,一般应先对极限式子变形,再运用极限法则求极限.
例7 计算:
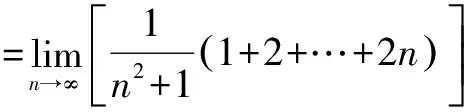
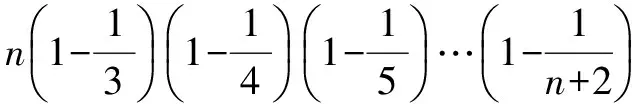
上文提到的几种类型是我们在高中阶段最常见的几种基本类型,在做题的时候要根据题目的具体特征选择合适的方法转化为这几种简单的形式求解.数列作为初等数学和高等数学之间的衔接点与函数,方程还有不等式之间都有着很紧密的联系,所以这类问题自然就成为高考中的热点内容.对于数列这类问题,本文只是做了一点简要的归纳,希望对同学们的高考复习备战有所帮助.
[1] 叶锋.浅谈数列的求和[M].成都:成都教育出版社,2006.
[2] 广冬雁,李居强,刘利琴.数列求和十法[J].数理化学习(高中版),2002(18).
——由倒序相加想到倒序相乘

