例谈数列中参数范围问题的多种解题方法

祝忠虎

(甘肃省永昌县第一高级中学 737200)

近年来,各省高考试题及高考模拟试题中出现了颇有新意、构思精巧的数列不等式恒成立求参数范围的综合题，这类题涉及知识面广、综合性强，对能力要求较高，能较好地考查学生的思维能力，很值得重视和探究.下面举例说明此类问题的解题策略，供参考.

一、分离参数法

例1 已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.

(1)求数列{an}的通项公式；(2)设数列{an}的前n项和为Sn，若不等式Sn>kan-2对一切n∈N*恒成立，求实数k的取值范围.

解 (1)略.

所以，不等式3(2n-1)>k·3·2n-1-2,即k<2-

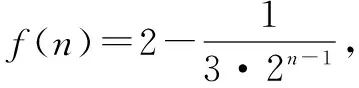
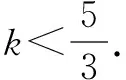
点评 对于参数与主变量未分开的不等式恒成立问题优先考虑分离参数再转化为最值问题处理.

二、单调性法

点评 对于与数列单调性有关的不等式恒成立问题可以利用数列单调性定义转化为不等式恒成立问题的一般形式再求参数范围.

三、最值(有界性)法

(Ⅰ)求数列{bn}的通项公式；

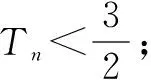
(Ⅲ)设数列{bn}的前n项和为Rn,已知正实数λ满足：对任意正整数n,Rn≤λn恒成立，求λ的最小值.

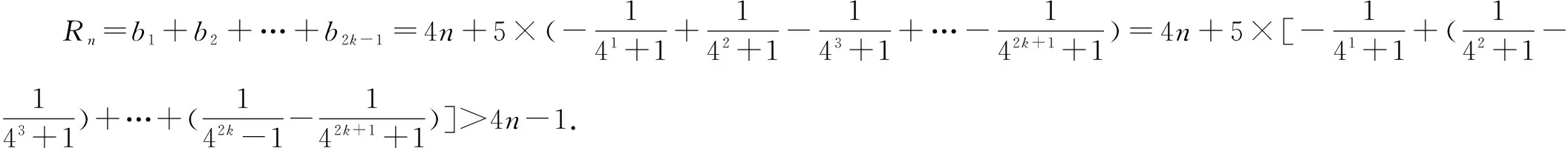
∴λn≥Rn>4n-1,即(λ-4)n>-1对一切大于1的奇数n恒成立.

另一方面，当λ=4时，对一切的正整数n都有Rn≤4n.

事实上，对任意的正整数k，有

∴当n为偶数时，设n=2m(m∈N*),

则Rn=(b1+b2)+(b3+b4)+…+(b2m-1+b2n)<8m=4n.

当n为奇数时，设n=2m-1(m∈N*),

则Rn=(b1+b2)+(b3+b4)+…+(b2m-3+b2m-2)+b2m-1<8(m-1)+4=8m-4=4n.

∴对一切的正整数n，都有Rn≤4n.

综上所述，正实数λ的最小值为4

点评 对于一边能求和(或放缩后能求和)的数列不等式恒成立问题，一般先求和再求出数列和的最值(或上界、下界)，进而求出参数范围.

[1]彭浪.试析高中数学概念的教学方法[J].中学生数理化(教与学),2016(01):78-79.

[2]刘兆强.浅谈高中数学概念的教学方法[J].青春岁月,2016(13):149.

[3]苏振新.高中数学概念的教学方法研究[J].黑河学刊,2014(12):95-96.