老师会提问，学生才会学习

陈才丽

摘 要：“师者，所以传道授业解惑者也。”在推进新课程改革、全面实施素质教育的今天，这句话恐怕应该修正一下。老师要做的不是简单的传道授业，而是要使用某些手段和方法，使学生得道、解惑。“提问”是实现这一目标较常规、较有效的方法。课堂提问，对于集中学生的注意力、激活学生的思维、活跃课堂气氛、达成知识的生成和巩固所学的知识以及培养学生的口头表达能力和建立学生的自信心，都起到积极的作用。

关键词：数学教学；提问要求；提问时机

一、提问的要求

提问是一门艺术。笔者认为：首先，所提问题要有内容。教学中有些老师讲述完一个问题后问“听懂了没有啊？”“是不是？对不对？”这样的问题不是问题，所提问题不能过于简单。一连串过于简单的问题抛出去学生都整齐快速地回答，所提问题要有针对性。例如，笔者前不久在讲授“勾股定理”第一课时的时候，提过这样一个问题：“同学们，毕达哥拉斯在一块地板上发现了一条著名的定理，现在我们也看看这幅图，你们能发现什么？”这个看似开放性的问题却没有收到好的效果。有针对性的问题能避免没有价值的发散，切入正题。还有，所提问题要有启发性。遭遇重难点及易错点的时候，学生一下子不能掌握正确的方向，教师此时应给予恰当的提示，让学生“跳一跳，能够到”，使学生的思维得到训练的同时，享受成功的快乐。最后，提问后要注意给学生留下思考的时间。笔者以前就遇到一位老师，把学生想得过高了，提问后没有停留几分钟就急切地问学生“知道了吗？说一说！还没有想到啊！”教育是一个循序渐进的过程，教师不能急于求成，过急容易打击学生的积极性和自信心。

二、提问的时机

1.提问于新旧知识交接处

按照一般的认知规律，新知识大多建立在旧知识的基础上。在新知识讲授之前，教师可以引领学生复习旧知识，抓住新旧知识的联系，在旧知识中找到新知识的生长点。例如：人教版八年级下册16.3分式方程的解法这一课中，在解分式方程=时，我们可以问学生：“以前我们学过解怎样的方程？”“这个分式方程和一元一次方程的区别在哪里？”“可不可以把它转化成解一元一次方程？”“如何达到目的？”“怎样去掉分母？”“比如，=，我们是把等式两边同时乘以6从而达到去分母的目的，那么这个方程呢？”“上例中两边乘以6，6是分母2和3的最小公倍数，这里等式两边乘以的是（20+v）（20-v），它是分母（20+v）和（20-v）的什么呢？”如此学生能够轻松地得出结论——解分式方程的关键和第一步是通过等式两边同时乘以分式的最简公分母，达到去分母从而转化成我们熟知的整式方程。（这里是一元一次方程）

2.提问于众学生的疑惑处

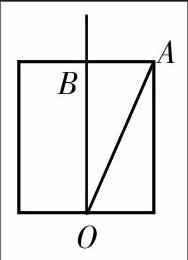
在众多学生遇到疑惑的时候，直接给出答案不是最好的处理方法，因为学生没有经过思考的东西无法内化为自己的内容，被动接受的知识充其量只能在短时间内被记住，或者以一个似懂非懂的印象存在于学生的意识之中。此时还是应该对学生提问，此时的问题更多的应该是启发性的，引导学生一步一步走近答案，最后有学生解决问题。例如，“有一个水池，水面是一个边长为10米的正方形水池，在水池正中央有一根芦苇，它高出水面1米。如果把这个根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面。水的深度和这根芦苇的长度分别是多少？”这道题第一次审题全班有90%的人看不懂题，再次审题还是有50%的人抓不住方向。很多学生认为池深即为10米，芦苇为11米，但是这样理解的话学生自己也觉得不对劲，那题目还问什么呀？正在此疑惑之际，我们可以问：“水深是10米吗？”“那么‘水面是一个边长为10米的正方形水池这句话如何理解？请同学们发挥一下你们的空间想象能力。”“题目给出的图形是一个侧面图，能说出AB是多少吗？BO呢？OA呢？”“BO和OA的关系是什么？”“最后用什么来做？”如此，教师一步一步地抛出问题，学生最后明白题意，而且知道了此题是要运用勾股定理，渗透方程思想的一道题目。

3.提问于同一问题的多解处

你有一个苹果，我有一个苹果，我们交换，每个人还是拥有一个苹果；你有一种方法，我有一种方法，我们交换，每个人就有两种方法。数学课堂中遇到可一题多解的题目时，教师一定不要忘记尽可能地让学生发挥他们各自的聪明才智。此时不妨多问一问：“还有其他方法吗？”“你能为我们阐述一下吗？”这是开拓学生思维的最佳时机，也是培养学生学习兴趣的很好机会。初一下学期学习三角形的时候有一道经典的题目：∠A=20°，∠B=65°，∠C=15°，求∠AOC的度数。学生基本上能说出如下三种作辅助线的方法：前一种利用三角形的内角和为180°，后两个用到三角形的外角。

总之，课堂提问是一种经常使用的教学手段和形式，是教师与学生之间信息的双向交流。教师会提问，能提好问是十分重要的。如果能够在教学中科学地设计并进行课堂提问，就可以及时引起学生的注意，创造积极的课堂气氛，激发学生的学习动机和兴趣，优化课堂结构，真正发挥教师的主导作用和学生的主体作用，从而展示教师的教学艺术，显示教师的教学魅力。