BP神经网络在渔货卸港量预测中的应用

刘航飞，陈昌平，郑艳娜，陈荣庚

（大连海洋大学 海洋与土木工程学院，辽宁 大连 116023）

0 引言

渔货卸港量作为评价港口规划及发展水平的一项主要指标，是渔港建设工程项目规划设计的主要依据。因此进行渔货卸港量的科学预测，对渔港建设工程具有积极的指导意义。目前针对渔货卸港量的预测，各地渔港工程可行性研究报告中普遍采用一元线性回归的时间序列法[1-2]、一元线性灰色理论[3]以及多元线性灰色理论[4]对渔货卸港量进行预测；时间序列法是建立时间与卸货量之间的一元线性回归方程进而对卸港量进行预测，在实测数据较少的情况下，其预测精度较低，误差较大；灰色理论[5-6]则是将原始数列经过累加生成后，建立具有微分、差分近似指数规律兼容的方程，对数据进行预测，但是由于灰色模型本身固有的模型参数少、容错能力差的特点，并且其具有快速衰减和递增的属性，所以它的时效性有限，不适合做长期的预测或分析；然而神经网络[7-8]在研究小样本方面，具有明显的优势；该模型容错能力强、预测和识别速度快以及具有学习和记忆的能力等优点，通过不断的训练和学习，使得预测结果不断的接近实际值；并且其在建模时不需要大量的数据就能得到较好的预测效果，已被广泛应用于经济管理、自然科学、农业科学、工程技术等各个领域。

1 BP神经网络基本原理

人工神经网络具有复杂模式和进行联想、推理记忆的功能，它是解决某些传统方法所无法解决的问题的有力工具。1986年Romelhart和Mc-clelland提出了误差反向传播算法(Error Back Propagation Algorithm，简称 BP算法)，由于多层前馈网络的训练经常采用误差反向传播算法，人们也常把多层前馈网络称为BP网络。该模型具有容错能力强、预测和识别速度快以及具有学习和记忆的能力等优点，因此在模式识别及分类、系统仿真、故障智能诊断、图像处理、函数拟合、最优预测等方面具有广泛的应用。

BP神经网络模型主要由三个部分构成：BP神经网络构建、BP神经网络学习与训练以及BP神经网络的预测，具体的BP神经网络模型流程图如图1所示。

BP神经网络的基本原理为：当网络的输入（即相应影响因素）为时，网络的实际输出为，网络的期望输出（即实际的卸港量）为

定义学习的目标函数为：

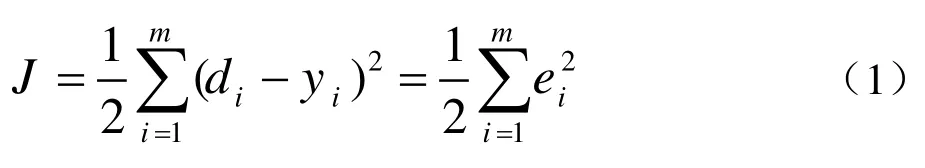
同时 BP算法通过公式（2）来调整权值，使目标函数最小：

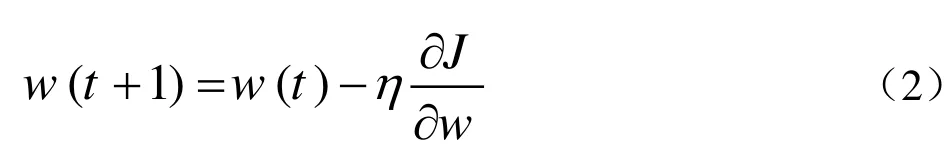
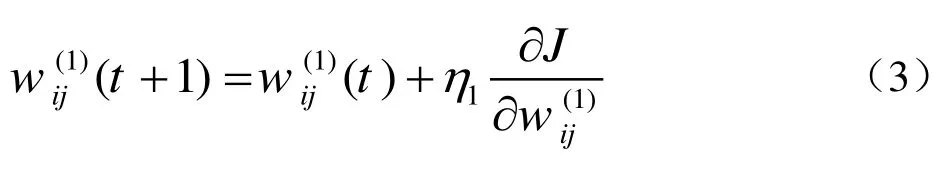
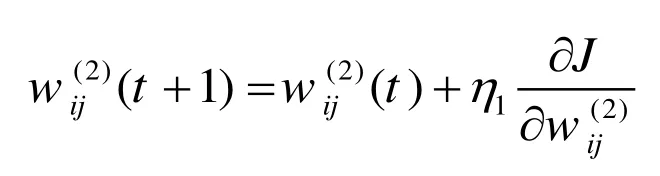
基于以下公式，偏差逐步反传：

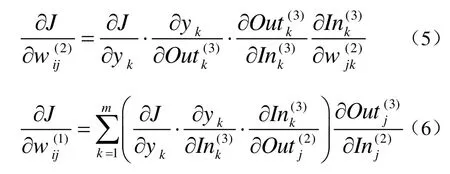
得出各因素的权值后，利用最后处理后的权值对数据进行预测。

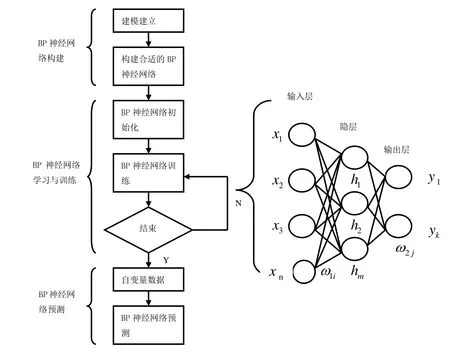
图1 BP神经网络模型运行流程图

2 算例

利用BP神经网络原理，对辽宁省前阳一级渔港1996～2005年的渔货卸港量资料进行训练，然后对2006年的渔货卸港量进行预测。表1为前阳一级渔港1996～2006年实际卸港量。

表1 辽宁省前阳一级渔港1996～2006年卸港量资料

本文中输入层单元个数为1，隐含层单元个数为5，输出层单元个数为1；每次循环100次，期望目标误差最小值 0.001，运用 MATLAB软件编程对辽宁省前阳一级渔港 1996～2005年渔货卸港量样本进行学习和训练。表 2为辽宁省前阳一级渔港1996～2005年实际渔货卸港量和预测渔货卸港量的对比。

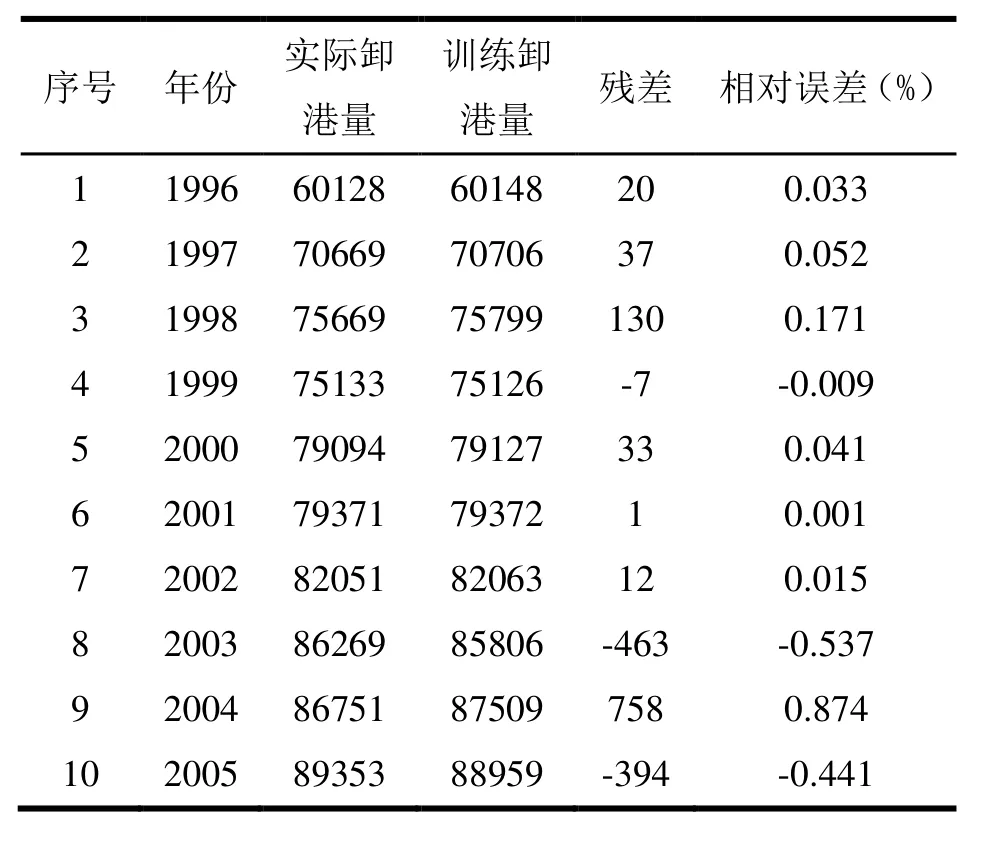
表2 辽宁省前阳一级渔港1996～2005年卸港量BP神经网络预测值与实际值对比表

图2为渔货卸港量的预测值与实际值对比图，由图2可知训练后得到的预测值与实际值更加接近。

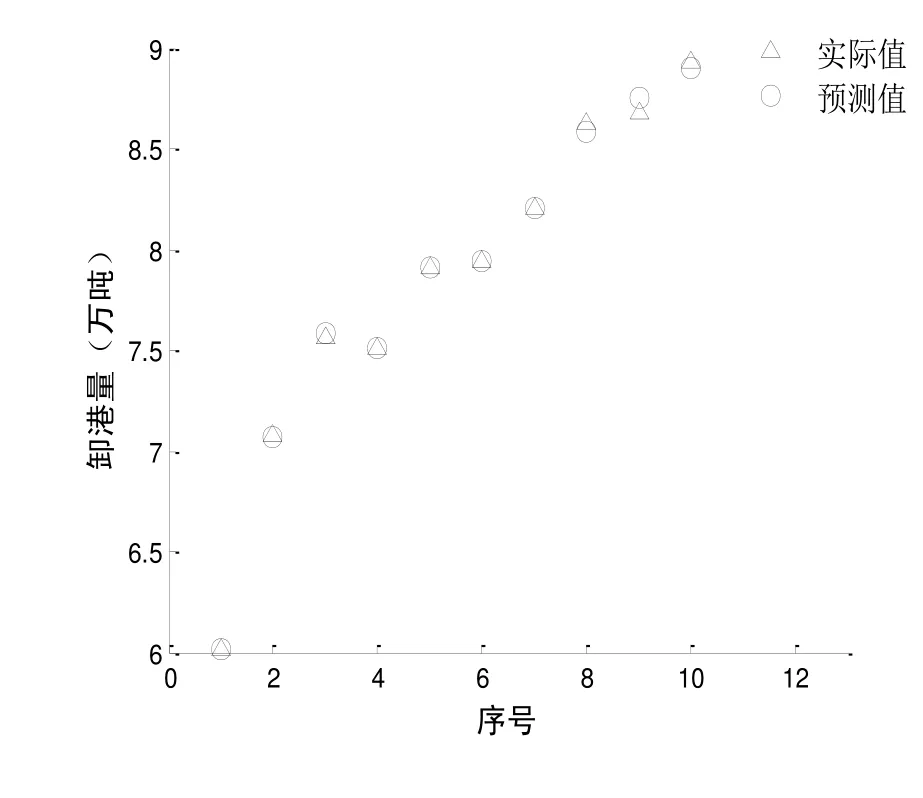
图2 前阳一级渔港实际卸港量和预测卸港量对比图

由表2分析可知，辽宁省前阳一级渔港渔货卸港量每年的相对误差最大值为 0.874%，最小值为0.001%，平均值为0.217%，均小于1%，达到了较高的精度；同样由图2也可以比较直观得出，预测值和实际值非常接近；经过训练后的BP神经网络，其训练得到相关系数R=0.99928，拟合效果非常好；其均方误差MSE趋近于，满足精度要求。

进一步利用 BP神经网络对前阳一级渔港 2006年卸港量进行预测，如表3所示。

表3 卸港量预测结果对比

3 模型应用验证

利用 BP神经网络预测七个渔港渔货的卸港量，并将其与灰色理论以及时间序列的一元线性回归进行比较，如表4所示：

进一步可以得出七个渔港在三种预测方法下的平均相对误差（绝对值的平均值），如表5所示，并对其进行比较。

表5 平均相对误差表

由以上比较可以更加直观得出，BP神经网络模型预测的平均相对误差要小于灰色理论和时间序列法的预测值的平均相对误差，因此采用BP神经网络模型预测具有较好的合理性。

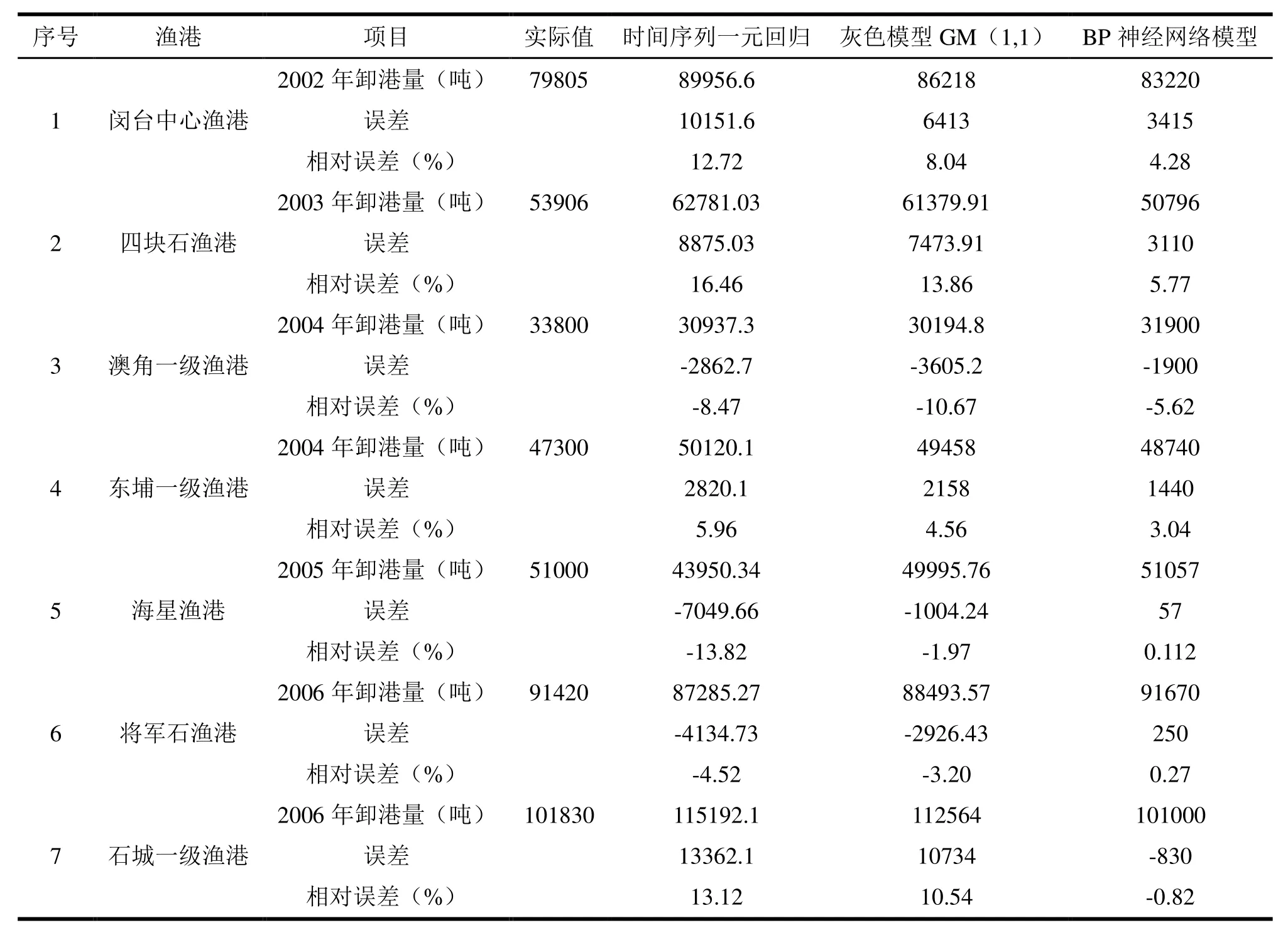
表4 各渔港渔货卸港量预测结果比较

4 结论

BP神经网络预测方法借助MATLAB编程实现，通过不断的学习和训练以及将网络的输出数据与实际数据相比较，直到网络的输出数据对所有训练数据与理想输出数据之差在要求的误差范围之内，从而可以进一步对数据进行预测。通过比较BP神经网络方法、一元线性回归时间序列法和灰色模型GM（1.1）方法的预测结果可知采用BP神经网络方法得到的渔货卸港量预测结果更加接近实际值，精度更高，该模型较低的误差预测结果有利于渔港的前期建设规划工作，便于选取优势渔港进行扩建改造工程，同时准确的渔货卸港量预测对当地渔业产业的发展也有着更深远的实际意义。

[1]桂劲松. 我国渔港卸鱼量发展水平预测方法探讨[J]. 大连水产学院学报, 1995(03): 75-78.

[2]郭子坚. 港口规划与布置[M]. 北京: 人民交通出版社,2011.

[3]周长禄, 王翔宇, 宋忱潞, 等. 灰色模型GM(1,1)在渔货卸港量预测中的应用[J]. 科技创新与应用, 2014(21): 13-14.

[4]陈昌平, 周长禄, 赵学达, 等. 基于灰色多元线性回归方法的渔货卸港量预测[J]. 现代交通, 2014(03): 20-25.

[5]刘思峰. 灰色系统理论的产生与发展[J]. 南京航空航天大学学报, 2004(02): 267-272.

[6]刘思峰, 曾波, 刘解放, 等. GM(1,1)模型的几种基本形式及其适用范围研究[J]. 系统工程与电子技术, 2014(03):501-508.

[7]周政. BP神经网络的发展现状综述[J]. 山西电子技术,2008(02): 90-92.

[8]樊振宇. BP神经网络模型与学习算法[J]. 软件导刊,2011(07): 66-68.