应用基本不等式解题的常用方法分析

孙天贶

（湖南省平江县一中高467班）

应用基本不等式解题的常用方法分析

孙天贶

（湖南省平江县一中高467班）

在高中数学中，基本不等式作为重点知识内容，在实际运用的过程中，需要掌握相应的解题技巧与方法，进而为实现对基本不等式知识的有效掌握奠定了基础，同时，实现对这一知识点的有效掌握，也是学好其他相关知识的基础。通常而言，基本不等式解题的常用方法为：“1”的代换法、换元法、适当拼凑组合法、待定系数法、换元法、消元法以及多次应用不等式法。

一、“1”的代换法

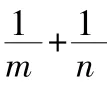
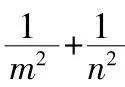
二、换元法的运用

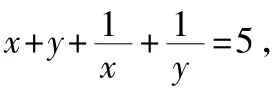
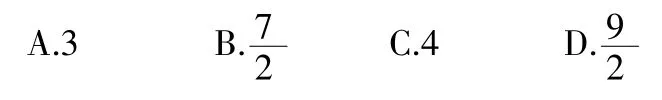
评析：在这一题目中，涉及了x+y与xy，借助基本不等式，可将xy沟通到目标式x+y，通过换元法的运用进行换元，再以解不等式的方式，将x+y的取值范围求出。同样，在相同的条件下，能够求出xy的最大值为4。事实上，在实际解题的过程中，采用换元法的目的是将问题简单化，进而促使不会的问题转变为会的问题，在此基础上，就能轻而易举地得到答案。

三、适当拼凑组合法

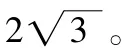
四、待定系数法

例题4：若x2-xy+2y2=4，则3x2+4y2最大值为 （ ）

在实际解析该题目的过程中，则采取待定系数法，在拆分式子运用基本不等式的过程中，最为常见的问题便是如何进行拆分拼借，这也是该方法的重点与难点，在实际进行解决的过程中，则可借助参数，先向目标式方向进行拆分，然后结合最为理想的拆分状态，相应方程列出并进行参数求解，经过这一方法的运用，得出本题的答案为16。

五、消元法

例题5：已知实数x，y满足xy+1=2x+y，且x＞1，则（x+1）（y+1）的最小值为 （）

在实际针对这一题目进行解析的过程中，基于已知条件（x-1）y=2x-1，相应的另外一个条件为x＞1，就能够判断这一题目可借助消元法进行求解，在运用消元法解基本不等式的过程中，需要掌握一定的技巧，或者是借助导数进行求解。

六、多次应用不等式

例题6：正实数a，b满足2a+b=1，则的最小值为（ ）

在针对这一题目进行解析的过程中，可借助多次运用基本不等式的方法，但是需注意的是：等号要满足同时被取到的条件，所以，在第二次运用基本不等式的过程中，则需要将2a+b=1与4a2+之间相互转换，2a+b=1进行平方运算，4a2+4ab+b2=1，设最后问题直接转换为的最小值问题，根据图象求解最小值为

在应用基本不等式解题中，常用的方法较多，在实际进行运用的过程中，需要掌握各种方法的技巧与注意事项，并按照相应的技巧方法按部就班地进行解题，进而能够确保最终得到准确答案。在高中数学中，基本不等式是学习的一大重点知识，同时这一知识点难度也相对较大，因此，在实际学习的过程中，要在把握各种方法所存在规律的基础上，进行多次反复练习，确保能够实现对不同解题方法的熟练运用，为日后相关知识的学习打好基础。

●编辑 鲁翠红