真实脑模型的低频脑节律相位稳定性研究

张吉昌，李红艳

(河北工业大学 电气工程学院,天津 300401)



真实脑模型的低频脑节律相位稳定性研究

张吉昌，李红艳

(河北工业大学 电气工程学院,天津 300401)

对人脑进行三维重建，在此基础上利用偶极子电流模拟低频脑节律源，研究影响低频脑节律相位稳定性的因素.研究发现，脑节律相位稳定性只与节律源的非线性相位波动相关，与脑组织的电导特性、节律源的位置和振幅变动等因素无关.本研究涉及的基于平均相位动态变化的统计方法对同步低频节律的分析和测量有所帮助.

真实脑模型；低频节律；窄带相位稳定性

如今，诸如Delta (0.5～4.0 Hz) 和Theta (4.0～8.0 Hz)等低频脑电图(EEG)脑节律得到了众多学者的关注，这些脑节律与人脑的认知功能及脑生理学和病理学有关[1]，可以从头皮脑电、脑深部脑电或颅内脑电中获得.低频EEG脑节律可以由3个不同的物理参数确定：振幅、频率及初相.理论上，宽带EEG信号可以通过使用基于复杂小波变换(如希尔伯特变换或滤波)的谱分析分解成多段窄带节律信号[2-3].尽管EEG信号宽带相位的一致性已经被研究得很清楚，但其窄带相位动态变化的显著性仍没有被研究透彻.

近几年，通过窄带分析方法观察到的信息流被认为与突触的协调有关，窄带相位熵适合用来对脑区之间功能的连接进行直接评估[4-6].另外，通过对深层脑电的研究，发现癫痫发生过程中的海马区突触重组可能与Theta节律窄带相位的一致性相关.

1 方法

窄带相位一致性(NBPS)能够很好地反映脑节律间同步相位的影响.本研究通过以下步骤来研究NBPS的影响因素：①建立真实的脑皮层模型；②低频脑节律的模拟；③脑节律NBPS的影响因素分析.影响因素包括脑节律的活动、导电媒质的属性及其电导率的变化，这3个因素中任一个因素发生变化时其他的因素应保持不变.

1.1 头部脑皮质模型的三维重建

在两个三维重建模型软件(Simpleware 和Geomagic Studio)的帮助下，脑皮层表面数值模型可以通过256张T1加权核磁图像切片建立，然后使用经典有限元分析计算软件——COMSOL Multiphysics对其进行网格剖分与计算.具体的重建步骤：①建立脑皮层组织的三维模型面.首先，向Simpleware软件中导入大脑的结构磁共振图像(共256张，DICOM 格式，像素矩阵为256×256)，通过设置不同的阈值将脑皮层组织分割出来，应用Simpleware 软件中的填色功能对皮层组织进行优化并保存输出文件.②建立脑皮层组织的数值模型.将保存文件导入Geomagic Studio软件，进行降噪、编辑、过滤等处理，然后运用该软件的边条修整功能清除三维面模型中的空洞和缺陷，最后进行模型特征的提取和片(面)光滑等处理，细化扫描缝隙处的数据，构建脑皮层组织的非均匀有理B样条曲面，如图1(a)所示.③细化后的曲面被导入COMSOL Multiphysics进行网格剖分，共得到35 273个网格，如图1(b)所示.

1.2 低频模拟节律的模拟

一个正弦变化的偶极子电流源被放置在脑模型前半部分(模拟脑额叶部分)的3个位置，在COMSOL软件中的坐标(cm)分别为位置1 (8.2,10.9,5.8)、位置2 (8.2,10.9,6.8)和位置3 (8.2,10.9,7.8).偶极子电流源在模型中的位置如图1(c)所示，位置1为偶极子电流源的默认位置，偶极矩方向为z轴正方向.正弦变化的偶极子电流的振幅分别为0.1 nA(默认值)和0.2 nA，频率为6 Hz，初相分别为0或4t2(t为时间).采样时间窗口为1 050 ms，时间窗口内有134个采样点.脑节律可以由脑模型表面的电场势(FPs)来模拟，图1(d)和图1(e)分别描述了偶极子电流源位于位置1时模型表面的零势面和同电位线.当偶极子电流源活动确定时，FPs可以在COMSOL Multiphysics中求得.由泊松公式的线性化特性可知，不同的偶极子电流初相会使某一确定频率下的模拟节律产生线性或非线性变化，可以研究有着不同初相的偶极子电流对模拟节律NBPS的影响.

图1 脑皮层表面场电势的计算Fig.1 Computation of FPs on the cortical surface

1.3 电导媒质和电导率

1.4 相位稳定性分析方法

实验中，NBPS是通过定义在6 Hz的圆域内的相差进行统计分析的，如公式(1)所示：

(1)

3种统计方法可以用来描述NBPS.

第一，模拟节律在全部剖分网格上所有时间点的相对相位值可以用玫瑰图表示在一个圆内，玫瑰图中花瓣的大小(优选相位数)表示该相位的显著性.相位稳定性(PS)被定义为优选相位数与总相位数的比值[9].很明显，花瓣越大表示模拟节律相位的稳定性越好.

第二，相位稳定性也可表示为模拟节律在采样时间内的平均相对相位值Φ，可以用相位保持指数(PPI)来表示，计算方法如公式(2)所示：

(2)

第三，相位稳定性还可以在EEGLAB中用相位排序的方法进行描述[10].相差通过傅里叶变换或反傅里叶变换被包含在模拟节律中，需要对模拟节律的振幅进行归一化，然后使用EEGLAB中的相差分类工具画出条图.条图中的彩条宽度表示模拟节律的相位稳定性,彩条的宽度与图示值越大，意味着相位稳定性越好，反之亦然.

在上述3种方法中，表示相位稳定性的数值为0～1，1代表模拟节律的相位稳定性不受外界因素的影响，0代表其稳定性受外界影响较大.

2 结果

2.1 偶极子电流相位活动的影响

在各向同性的媒质中，当偶极子的初相由0变为4t2时，PPI值会从1.0降为0.372(图2(a))，图2中的PS值表示偶极子电流初相的影响，其大小会从1.0降为0.372 4，如图2(b)中的玫瑰图所示.同样地，观察图2(c)和图2(d)中各条图的不同颜色条的宽度和图示，发现相位的中心度也在下降.上述结果表明，模拟节律的相位稳定性与节律源相位的非线性变化高度相关.

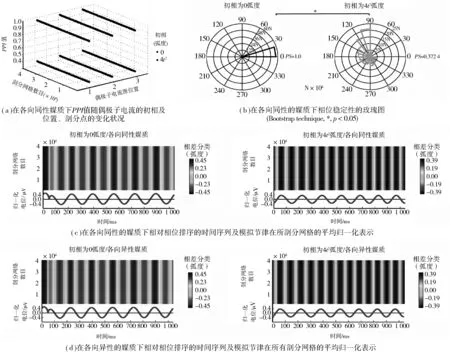
图2 模拟节律的相位稳定性Fig.2 Phase stability of simulated rhythms

2.2 其他因素的影响

从图2(a)中发现，位置1,2,3处的PPI值没有明显的上升或者下降，即其并不会随着偶极子电流源位置的变化而发生改变.同时，当偶极子电流源位于模型中的某一位置时，模型上不同网格上的PPI值也没有出现波动，图2(b)中表现为大部分网格上的相位也会收敛于一条分类线，这些均表明模拟节律的相位与剖分点的位置无关.比较图2(c)和图2(d)可知，当偶极子电流的初相同相位时，即同为0或同为4t2时，不同性质导电媒质上的模拟脑节律的相对相位排序时间序列具有一致性.同时，拥有不同性质的导电媒质上的模拟脑节律在所有网格上具有一致的平均振幅.上述两个结果表明，NBPS与模拟脑模型的导电媒质的导电特性无关.

3 讨论

最近的研究发现，脑节律的平均相位与神经系统的非线性活动相关,而神经系统中的非线性活动受到如生理学、病理学或外界刺激等多种因素的影响[11-12]，本研究借助统计学和窄带相位模型(公式(1)和(2))得到的相关结论受到了上述研究成果的支持.另外，文中与模拟脑节律相位稳定性相关的结果与早期文献的假设一致：非线性会影响脑节律源之间的相互作用，还会引起窄带相位稳定性的变动[13].最后，自我维持系统原理也表明，弱耦合会对节律源的相位一致性产生影响，并且与节律源的振幅无关[14-15].

4 结论

由结果与讨论可知，NBPS只与模拟节律源初相的非线性活动相关，与诸如电导媒质特性、节律源活动等因素无关.

[2] DING N,SIMON J Z.Power and phase properties of oscillatory neural responses in the presence of background activity[J].Journal of Computational Neuroscience,2013,34(2):337-343.

[3] GE M,WANG D,DONG G,et al.Transient impact of spike on theta rhythm in temporal lobe epilepsy[J].Experimental Neurology,2013,250(4):136-142.

[4] ZHENG C,QUAN M,ZHANG T.Decreased thalamo-cortical connectivity by alteration of neural information flow in theta oscillation in depression-model rats[J].Journal of Computational Neuroscience,2012,33(3):547-558.

[5] ZHENG C,QUAN M,YANG Z,et al.Directionality index of neural information flow as a measure of synaptic plasticity in chronic unpredictable stress rats[J].Neuroscience Letters,2011,490(1):52-56.

[6] LOBIER M,SIEBENHÜHNER F,PALVA S,et al.Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions[J].Neuroimage,2014,85(2):853-872.

[7] HAUEISEN J,TUCH D S,RAMON C,et al.The influence of brain tissue anisotropy on human EEG and MEG[J].Neuroimage,2002,15(1):159-166.

[8] WOLTERS C H,ANWANDER A,TRICOCHE X,et al.Influence of tissue conductivity anisotropy on EEG/MEG field and return current computation in a realistic head model: a simulation and visualization study using high-resolution finite element modeling[J].Neuroimage,2006,30(3):813-826.

[9] DELORME A,MAKEIG S.EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis[J].Journal of Neuroscience Methods,2004,134(1):9-21.

[10]SUN J,LI Z,TONG S.Inferring functional neural connectivity with phase synchronization analysis: a review of methodology[J].Computational & Mathematical Methods in Medicine,2012(2):311-321.

[11]LACHAUX J,RODRIGUEZ E,MARTINERIE J,et al.Measuring phase synchrony in brain signals[J].Human Brain Mapping,1999,8(4):194-208.

[12]MORMANN F,LEHNERTZ K,DAVID P,et al.Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients[J].Physica D Nonlinear Phenomena,2000,144(3/4):358-369.

[13]WIENER N.Brain waves and interferometer[J].Journal of the Physical Society of Japan,1956(18):499.

[14]ROSENBLUM M G,PIKOVSKY A S,KURTHS J.Phase synchronization of chaotic rotators[J].Physical Review Letters,2002,88(5):054102.

[15]ROSENBLUM M G,PIKOVSKY A S.Detecting direction of coupling in interacting oscillators[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2001,64(2):322-333.

2016-06-29

河北省高等学校科学技术研究项目(ZD2014026)；河北省高校创新团队领军人才培育项目(LJRC003)

张吉昌(1991-)，男，河南林州人，硕士研究生，研究方向为电力系统及其自动化、生物医学工程.

Q64

A

1674-330X(2016)04-0041-04