APPROXIMATION TO THE FRACTIONAL BROWNIAN SHEET FROM STOCHASTIC INTEGRALS OF POWER FUNCTION

SANG Li-heng,SHEN Guang-jun,XIA Liang-wen

(1.School of Mathematics,Chuzhou University,Chuzhou 239000,China )

(2.Department of Mathematics,Anhui Normal University,Wuhu 241000,China )

APPROXIMATION TO THE FRACTIONAL BROWNIAN SHEET FROM STOCHASTIC INTEGRALS OF POWER FUNCTION

SANG Li-heng1,2,SHEN Guang-jun2,XIA Liang-wen2

(1.School of Mathematics,Chuzhou University,Chuzhou 239000,China )

(2.Department of Mathematics,Anhui Normal University,Wuhu 241000,China )

In this paper,we study an approximation of the fractional Brownian sheet.By using the Wiener integrals,we obtain the approximation by stochastic integrals of power function.

fractional Brownian sheet;stochastic integral;power function

1 Introduction

The self-similarity has become an important aspect of stochastic models in various scientific areas including hydrology,telecommunication,turbulence,image processing and finance.The best known and most widely used process that exhibits the self-similarity property is the fractional Brownian motion(fBm in short).The fBm with Hurst index H∈(0,1)is a zero mean Gaussian process{BH(t),t≥0}with BH(0)=0 and covariance

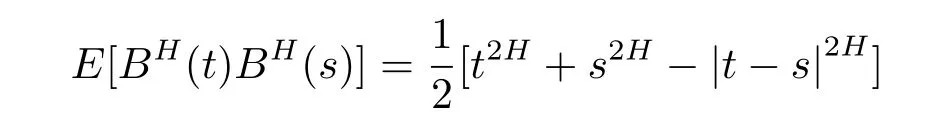
for all s,t≥0.Some surveys about the fBm could be found in Biagini et al.[4],Chen and Xiao[5],Mishura[10],Nualart[11],Wang and Wang[15],Yan[16]and the references therein.

where the kernel KHis given by

with the normalizing constant cH＞0 given by

Many authors studied the approximation of the fBm.For example,Delgado and Jolis[7] proved that BHcan be approximated in law by means of some processes constructed from the standard Poisson process.In Li and Dai[8],a special approximation to the one-parameter fractional Brownian motion is constructed using a two-parameter Poisson process.Mishura and Banna[12]found an approximation of fractional Brownian motion by wiener integrals.

On the other hand,many authors proposed to use more general self-similar Gaussian processes and random fields as stochastic models.Such applications raised many interesting theoretical questions about self-similar Gaussian processes and fields in general.Therefore, some generalizations of the fBm were introduced such as fractional Brownian sheet.

Recall that the fractional Brownian sheet can also be defined by a Wiener integral with respect to the Brownian sheet{B(t,s),(t,s)∈[0,T]×[0,S]}(see,for example,Bardina et al.[1])

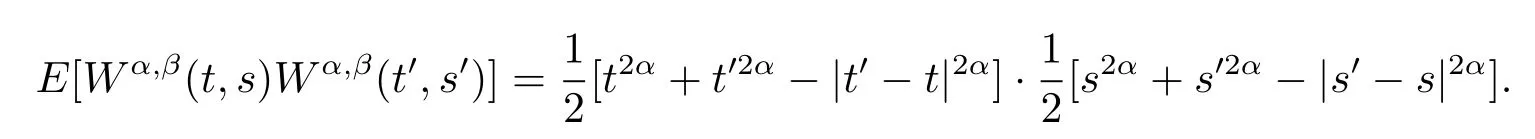
It was proved in Bardina et al.[1]that the fractional Brownian sheet can be weakly approximated by discrete processes constructed from the Poisson process in the space of continuous functions.Tudor[9]generalized this approximation in the Besov space.Wang et al.[13,14] showed that the fractional Brownian sheet can be approximated in distribution by the random walks and martingale differences sequence in the Skorohord space,respectively.We refer to Bardina and Florit[3],Bardina and Jolis[2],and the references therein for more information about weak approximation for the fractional Brownian sheet and multidimensional parameter process.

Motivated by all above results,in this paper,we will consider the approximation of the fractional Brownian sheet with α,β∈from wiener integrals.

More precisely,we consider the following problem.Let T＞0,S＞0 be two fixed number and consider the plane[0,T]×[0,S].Now,let the mapping a:[0,T]×[0,S]→R be a nonrandom measurable function of the square integral space L2([0,T]×[0,S]),that is,a(t,s) is a function such that the stochastic integrala(u,v)B(du,dv),(t,s)∈[0,T]×[0,S]is well defined with respect to the Brownian sheet{B(t,s),(t,s)∈[0,T]×[0,S]}.The problem is to find

The paper is organized as follows.In Section 2,we obtain an approximation of a fractional Brownian sheet by power function with a positive index.In Section 3,we construct an approximation of a fractional Brownian sheet by power function with a negative index, i.e.,a(t,s)=,where k＞0,α,β∈and find the point where the function attains its the minimum value.

2 An Approximation of A Fractional Brownian Sheet by Power Function with A Positive Index

Let Wα,β={Wα,β(t,s),(t,s)∈}be a fractional Brownian sheet with Hurst index α,β∈the number T,S＞0 be fixed,a(t,s)∈L2([0,T]×[0,S])is a measurable function.M(t,s),(t,s)∈[0,T]×[0,S]is a square integrable martingale which have the form

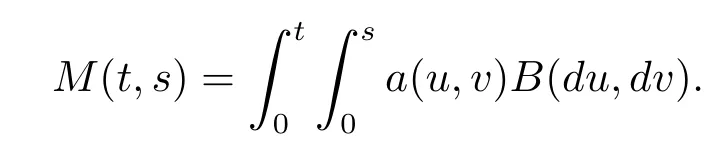
In this section,we will evaluate

where A⊂L2([0,T]×[0,S])is some class of functions.

Lemma 2.1If the Lebasgue measure of the set A={(t,s)∈[0,T]×[0,S]:a(t,s)＜0} is positive,then we cannot attained the minimum in(2.1)at a function a∈A.

Proof

This makes it clear that if one changes a(u,v)for-a(u,v),at the points(u,v)where a(u,v)＜0,then the right hand side of(2.2)does not increase.This completes the proof.

Theorem 2.2Among all function a∈L2([0,T]×[0,S])such thatnondecreasing with respect to t and s,then the minimum in(2.1)is attained at the function,where cα,cβis given by cα=

ProofLet φ(t,s)be the right hand of the equation(2.2),that is,

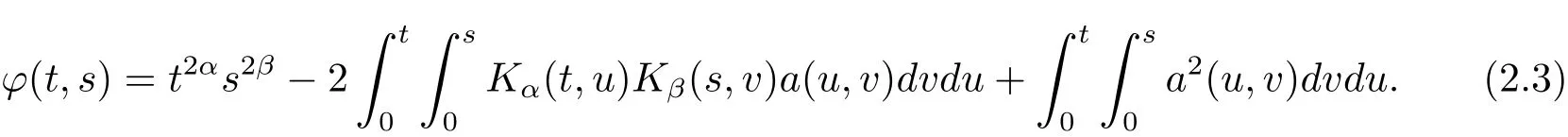
Partial differentiating the right hand of(2.3)with respect to t,we get

Next,partial differentiating the right hand of(2.4)with respect to s,we get

Changing the variable u=tx,v=sy in the integral,we obtain

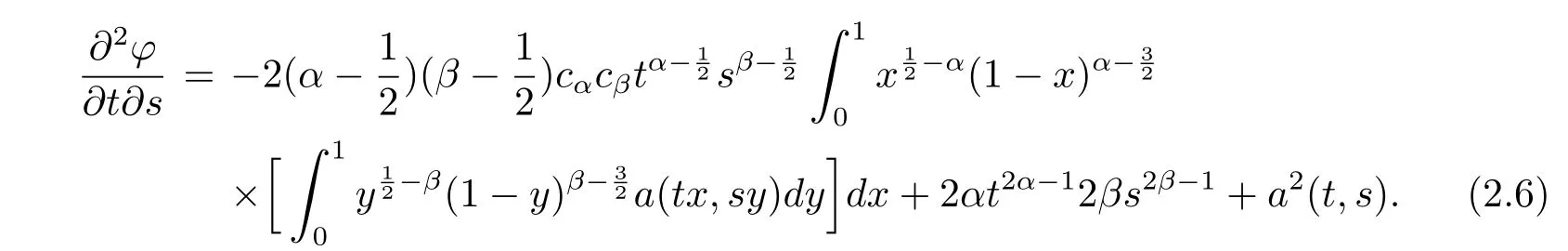
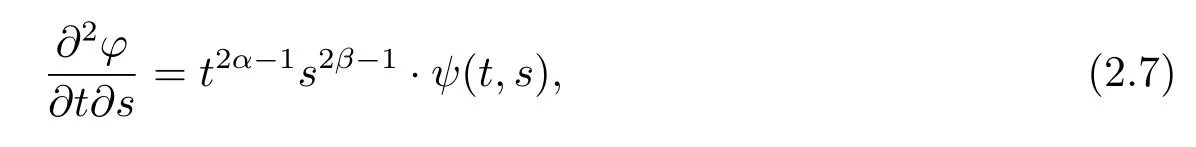
where

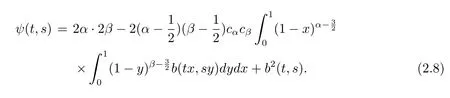
Similarly,if we differentiate(2.3)with respect to s and then t,the equation(2.5)can also be attained,because the variable s and the variable t are symmetry in(2.5).So we don’t need to consider the precedence of the partial differential about t and s.

If the function b(t,s)is nondecreasing with respect to t and s,i.e.,b(tx,sy)≤b(t,sy)≤b(t,s),where x,y∈(0,1).Thus

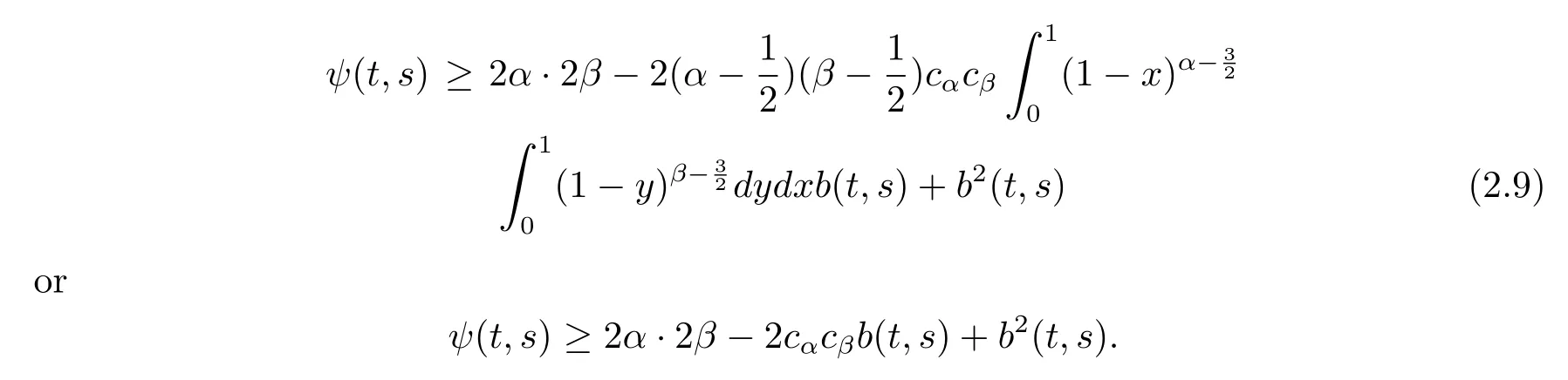
Next,we consider the discriminant of the quadratic polynomial x2-2cαcβx+2α·2β, so the discriminant is represented as follows:

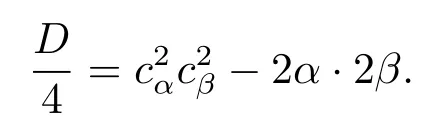
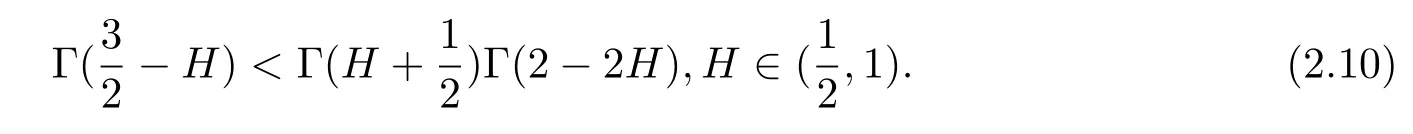
Thus the discriminant D is negative,whence ψ(t,s)≥0,and the minimal value of ψ(t,s)is attained at b(t,s)=cαcβ.

Now,we show that the b(t,s)=cαcβcan also make φ(t,s)a minimal value.Further, we obtain

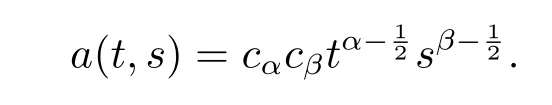
Following the assumption of the b(t,s),we have the form of the function a(t,s)=Because b(t,s)=cαcβis a constant,so we let a(t,s)=,and substituting it to(2.3).

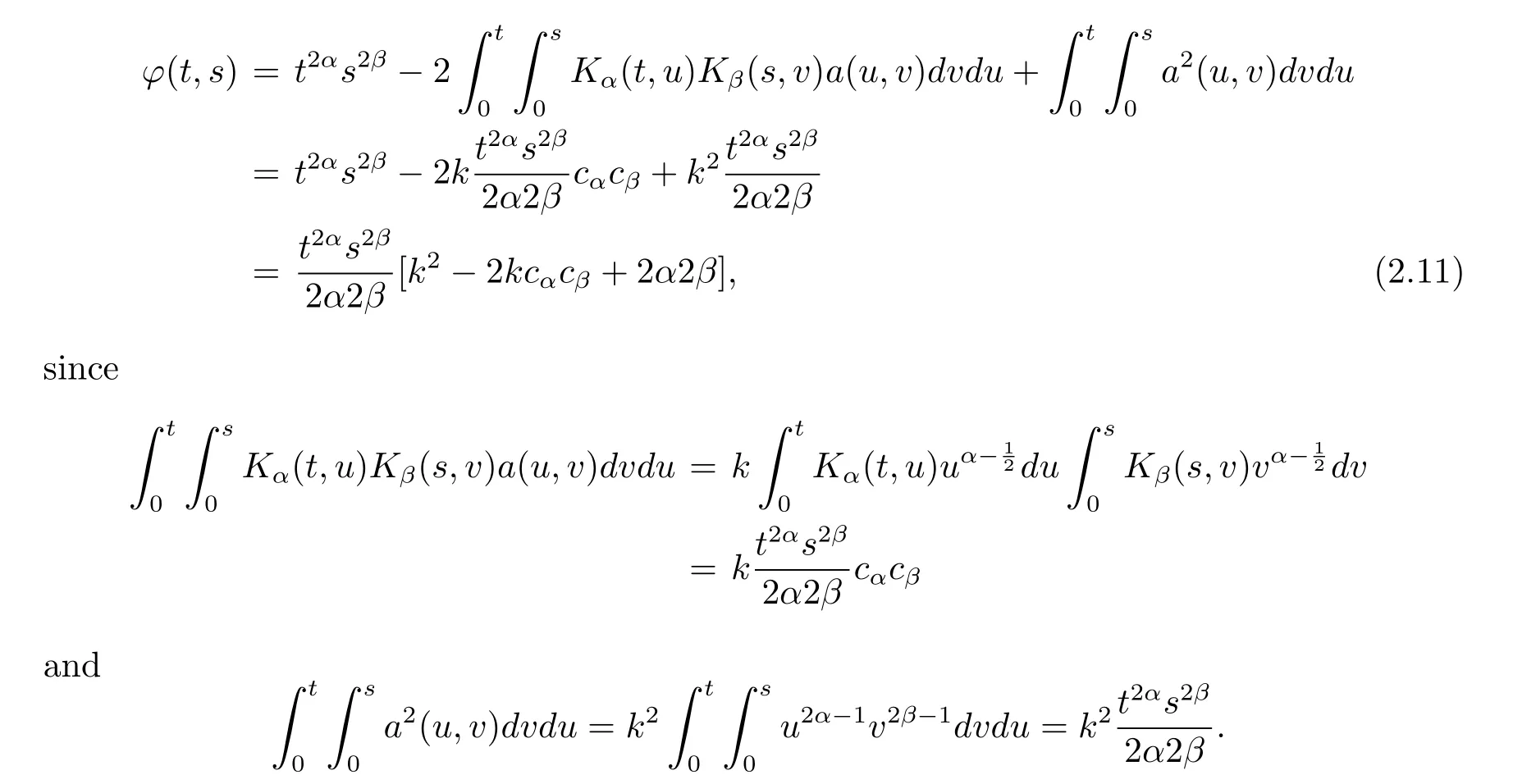
Hence,when k=cαcβ,φ(t,s)have a minimal value 2α·2β-Thus the minimum among all a(t,s)such that b(t,s)=is nondecreasing is attained at b(t,s)=cαcβ.

3 An Approximation of a Fractional Brownian Sheet by Power Function with A Negative Index

From Lemma 2.1,we obtain that the square integral function a(t,s)is positive,and we get an approximation of a fractional Brownian sheet by power function with a positive index in Theorem 2.2.In this section,we try to construct an approximation of a fractional

Brownian sheet by power function with a negative index,that is,a(t,s)=,where k＞0,α,β∈In fact,if k≤0,then a(t,s)≤0,while the kernel of a fractional Brownian sheet is positive number.So,it is unreasonable to use a(t,s)≤0 to approximate the kernel of a fractional Brownian sheet.

Let

then we need to evaluate

Lemma 3.1(1)The function f(t,s,k)admits the following representation:

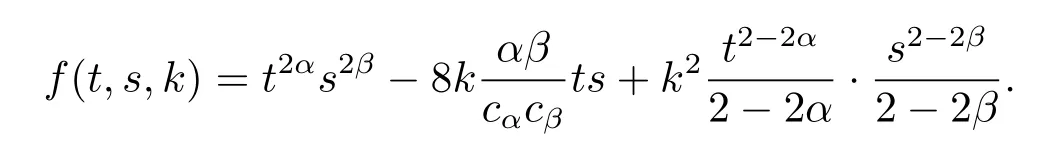
(2)For all k∈R+,

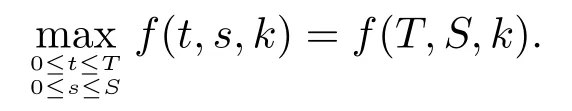
ProofBy the straightforward calculations,we have

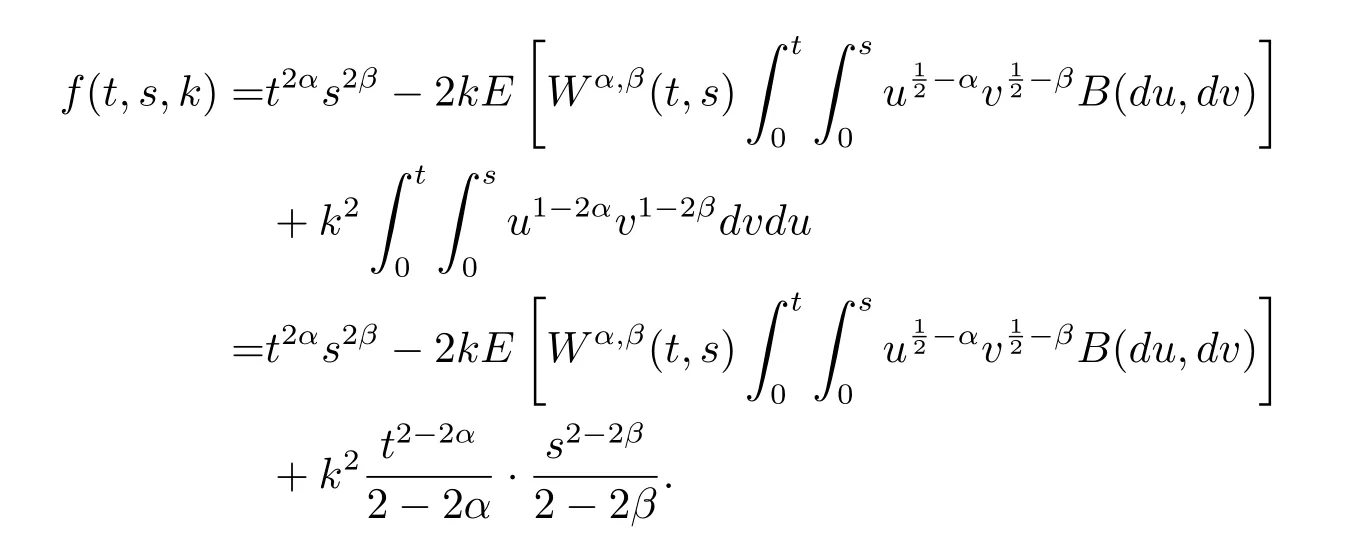
According to representation(1.1),we have

since

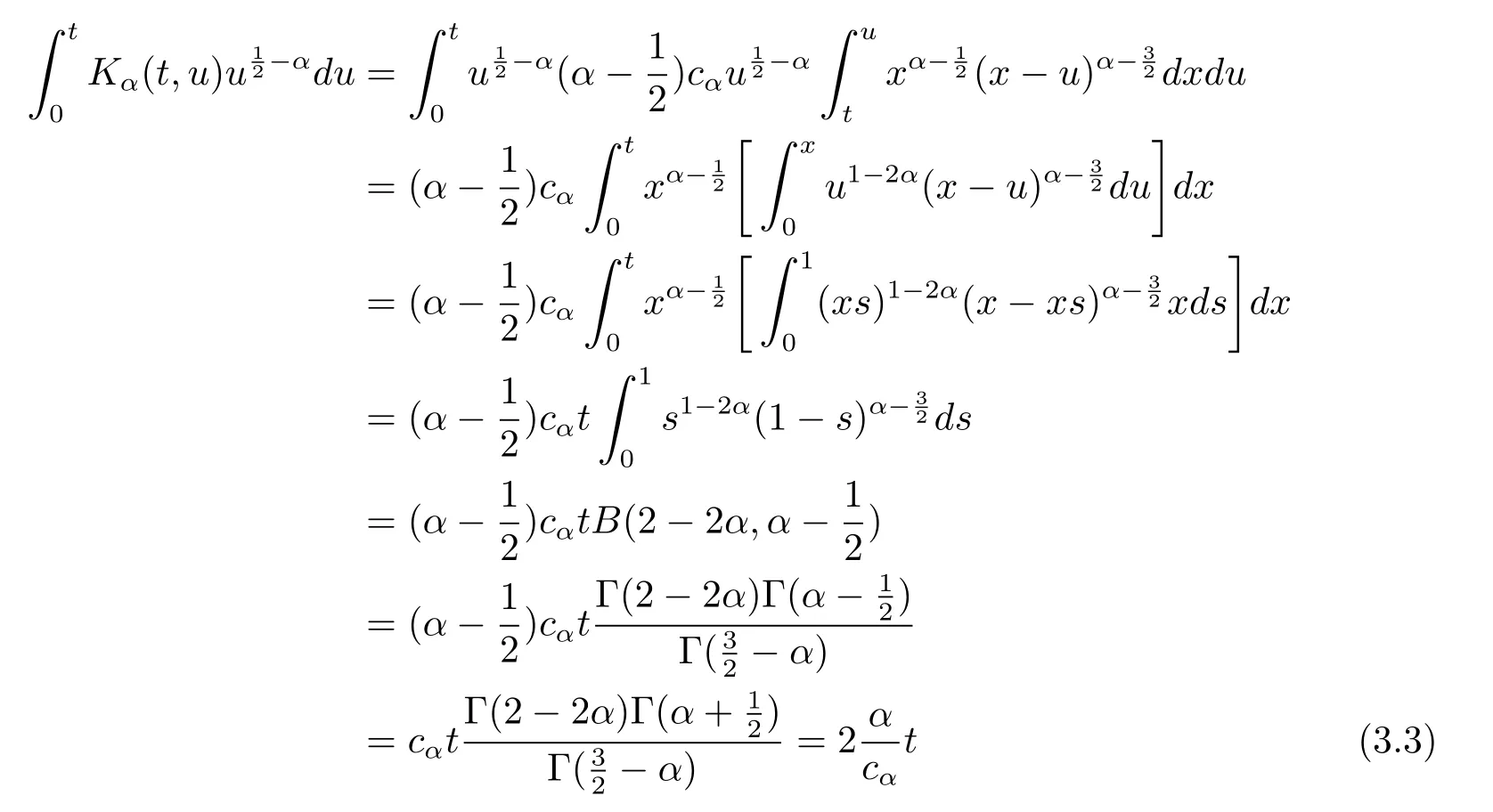
and

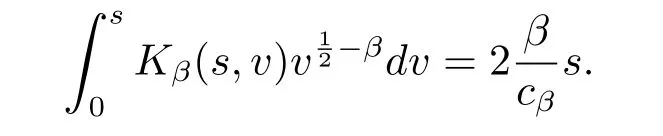
This completes the proof of assertion(1).

Assertion(2).Differentiating the function f with respect to t,we have

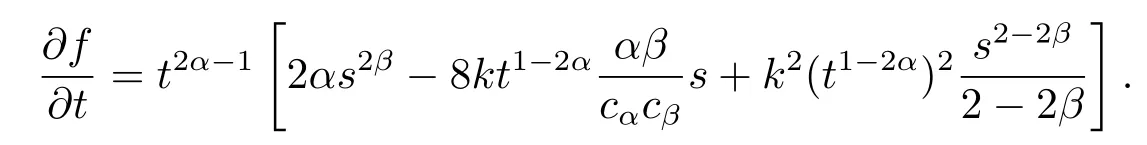
Let x=kt1-2α,we consider the discriminant

of the follow equation

since(2β)2(2-2β)＜＜2β,and the distance between(2β)2(2-2β)andis longer than the distance ofand 2β.Hence＜0.So the roots of equation(3.5)is not exist with respect t in R+.We obtain thatis positive.Hence,f(t,s,k)is nondecreasing for all t.Similarly,we also obtain that f(t,s,k)is nondecreasing for all s.Following the above discussion,we get

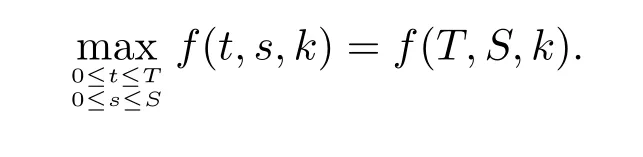
Now,from Lemma 3.1,we easily obtain the following main result.

Theorem 3.2Let A={a(t,s)=

ProofFirst of all,we calculate the value of the constant k which makesa minimal value.

Following assertion(2)of Lemma 3.1,we have

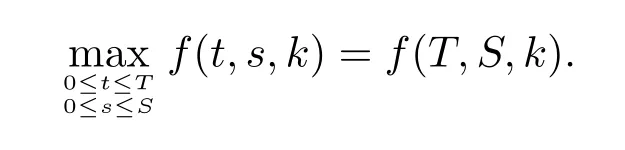
So we need evaluate the k such that the minimum of f(T,S,k)can be attained at the k in the next work,that is,

Now,differentiating f(T,S,k)with respect to k,

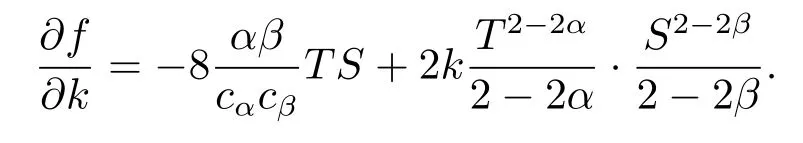
Then we have

This completes the proof.

[1]Bardina X,Jolis M,Tudor C A.Weak convergence to the fractional Brownian sheet and other two-parameter Gaussian processes[J].Statist.Probab.Lett.,2003,65:317–329.

[2]Bardina X,Jolis M.Weak convergence to the fractional Brownian sheet from the Poisson process in the plane[J].Bernoulli.,2000,6(4):653–665.

[3]Bardina X,Florit C.Approximation in law to the d-parameter fractional Brownian sheet based on the functional invariance principle[J].Rev.Mat.Iberoam.,2005,21(3):1037–1052.

[4]Biagini F,Hu Y,Øksendal B,Zhang T.Stochastic calculus for fBm and applications[M].New York: Springer-Verlag,2008.

[5]Chen Z,Xiao Y.On intersections of independent anisotropic Gaussian random fields[J].Sci.China Math.,2012,55(11):2217–2232.

[7]Delgado R,Jolis M.Weak approximation for a class of Gaussian processes[J].J.Appl.Probab., 2000,37(2):400–407.

[8]Li Y,Dai H.Approximations of fractional Brownian motion[J].Bernoulli.,2011,17(4):1195–1216.

[9]Tudor C.Weak convergence to the fractional Brownian sheet in Besov spaces[J].Bull.Braz.Math. Soc.,2003,34(3):389–400.

[10]Mishura Y.Stochastic calculus for fBms and related processes[M].New York:Springer,2008.

[11]Nualart D.Malliavin Calculus and related topics(2nd edition)[M].New York:Springer,2006.

[12]Mishura Y S,Banna O L.Approximation of fractional Brownian motion by wiener integrals[J]. Theor.Prob.Math.Stat.,2009,79:107–116.

[13]Wang Z,Yan L,Yu X.Weak approximation of the fractional Brownian sheet from random walks[J]. Electron.Commun.Prob.,2013,18(90):1–13.

[14]Wang Z,Yan L,Yu X.Weak approximation of the fractional Brownian sheet using martingale differences[J].Stat.Prob.Lett.,2014,92:72–78.

[15]Wang B B,Wang Z H.Rate of convergence for fractional stratonovich integral[J].J.Math.,2010, 30(6):983–986.

[16]Yan L.The fractional derivatives for local time of fBm with Hurst index large than 1/2[J].Math. Zeitschrift,to appear,2015.

分数布朗单的幂函数随机积分逼近

桑利恒1,2,申广君2,夏良文2

(1.滁州学院数学学院,安徽滁州239000)

(2.安徽师范大学数学系,安徽芜湖241000)

本文研究了分数布朗单的逼近问题.利用Wiener积分,得到了分数布朗单的幂函数型随机积分逼近.

分数布朗单;随机积分;幂函数

O211.6

tion:60H05;60G22

A

0255-7797(2017)01-0074-09

∗Received date:2015-01-29Accepted date:2015-03-19

Foundation item:Supported by the National Natural Science Foundation of China(11271020) and the Natural Science Foundation of Universities of Anhui Province(KJ2012Z284;KJ2012Z286).

Biography:Sang Liheng(1983–),male,born at Taihe,Anhui,master,major in stochastic process.

Shen Guangjun.