换热单元协进化的微分进化算法优化换热网络的性能

陈 上，崔国民，张春伟，段欢欢

（上海理工大学 新能源科学与工程研究所，上海 200093）

换热单元协进化的微分进化算法优化换热网络的性能

陈 上，崔国民，张春伟，段欢欢

（上海理工大学 新能源科学与工程研究所，上海 200093）

采用微分进化算法应用于换热网络综合时，针对换热网络分级超结构模型中的整型变量即换热器有无问题，提出两种换热器协进化策略，分别利用差分进化原理与最小换热潜能约束实现换热单元协进化生成与消去，结合微分进化算法搜索合理的换热单元匹配。通过两个经典算例分析证明了算法的有效性，寻找到了更加符合实际生产的换热网络结构，优化结果较文献的年综合投资费用更低，用于工业生产过程中，可以稳定有效地节约成本。

换热网络综合；换热器协进化；微分进化算法

换热网络是化工过程中一个关键的子系统，其优化方法主要分为热力学方法和数学规划方法。以窄点技术法［1］为代表的热力学优化方法广泛应用于过程系统的综合及优化，虽然窄点法是一种分步优化方法，但其具有极强的可操作性，在热力学理论指导下的优化方法更容易得到适合于工业应用的设计结果。Yee等［2］将投资费用和运行费用结合在一起同时优化，并提出级的概念建立换热网络Grossmann分级超结构模型，使得数学规划法也被应用于换热网络优化问题上。数学规划法的优点是可以由计算机完成匹配及自动搜索，换热网络综合优化中通常采用确定性方法来处理连续变量。Athier等［3］采用局部优化程序库中NLP算法、Lewin等［4］采用Simplex算法、Errico等［5］采用Lindo-Lingo和CPLEX程序来优化连续变量。但整个模型具有严重的非线性和多峰性，极容易陷入局部极值，因此采用梯度搜索方向的确定性方法很难获得全局最优解。而启发式算法可以处理传统优化算法较难解决的问题，不会因为问题的非凸非线性而过早地陷入局部最优解，因此启发式算法正在成为换热网络全局最优化的一种主流方法。遗传算法［6］、模拟退火算法［7］，粒子群算法［8-9］等已在换热网络综合问题上得到广泛应用。

但换热网络的结构优化即代表换热器有无的0-1整型变量优化仍没有合适的解决方法。尤其是针对较大规模换热网络问题，在利用分级超结构模型计算时，为了保证足够大的求解域，模型的级数至少需要设置在3级以上，这就造成了变量维数即网络中待优化的换热单元数的急剧增大，因此整型变量的优化处理是一个不可忽视的问题。

本工作利用微分进化（DE）算法的差分变异能力与流股最小换热潜能约束，提出两种换热器协进化策略，对换热网络问题中的换热器有无的整型变量进行优化处理，达到换热器协进化生成与消去的目的，进一步改进了DE算法优化换热网络的效能与实用性。并结合算例分析，获得了较以往文献更优的换热网络结构设计。

1 换热网络数学模型

1.1 换热网络问题描述

假设有冷流体（NC）需要加热，热流体（NH）需要冷却，利用冷、热物流的匹配，回收过程中流体的能量。已知冷、热物流的进口温度、目标温度、热容流率及各换热器换热系数；同时，为未达到目标温度的流体设置热、冷公用工程，公用工程的进、出口温度已知。根据冷、热流体的匹配顺序形成一个换热网络，在所有网络流体达到目标温度的情况下，最小化换热网络的设备费用与运行费用。设备费用包括换热器固定投资费用与换热器面积费用，运行费用为公用工程的消耗量。本工作的换热网络结构的表达方式为Grossmann无分流分级结构模型，其中，换热网络级数为NK，最大换热器个数为NKNCNH。以2股热流体与3股冷流体为例，图1为换热网络无分流的分级超结构模型。

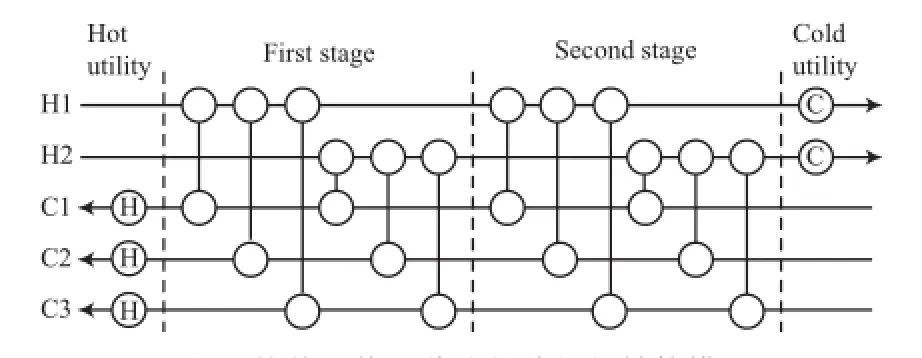
图1 换热网络无分流的分级超结构模型Fig.1 Super-structure of heat exchanger networks(HEN) without stream split.H1，H2：hot fuids；C1，C2，C3：cold fuids.

1.2 换热网络目标函数

换热网络优化问题的目标函数为年综合费用（F），其数学表达式见式（1）。

式中，FEX为固定投资费用，$/a；FA为所有换热单元的面积费用，$/a；FHU，FCU分别为热、冷公用工程的年运行费用（HU代表热公用工程，CU代表冷公用工程），$/a；C2为换热器面积费用系数；A为换热器面积，m2；k代表超结构第k级；i，j分别代表第i股热流体与第j股冷流体；C0为换热器固定投资费用系数；C1为公用工程费用系数；Z为换热器是否存在整型变量，存在时取1，不存在时取0。具体热力学平衡关系及约束条件的描述见文献［10］。

取每个换热器的换热量（Q）为优化变量，依据模型中的假设，冷热流股逆流布置。传热计算中，单个换热器满足热平衡关系式（2）～（3）。

式中，与分别为流股经过换热器的进口与出口温度，℃；Uij为换热器换热系数；GCpij为流股热容流率；LMTDkij为对数平均温差。

由（4）～（5）式计算：

当GCpi=GCpj时，可采用算术平均温差（AMTDkij）代替，即得到式（5）：

当Q大于0时，表示此处存在换热器即Z取1，Q等于0时，则表示此处不存在换热器即Z取0，当Q小于0时则加约束惩罚。此外，在整个数学模型中，还包括如下约束关系式（6）～（13）。1）单股流体热平衡：

2）冷热流股可行出口温度：

3）冷热公用工程热平衡：

式中，TIN和TOUT分别为工程要求的流股进口温度和目标温度，℃；Qkij为冷热流股匹配换热器的换热量，kW；QCU与QHU分别为冷热公用工程量，kW；和分别为冷热流股最末端出口温度，℃。以上约束均采用外点罚函数法进行约束。

2 换热单元协进化的DE算法

2.1 基本DE算法优化换热网络

DE算法是启发式方法的一种，在求优过程中具有高效性、收敛性、鲁棒性等优点［10-12］。同所有的进化算法一样，DE算法也是对候选解的种群进行操作，利用实数值参数向量作为每一代的种群，利用随机偏差扰动产生个体，具有非常好的收敛性与自适应能力。DE算法优化换热网络主要有以下4个步骤。

2.1.1 初始化种群

在求解域随机生成初始种群，设置种群规模，本工作中所优化算例的种群规模都为N=10D，D为最大换热器个数，比例因子CF∈［0，1］，交叉概率CR∈［0，1］。随机生成N组初始点，表示为Q={Q1G，Q2G，…，QN-1G，QNG}，其中，QiG={QiG（1），QiG（2），…，QiG（n）}，QiG为G代种群中第i个个体，相应的各个换热单元的换热量QiG（n）在可行域内生成。

2.1.2 变异

对应第G代进化，变异机制见式（14）。

式中，ViG为变异个体；QBestG为当前种群中的最佳个体；QiG当前目标个体；Qr1G与Qr2G为种群中随机抽取的4个个体；比例因子CF=0.5。

2.1.3 交叉

令交叉概率CR=0.1，对应第G代进化，按式（15）方式生成测试个体。

式中，为第j个目标个体的第i个试探换热量；r为［0，1］均匀分布的随机数；JR为［1，N］范围内随机抽取的整数。

2.1.4 选择

基于DE算法的贪婪进化原则，只选择测试个体和当前个体中的费用较小者进入下一代搜索，见式（16）。

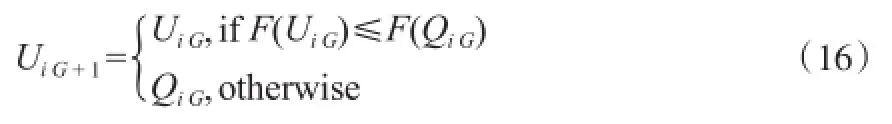
终止条件为当前进化代数达到最大迭代步数，则迭代结束，算法终止，否则G=G+1转到步骤2.1.2节。

2.2 换热单元协进化的DE算法

2.2.1 换热单元协进化生成策略

在换热单元协进化变异过程中，个体在变异时不进行换热器有无的判断，如果个体的当前换热器不存在（即换热量为0），但其对应的变异后换热器换热量大于0，那么进行变异操作后该换热器则生成。例如针对一个两股热流体与两股冷流体的两级换热网络分级超结构模型，每个个体存在8个换热器，选取任意2个个体做差分变异（见式（17））：

其中，qi，q′i和q″i分别为QBestG，Qr1G和Qr2G第i号换热器的换热量，i=1，2，…，8。

r1个体中，第2，7号换热器无换热量；r2个体中，第4，6，7号换热器无换热量，则2个个体在变异过程中，根据公式（14），第2，4，6号换热器会根据交叉概率以一定几率生成换热器，以2号换热器为例：

变异后2号换热器生成，如果该变异使当前个体所对应的换热网络F下降，则该换热器的生成是有效的，并在进化过程中使2号换热器生成，否则此换热器不生成，最终达到优化过程中换热器协进化生成的目的。此外，由于该换热器的生成是遵循差分进化公式，充分利用了算法的进化能力，符合进化规律，有利于算法后期寻找更优的结构以达到更好的全局搜索效果。

2.2.2 换热单元协进化消去策略

在利用DE算法优化换热网络时，针对分级超结构模型，同样以2股热流体与2股冷流体的2级换热网络分级超结构模型为例，每个结构可存在8个换热器（即8个待优化变量），但从换热网络实际工业生产的角度来分析，合理的网络结构只包含2～4个换热器，明显少于8个换热器，因此换热器的合理消去是整形变量优化的关键，尤其是在考虑换热器固定投资费用时，换热单元数是一个不可忽视的优化变量，基于此，本工作提出了换热单元协进化消去策略。

在算法的变异过程中有式（20）和式（21）的判断，若满足则使当前换热器换热量为0即消去该换热器。此后根据DE算法的交叉与选择操作来决定是否在进化过程中消去该换热器并产生新的个体，同样如果该个体所对应的换热网络F下降，则该换热器的消去是有效的，以达到换热单元协进化消去的目的。

式中，Qmin为最小换热潜能约束，算例中Qmin设定为换热潜能最小流体所对应的换热潜能；Q（i）表示当前个体所对应的换热器，然后取随机数R∈［0，1］。

从热力学角度来讲，换热潜能较小的流体其所需的换热单元数相对较少，而在分级超结构中每股流体的可分配换热器数是相同的，那么在进化过程中必然导致换热器分配不均的情况，因此以最小换热潜能为基准对每个换热器进行概率筛选，在保留换热效能较大的换热器情况下，消去换热效能较小的换热器，同时也能在一定程度上减少换热潜能小的流体上多余的换热器。此外，由于该消去过程是基于DE算法的交叉选择操作来决策的，并且以结构的F下降为前提，所以整个过程是一个协进化消去过程。结合基本DE算法可以得到算法程序流程图见图2。

图2 算法程序流程Fig.2 Flow chart of the algorithm.

3 算例分析

3.1 算例1

采用文献［13-15］报道的算例（算例1），过程流体由4股热流体和5股冷流体组成。图3为算例1换热网络结构图。

图3 算例1换热网络结构图Fig.3 HENs of case 1.

表1为算例1流股参数。算例的所有初始参数和费用参数同文献［13-15］。

表1 算例1流股参数Table 1 Stream data for case 1

H1-H4：hot fluids；C1-C5：cold fluids；TIN：inlet temperature；TOUT：target temperature；MCp： heat capacity flow rate；h：heat transfer coefcient；HU：hot utility；CU：cold utility.

利用换热器协进化生成与消去策略结合DE算法优化算例时，记录最优个体换热器台数变化曲线（不包括公用工程），见图4。从图4可看出，从初始生成的12个换热器经过协进化生成消去过程后，换热器台数最少消去到8个换热器，最后在算法后期稳定在9个换热器。

图4 算例1最优个体换热器台数变化曲线Fig.4 Curve of the best number of individual heat exchangers for case 1.

算例1与文献值的对比结果见表2。由表2可知，该网络设计更符合实际工业生产需要，成本较高的热公用工程需求量明显少于文献［11-13］报道的结果（降低了18 046 $/a），表明更多的内部热量被回收利用，缺少的冷量则被成本较低的冷公用工程补偿。3.2 算例2

表2 算例1与文献值的对比结果Table 2 Comparison between the results of case 1 and literature data

采用文献［15-18］报道的算例（算例2），过程流体由6股热流体与4股冷流体组成，图5为算例2换热网络结构图。

冷、热流体及公用工程的初始温度和目标温度、热容流率见表3。

图5 算例2换热网络结构图Fig.5 HENs of case 2.

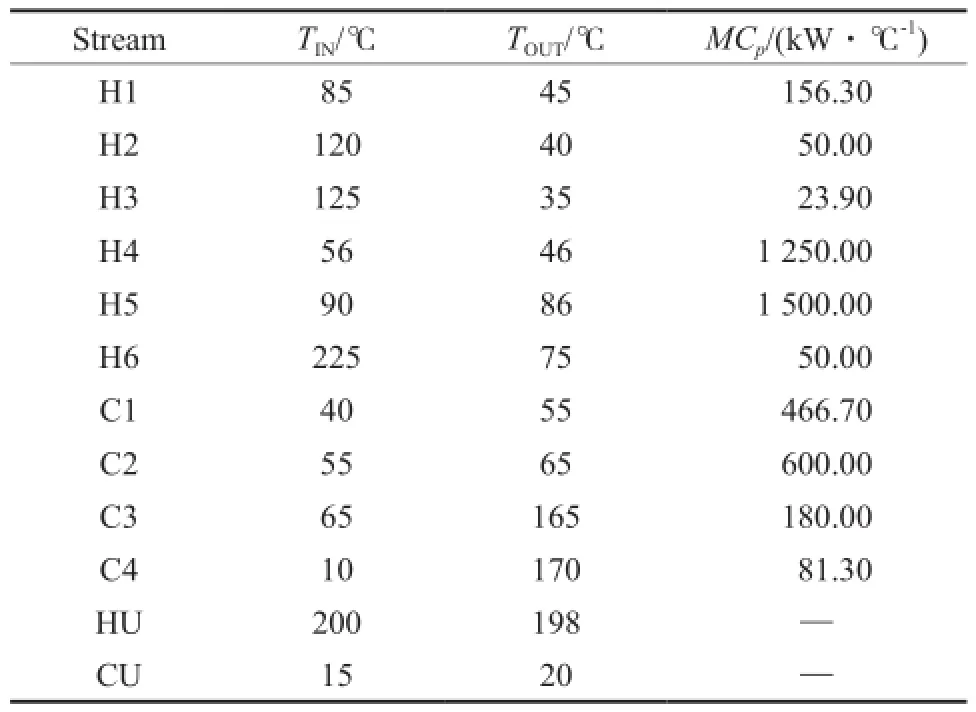
表3 算例2流股参数Table 3 Stream data for case 2

图6为算例2最优个体换热器台数变化曲线。由图6可知，从初始生成的15个换热器经过协进化生成和消去过程后，换热器台数最多增加到20个换热器，最后在算法后期稳定在19个换热器。

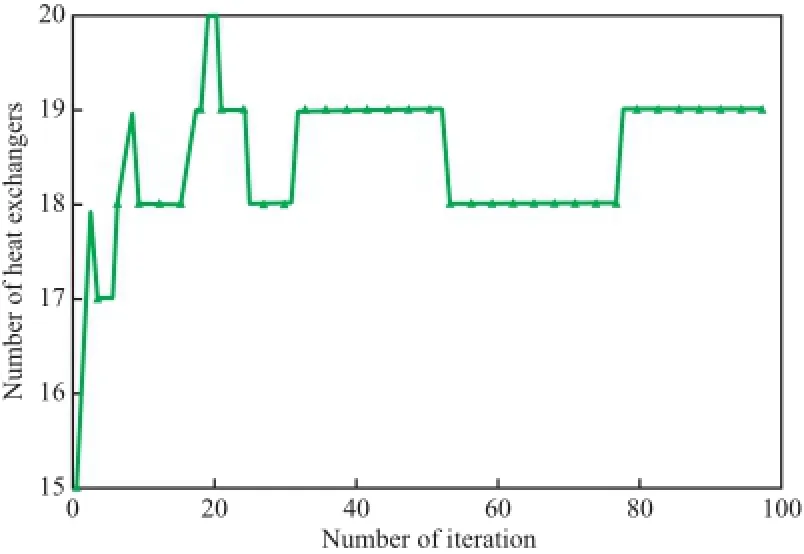
图6 算例2最优个体换热器台数变化曲线Fig.6 Curve of the best number of the individual heat exchangers for case 2.

表4为算例2与文献值的对比结果。由表4可得出较以往文献年综合费用更低的换热网络设计，较文献值［13］降低了16 290 $/a。

表4 算例2与文献值的对比结果Table 4 Comparison between the results of case 2 and literature data

结合以上2个算例可发现，本工作提出的换热单元协进化策略结合DE算法能很好地应用在换热网络优化中，其中，算例1由12个换热器最终减少到9个，算例2由15个换热器最终增加到19个，分别证明了换热单元协进化消去与生成的最终效果，体现出了改进算法的稳定性。同时，这种考虑最小换热潜能约束的协进化策略，使得算法优化得出的换热器台数较单纯算法优化后的更加合理，尤其在算例1中，文献［15］报道的结果有18台换热器（包括公用工程），而本工作的优化结果只有14台换热器，而在算例2中虽然换热单元数没有太大的变化，但换热单元的面积总和明显小于文献值［15］，节省了换热单元的面积总和约536 m2，2个优化结果都具有更好的工程实际用途，进一步证明了算法的实用性，在工业生产中，可以稳定有效地节约成本。

4 结论

1） 将换热网络分级超结构模型中的整型变量即换热器有无问题，转化为换热单元换热量大小的问题即连续变量优化问题，简化了模型的计算复杂性。

2） 提出换热单元协进化的微分进化算法优化换热网络整体性能，利用算法的进化能力控制换热器的台数，通过差分进化的原理使换热单元协进化生成。

3） 利用最小换热潜能约束实现换热单元协进化消去，最终寻找到合理的换热网络结构。

4） 通过算例证明了算法的有效性，优化结果较文献有很大的改进，降低年综合费用，节约生产成本，并且更符合实际工业生产的需要。

符 号 说 明

［1］Linnhoff B，Hindmarsh E. The pinch design method for heat exchanger networks［J］. Chem Eng Sci，1983，38（5）：745 -763.

［2］Yee T F，Grossmann I E. Simultaneous optimization models for heat integration：Ⅱ. Heat exchanger network synthesis［J］. Comput Chem Eng，1990，14（10）：1165 - 1184.

［3］Athier G，Floquet P，Pibouleau L，et al. Optimization of heat exchanger networks by coupled simulated annealing and NLP procedures［J］. Comput Chem Eng，1996，20（12）：13 - 18.

［4］Lewin D R，Wang Hao，Shalev O. A generalized method for HEN synthesis using stochastic optimization：I. General framework and MER optimal synthesis［J］. Comput Chem Eng，1998，22（10）：1503 - 1513.

［5］Errico M，Maccioni S，Tola G，et al. A deterministic algorithm for the synthesis of maximum energy recovery heat exchanger network［J］. Comput Chem Eng，2007，31（7）：773 - 781.

［6］Soltani H，Shafei S. Heat exchanger networks retroft with considering pressure drop by coupling genetic algorithm with LP and ILP methods［J］. Energy，2011，36（5）：2381 - 2391.

［7］Özdamar L. New simualted annealing algorithms for constrained optimization［J］. Asia Pac J Oper Res，2010，27（3）：347 - 367.

［8］Huo Zhaoyi，Zhao Liang，Yin Hongchao，et al. Simultaneous synthesis of structural-constrained heat exchanger networks with and without stream splits［J］. Can J Chem Eng，2013，91（5）：830 - 842.

［9］Huo Zhaoyi，Zhao Liang，Yin Hongchao，et al. A hybrid swarm intelligence algorithm for simultaneous synthesis of heat exchanger network［J］. CIESC J，2012，63（4）：1123 - 1123.

［10］Storn R，Price K. Diferential evolution：A simple and efcient heuristic for global optimization overcontinuous spaces［J］. J Glob Opt，1997，11（4）：341 - 359.

［11］Wang Yong，Li Hanxiong，Huang Tingwen，et al. Diferential evolution based on covariance matrix learning and bimodal distribution parameter setting［J］. Appl Soft Comput，2014，18：232 - 247.

［12］Brest J， Zamuda A， Fister I， et al. Large scale global optimization using self-adaptive diferential evolution algorithm［C］// 2010 IEEE Congress on Evolutionary Computation（CEC）. Curran associates inc：Barcelona，2010：1 - 8.

［13］Zhu X X，Oneill B K，Roach J R，et al. A method for automated heat exchanger network synthesis using block decomposition and non-linear optimization［J］. Chem Eng Res Des，1995，73（A8）：919 - 930.

［14］Briones V，Kokossis A C. Hypertargets：A conceptual programming approach for the optimisation of industrial heat exchanger networks：I. Grassroots design and network complexity［J］. Chem Eng Sci，1999，54（4）：519 - 539.

［15］方大俊，崔国民. 微分进化算法应用于换热网络全局最优化［J］. 化工学报，2013，64（9）：3285 - 3290.

［16］Ravagnani M，Sliva P A，Arroyo A，et al. Constantino，heat exchanger network synthesis and optimisation using genetic algorithm［J］. Appl Therm Eng，2005，25（7）：1003 -1017.

［17］Krishna M，Yerramsetty，Murty C V S. Synthesis of cost-optimal heat exchanger networks using diferential evolution［J］. Comput Chem Eng，2008，32（8）：1861 - 1876.

［18］Khorasany R M，Fesanghary M. A novel approach for synthesis of cost-optimal heat exchanger networks［J］. Comput Chem Eng，2009，33（8）：1363 - 1370.

（编辑 杨天予）

Optimization of heat exchanger network by cooperative differential evolution algorithm of heat exchange unit

Chen Shang，Cui Guomin，Zhang Chunwei，Duan Huanhuan
（Research Institute of New Energy Science and Technology，University of Shanghai for Science and Technology，Shanghai 200093，China）

The diferential evolution algorithm was applied to heat exchanger network synthesis. Aimed at the existing integer variable problems in the super structure model，two strategies for the heat exchanger cooperation evolution were proposed，using the differential evolution principle and the minimal heat load constraint for the generation and elimination of the cooperation evolution of heat exchange units in order to find reasonable heat exchange unit matching by the combination of the diferential evolution algorithm. The efectiveness of the algorithm was demonstrated through two classic examples and the heat exchanger networks in line with actual production were found. The total annual cost after the optimization was lower than those in literatures.

heat exchanger network synthesis；heat exchanger self-adaption；diferential evolution algorithm

1000 - 8144（2016）04 - 0474 - 07

TK 124

A

10.3969/j.issn.1000-8144.2016.04.016

2015 - 10 - 23；［修改稿日期］2015 - 12 - 19。

陈上（1991—），男，湖北省仙桃市人，硕士生，电邮 chenshang926@163.com。联系人：崔国民，电话 021 - 55271466，电邮cgm1226@163.com。

国家自然科学基金资助项目（51176125）；沪江基金研究基地专项（D14001）。