X射线大视场相衬成像位移误差的数值分析

黄建衡，雷耀虎，刘 鑫，郭金川，李 冀，郭宝平

1) 深圳大学光电工程学院，光电子器件与系统教育部/广东省重点实验室,广东深圳 518060; 2)深圳大学信息工程学院，广东深圳 518060

【光电工程 / Optical Engineering】

X射线大视场相衬成像位移误差的数值分析

黄建衡1,2，雷耀虎1，刘 鑫1，郭金川1，李 冀1，郭宝平1

1) 深圳大学光电工程学院，光电子器件与系统教育部/广东省重点实验室,广东深圳 518060; 2)深圳大学信息工程学院，广东深圳 518060

随着X射线光栅相衬成像视场的扩大，相位步进法中的位移误差会对相衬图像造成很大影响．提出一种X射线大视场光栅相衬成像位移误差的数值分析方法，通过数值计算获得不同位移误差下两个聚苯乙烯小球的相衬成像结果．理论模型的数值计算结果表明，位移误差会导致小球相衬图像产生明暗条纹的背景干扰，位移误差越大，其相衬图像受背景条纹的干扰越严重．当位移误差达到光栅周期的1/10时，小球相衬信息几乎被背景条纹所淹没，致使其边缘信息无法识别．要获得背景均匀的大视场相衬图像，则位移误差最好控制在光栅周期的1/100以下．分析结果可为X射线大视场相衬成像系统的设计提供参考依据．

光学工程；X 射线；相衬成像；相位步进法；位移误差；视场

自伦琴发现X射线以来，X射线成像技术已被广泛用于探测物体内部结构．虽然传统X射线吸收成像技术对轻元素物质成像衬度低，但是因为轻元素物质对X射线相位的改变量是对其振幅改变量的103倍[1]，所以新的X射线相衬成像技术能够获得轻元素物质的高对比度图像．轻元素物质的种类很多，既包括碳纤维、光纤和有机材料，也包括生物软组织及其所组成的器官等．因此，X射线相衬成像技术可广泛用于材料科学、生命科学和医学等基础研究领域，开展工业无损检测、安全检查、生物医学成像和生物考古等方面的应用[2-5]．

近几十年来，X射线相衬成像技术已经发展了多种方法，主要可分为晶体干涉法、衍射增强法、同轴相衬和光栅相衬法4大类[6-9]．其中，光栅相衬法突破了对高相干X射线源的依赖，可用普通 X射线源实现，最有可能走向实际应用[10]．近年来，在众多研究小组的推动下，光栅相衬成像技术取得巨大进展．文献[11-12]开发了一台X射线光栅相衬成像原型机，开展人体关节炎疾病的实验研究，但其成像视场只能达到6 cm×6 cm．Stampanoni等[4]利用X射线光栅相衬成像装置开展了针对人体乳腺组织标本的实验研究，从其散射像中观察到了常规乳腺机无法识别的微细结构．文献[13-14]在德国慕尼黑工业大学研制了一台小型的X射线光栅相衬CT装置，用于开展X射线相衬成像的应用研究．此外，美国威斯康星-麦迪逊大学、瑞士苏黎世大学和德国纽伦堡-埃尔兰根大学等机构[15-17]，以及国内多个院校的研究小组[18-26]也在各自实验室搭建了X射线光栅相衬成像系统，开展器件研制和数值计算等方面的工作．

尽管X射线光栅相衬成像技术取得了重大进展，但该成像技术在成像视场和X射线的使用能量以及成像时间和辐射剂量等方面仍然受限．如何获得X射线大视场相衬图像，是近年X射线光栅成像的研究重点之一．理论上，通过调整系统中相位光栅和分析光栅栅条方向间夹角使莫尔条纹周期接近无限大可以使莫尔条纹在视场内消失，再由相位步进法就可以从记录的多幅图像中解出物体的相衬图像信息．而实际实验中成像系统所得莫尔条纹周期很难调整到无限大，随着成像视场的扩大，它在大视场内不能完全消失，这种情况下相位步进法中的位移误差会对相衬成像造成很大影响，导致所得相衬图像受到条纹背景的干扰．Vincent等[27]虽然通过理论推导了理想条件下X射线光栅相衬成像的机械抖动误差表达式，但未针对大视场情况下由于机械误差引起的背景条纹干扰做深入分析．本研究提出一种针对X射线光栅相衬成像位移误差的数值分析方法，建立理论模型计算不同位移误差下的相衬成像结果，讨论位移误差对大视场相衬成像的影响，为获得大视场相衬图像提供理论参考．

1 成像原理

X射线光栅相衬成像的原理示意如图1．该成像系统包含3个光栅，即G0、 G1和G2， 分别称为源光栅、相位光栅和分析光栅，分别用p0、 p1和p2表示3个光栅的周期， l是G0与G1之间的距离， d是G1与G2之间的距离．X射线透过源光栅G0形成多个线阵列源，在线阵列X射线源照明下相位光栅G1在距离d处形成其自成像条纹，即泰伯-劳效应．由于相位光栅自成像条纹的周期一般仅有几μm，无法使用普通X射线面阵探测器来探测，于是引入一个自成像条纹周期相同的分析光栅G2， 当两者线条方向之间的夹角θ很小时，可以形成周期很大莫尔条纹，并可用探测器直接探测．这时，在相位光栅G1前放入一个物体使X射线波前发生扰动，进而会使莫尔条纹发生变形．

理论上，当调整两光栅G1和G2栅条方向之间的夹角θ接近0°时，莫尔条纹的周期扩展接近无限大而在视场内消失，这时在分析光栅G2的一个周期p2内等步长移动分析光栅使其处于不同相对位置xg处，探测器记录下相应位置处的图像强度，同理再把物体放入视场中进行同样的操作，就可以利用算法从多幅不同位置的图像强度中解出物体的相衬图像．而实际实验中莫尔条纹周期很难调整到无限大，它在大视场内不能完全消失，移动分析光栅G2在一个周期内不同位置xg处探测器记录的强度分布可表示为

图1 X射线光栅相衬成像原理示意图Fig.1 Schematic diagram of grating-based X-ray phase-contrast imaging

I(x,y,xg)=a0(x,y)+a1(x,y)×

(1)

其中， a0和a1分别是记录得到莫尔条纹的平均强度和强度振荡幅度； φ是由物体引起的莫尔条纹相移，其对比度可表示为ν=a1/a0． 用上标r和s分别表示放置物体前后的情形，则可得到物体相衬图像的计算公式为

△Φ(x,y)=

(2)

其中， Nps是相位步进的步数； Ir和Is分别表示放置物体前后的像面强度．

由于位移平台机械抖动的影响，相位步进过程中分析光栅G2的位置xg会出现随机误差．位置xg的随机分布满足正态分布，其均方差为δxg， 可设误差系数α为均方差δxg与光栅周期p2的比值,即

(3)

由式(1)至式(3)可见，相位步进过程中分析光栅G2的位移误差会引起探测强度的起伏，进而对相衬图像△Φ(x,y)的计算结果造成影响．

2 系统参数设计

采用半径分别为10和12 mm的两个聚苯乙烯小球作为成像物体．聚苯乙烯是轻元素材料，密度小，对X射线吸收弱，可视为弱吸收相位物质．按照文献[20]设计的成像系统参数，设计使用X射线波长λ=0.04 nm，源光栅G0、 相位光栅G1和分析光栅G2的周期p0、 p1和p2分别为42.0、5.6和3.0 μm．其中， G1为π相位光栅，相应的源光栅G0到相位光栅G1的距离l=1 470 mm，相位光栅G1到分析光栅G2的距离d=105 mm．

计算中设置成像系统的莫尔条纹对比度为0.2，调整光栅间的夹角θ使其周期扩展为20 mm，成像视场大小为54 mm×54 mm，则在成像视场范围内莫尔条纹仍可见．采用5步相位步进算法，数值计算在误差系数α取值分别为0.10、0.05、0.02和0.01时所得小球的相衬图像结果，由此分析不同位移误差对X射线光栅相衬成像的影响．

3 结果与讨论

当误差系数α取不同值时，数值计算所得两个小球的相衬图像如图2．其中，图2(a)至图2(d)对应的误差系数α取值分别为0.10、0.05、0.02和0.01，即对应位移误差分别为光栅周期p2的1/10、1/20、1/50和1/100，图2(e)对应的误差系数为0，即理想情况下的成像结果．从图2可见，位移误差会使两个小球的相衬图像产生明暗条纹的背景干扰．位移误差越大，相衬图像的条纹背景干扰越严重．图3是对应图2中不同线型处相衬图像信号的分布曲线图，其中△Φ是相衬图像信号．从图3曲线图可见，当位移误差为p2的1/10时，得到的相衬图像信息几乎被背景条纹所淹没，无法识别小球的边沿信息．当位移误差为p2的1/20时，得到的相衬图像仍被条纹背景严重干扰，只能依靠先验识别小球的边沿信息．当位移误差为p2的1/50时，条纹背景对相衬图像有一定干扰，但已经可以清晰地识别出小球的边沿信息．当位移误差为p2的1/100时，条纹背景对相衬图像的干扰已基本可以忽略不计，得到小球的边沿信号与理想情况下的几乎重合．由此可得，要获得背景均匀的大视场相衬图像，位移误差最好要控制在位移周期的1/100以下．

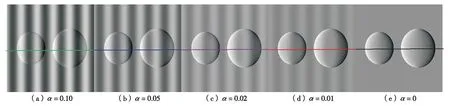
图2 误差系数取不同值时，两个小球的相衬图像Fig.2 Phase-contrast images of two spheres calculated with different shift errors

图3 不同位移误差下相衬图像信号的分布曲线图Fig.3 Curves in phase-contrast images calculated with different shift errors

出现上述结果，其原因是计算中成像系统莫尔条纹周期只有20 mm，它在54 mm×54 mm的视场内不能完全消失，这种情况下相位步进过程中的位移误差使莫尔条纹背景相位在放置小球前后发生了偏差．放置小球前，莫尔条纹的相位分布称为背景相位；放置小球后，X射线经过小球后的折射使莫尔条纹发生变化，莫尔条纹的相位分布由其背景相位和小球引起的变化相位叠加而成，理想情况下采用相位步进算法算出放置小球前后莫尔条纹的相位之差即可得到小球的相衬图像．但实际中由于机械振动引起相位步进过程中的位移误差，使放置小球后的莫尔条纹背景相位相对于放置小球前发生了偏差，采用式(2)的计算结果除了得到小球的相衬图像，还有位移误差引起的莫尔条纹背景相位偏差，由此导致小球相衬图像出现条纹背景的干扰．以误差系数α=0.10的情形进行说明，图4是当位移误差为分析光栅周期p2的1/10时，计算放置小球前后莫尔条纹的背景相位分布结果，图4中Φr和Φs分别是放置小球前后莫尔条纹的背景相位．从图4可以看到，在放置小球前后所得的莫尔条纹背景相位并不一致，相位偏差与位置坐标、位移误差大小都有关，所以由式(2)计算得到的小球相衬图像会出现明暗分布的条纹背景．可见，在进行X射线大视场相衬成像系统设计时，需着重考虑位移平台的机械抖动和重复定位精度，以保证相位步进过程中光栅的位置精度．

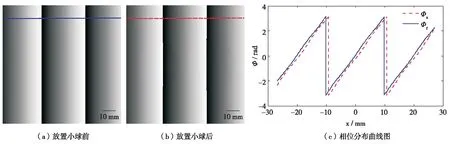
图4 放置小球前后莫尔条纹的背景相位分布图Fig.4 Background phase distributions of moiré fringes before and after placing the sphere

结 语

获取X射线大视场相衬图像，是X射线光栅相衬成像技术走向实用化需要解决的重要课题．由于实际实验中成像系统所得莫尔条纹周期很难调整到无限大，随着成像视场的扩大，它在大视场内不能完全消失，相位步进法中的位移误差使放置物体前后的莫尔条纹背景相位发生了偏差，导致由相位恢复算法计算得到的物体相衬图像出现明暗条纹的背景干扰，对相衬图像造成很大影响．本研究通过数值计算获得了不同位移误差下两个聚苯乙烯小球的相衬成像结果，从计算结果得到位移误差会使小球相衬图像产生明暗条纹的背景干扰，位移误差越大，相衬图像受背景条纹的干扰越严重．当位移误差达到位移周期的1/10时，小球相衬信息几乎被背景条纹所淹没，已无法识别其边沿信息．要获得背景均匀的大视场相衬图像，则位移误差最好控制在位移周期的1/100以下．本研究对位移误差的数值分析，将可作为X射线大视场相衬成像系统的设计重要参考，进而推动X射线相衬成像的实用化进程．

/ References：

[1] Henke B L, Gullikson E M, Davis J C, et al. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E=50-30 000 eV, Z=1-92[J]. Atomix Data and Nuclear Data Tables, 1993, 54(2):181-342.

[2] Donath T, Pfeiffer F, Bunk O, et al. Phase-contrast imaging and tomography at 60 keV using a conventional X-ray tube source[J]. Review of Scientific Instruments, 2009, 80:053701.

[3] Herzen J, Donath T, Pfeiffer F, et al. Quantitative phase-contrast tomography of a liquid phantom using a conventional X-ray tube source[J]. Optics Express, 2009, 17(12): 10010-10018.

[4] Stampanoni M, Wang Z, Thuring T, et al. The first analysis and clinical evaluation of native breast tissue using differential phase-contrast mammography[J]. Investigative Radiology, 2011, 46(12):801-806.

[5] Kottler C, David C, Pfeiffer F, et al. A two-directional approach for grating based differential phase contrast imaging using hard X-rays[J]. Optics Express, 2007, 15(3): 1175-1181.

[6] Bonse U, Hart M. An X-ray interferometer[J]. Applied Physics Letters, 1965, 6(8): 155-156.

[7] Davis T J, Gao D, Gureyev T E, et al. Phase-contrast imaging of weakly absorbing materials using hard X-rays[J]. Nature, 1995, 373:595-598.

[8] Wilkins S W, Gureyev T E, Gao D, et al. Phase-contrast imaging using polychromatic hard X-rays[J]. Nature, 1996, 384(6607): 335-338.

[9] David C, Nöhammer B, Solak H H, et al. Differential X-ray phase contrast imaging using a shearing interferometer[J]. Applied Physics Letters, 2002，81(17): 3287-3289.

[10] Pfeiffer F, Weitkamp T, Bunk O, et al. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources[J]. Nature Physics, 2006, 2: 258-261.

[11] Tannka J, Nagashima M, Kido K, et al. Cadaveric and in vivo human joint imaging based on differential phase contrast by X-ray Talbot-Lau interferometry[J]. Zeitschrift Für Medizinische Physik, 2012, 23(3): 222-227.

[12] Momose A, Yashiro W, Kido K, et al. X-ray phase imaging: from synchrotron to hospital[J]. Philosophical Transactions A: Mathematical Physical and Engineering Sciences, 2014, 372(2010): 20130023.

[13] Tapfer A, Bech M, Pauwels B, et al. Development of a prototype gantry system for preclinical X-ray phase-contrast computed tomography[J]. Medical Physics, 2011, 38(11): 5910-5915.

[14] Tapfer A, Bech M, Velroyen A, et al. Experimental results from a preclinical X-ray phase-contrast CT scanner[J]. Proceedings of the Nation Academy of Sciences of the United States of America, 2012, 109(39): 15691-15696.

[15] Zambelli J, Bevins N, Qi Z, et al. Radiation dose efficiency comparison between differential phase contrast CT and conventional CT[J]. Medical Physics, 2010, 37(6): 2473-2479.

[16] Revol V,Kottler C,Kaufmann R,et al.X-ray inter-ferometer with bent gratings: towards larger fields of view[J]. Nuclear Instruments and Methods in Physics Research A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 648(S1): S302-S305.

[17] Weber T, Bayer F, Haas W, et al. Energy-dependent visibility measurements, their simulation and optimisation of an X-ray Talbot-Lau interferometer[J]. Journal of Instrumentation, 2012, 7(11): 1313-1218.

[18] Huang Jianheng, Lei Yaohu, Du Yang, et al. Quantitative analysis of fringe visibility in grating-based X-ray phase-contrast imaging[J]. Journal of the Optical Society of America A: Optics, Image Science, and Vision, 2016, 33(1): 69-73.

[19] Liu X, Guo J C, Lei Y H, et al. Two-step phase retrieval method with unknown phase shift on non-absorbtion grating X-ray differential phase contrast imaging system[J]. Nuclear Instruments and Methods in Physics Research A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2012, 691:86-89.

[20] Lei Yaohu, Du Yang, Li Ji, et al. Application of Bi absorption gratings in grating-based X-ray phase contrast imaging[J]. Applied Physics Express, 2013, 6(11): 117301.

[21] Xi Yan, Zhao Jun. Inner-focusing reconstruction method for grating-based phase-contrast CT[J]. Optics Express, 2013, 21(5): 6224-6232.

[22] 刘 鑫，郭金川．部分相干光源微分相衬双图像相位恢复[J]．深圳大学学报理工版，2014，31(2)：169-173． Liu Xin, Guo Jinchuan. Dual-images phase retrieval in differential phase-contrast imaging with partial coherence source[J]. Journal of Shenzhen University Science and Engineering, 2014, 31(2): 169-173.(in Chinese)

[23] 李新斌，陈志强，张 丽，等．基于X射线光栅相衬成像的乳腺癌诊断技术的现状和发展前景[J]．中国体视学与图像分析，2015，20(4)：305-318． Li Xinbin, Chen Zhiqiang, Zhang Li, et al. The status and development prospect of the diagnosis of breast cancer based on grating-based X-ray phase-contrast imaging[J]. Chinese Journal of Stereology and Image Analysis, 2015, 20(24): 305-318.(in Chinese)

[24] 雷耀虎，刘 鑫，郭金川，等．超声对X射线分析光栅铋填充率影响研究[J]．深圳大学学报理工版，2016，33(2)：138-142． Lei Yaohu, Liu Xin, Guo Jinchuan, et al. Influence of ultrasonic on filling ratio of Bi in X-ray analyzer gratings[J]. Journal of Shenzhen University Science and Engineering, 2016，33(2):138-142.(in Chinese)

[25] Wang Shenghao,Olbinado M P,Momose A,et al.Experimental research on the feature of an X-ray Talbot-Lau interferometer versus tube accelerating voltage[J]. Chinese Physics B, 2015, 24(6): 673-678.

[26] 黄建衡，杜 杨，雷耀虎，等．硬X射线微分相衬成像的噪声特性分析[J]．物理学报，2014，63(16)：168702． Huang Jianheng, Du Yang, Lei Yaohu, et al. Noise analysis of hard X-ray differential phase contrast imaging[J]. Acta Physica Sinica, 2014, 63(16): 168702.(in Chinese)

[27] Vincent R, Christian K, Rolf K, et al. Noise analysis of grating-based X-ray differential phase contrast imaging[J]. Review of Scientific Instruments, 2010, 81: 073709.

【中文责编：英 子；英文责编：木 南】

Numerical analysis of shift error in X-ray phase contrast imaging for large field of view

Huang Jianheng1,2, Lei Yaohu1, Liu Xin1, Guo Jinchuan1, Li Ji1†, and Guo Baoping1

1) College of Optoelectronic Engineering, Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China 2) College of Information Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China

With the expansion of field of view (FOV) in grating-based X-ray phase-contrast imaging(XPCI), shift error in phase stepping method causes a great impact on the quality of phase-contrast image. A method is presented to analyze shift error in grating-based XPCI for large FOV, and the imaging results of two polystyrene spheres under different shift errors are obtained by numerical calculation. The results show that interferences of strip patterns appear in the background of phase-contrast images. The larger the shift error is, the more serious the interference becomes. When the shift error is up to 1/10 of the grating period, the edges of the spheres are unable to be identified from strip patterns. And shift error has to be set as less than 1/100 of the grating period to obtain a phase-contrast image without strip patterns for large FOV. The numerical analysis and discussion of shift error will be beneficial to the design of grating-based XPCI for large of view.

optical engineering; X-ray; phase-contrast imaging; phase stepping method; shift error; field of view

Received：2016-09-30；Accepted：2016-11-12

Foundation：National Special Foundation of China for Major Science Instrument (61227802); National Natural Science Foundation of China (11674232); China Postdoctoral Science Foundation (2016M592529)

† Corresponding author：Associcote professor Li Ji. E-mail: liji@szu.edu.cn

：Huang Jianheng, Lei Yaohu, Liu Xin, et al. Numerical analysis of shift error in X-ray phase contrast imaging for large field of view[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(1): 8-13.(in Chinese)

O 434.1

A

10.3724/SP.J.1249.2017.01008

国家重大科研仪器设备研制专项资助项目(61227802)；国家自然科学基金资助项目(11674232)；中国博士后科学基金资助项目(2016M592529)

黄建衡(1985—)，男，深圳大学博士后研究人员．研究方向：X射线光栅相衬成像系统和器件研究．E-mail：xianhuangjianheng@163.com

引 文：黄建衡，雷耀虎，刘 鑫，等．X射线大视场相衬成像位移误差的数值分析[J]. 深圳大学学报理工版，2017，34(1)：8-13.