点动图变思构图 分类探求寻突破——对一道九年级期末复习题的思路突破与感悟

沈岳夫（浙江省绍兴市柯桥区平水镇中学）

点动图变思构图 分类探求寻突破
——对一道九年级期末复习题的思路突破与感悟

沈岳夫（浙江省绍兴市柯桥区平水镇中学）

对一道以直角坐标系为依托，单动点为背景，融圆于一体的九年级期末复习综合题进行了深入的剖析.从它的来源、考查的重点、思路的突破，以及解法进行了详细的解读，总结、挖掘出一个常用的模型法，并进行推广，寻找出其内在的联系和规律.

解题教学；思路突破；拓展推广；教学启示

一、问题提出

在期末复习“圆的基本性质”等相关知识点时，笔者所选用的试卷中有下列一道压轴题．阅卷时笔者发现大多数学生留白，特别是第（3）小题留白现象最为严重，所教的两个班级中（76名学生）只有1名学生做得全对，不少学生无从下手，原因何在？故此，笔者静心下来，认真思考，如何引导学生走出解题困境呢？

题目如图1，在平面直角坐标系中，点M在x轴的正半轴上，⊙M交x轴于A，B两点，交y轴于C，D两点，且C为的中点，连接CE，AE，CB，EB，AE与y轴交于点F，已知A（-2，0），C（0，4）．

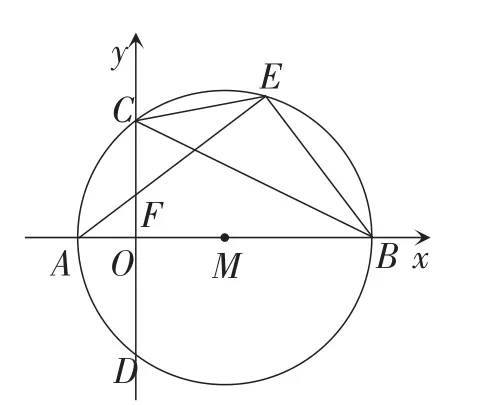
图1

（1）求证：AF=CF；

（2）求⊙M的半径及EB的长；

（3）如图2，P为x轴下方半圆弧上的一个动点，连接PE交CB于点R，当△CRE为等腰三角形时，直接写出EP的长．

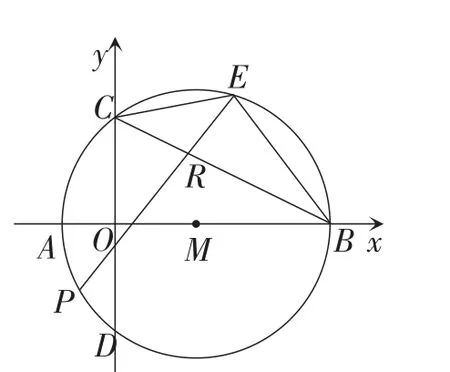
图2

此题源于2014学年第一学期浙江省慈溪市九年级期末考试数学试卷中的最后一题，此题是以直角坐标系为依托，单动点为背景，融圆于一体的综合题.从知识层面看，主要全面考查了垂径定理、勾股定理、等弧、圆周角、弦及其之间的关系，半径、弦心距、半弦之间的关系，全等三角形与相似三角形等知识点，这些知识都是初中数学的核心知识．从方法层面看，此题核心的解题方法是在直角坐标系下，利用上述基础知识，借助于转化思想、数形结合思想、模型思想、分类思想、方程思想等数学思想方法来解决有关问题．从经验层面看，解决此题需要学生具有一定的基本活动经验．从直角坐标系联想到∠COB=90°，且由C为的中点联想到圆周角、等弦等，进而联想到半径、弦心距、半弦之间的基本模型．但第（3）小题难度增大，颇具思维含量．其中题中的条件“当△CRE为等腰三角形”怎样构图是此题的难点，也是解决问题的关键．那么该题如何解？有何规律？

二、解题教学

数学家华罗庚谈到解题时说过，“退”到最原始的地方去，是解决问题的一个诀窍．最原始的地方，就是题干信息中的关键词：语句、点、线（段）、位置、运动、形的直观、数的直观、式的特征、形的对称等.它驱动着思维的起航，催生着解题思路的自然流淌，诠释并诉说着解法“是怎样想到的”．因此，就此题而言，由动点P产生的动线图形问题，需要分类思考，然后根据临界点位置分类画出符合要求的图形（最好是分离后的简化图形），这将为进一步突破思路提供了研究的平台．

1.重视审题

作为解题的第一个重要环节，审题往往得不到学生的充分重视．教师应以此为契机，引导学生认识到审题的必要性，通过举例说明两种常见题型的结构特征，即并列式与递进式（如图3）．

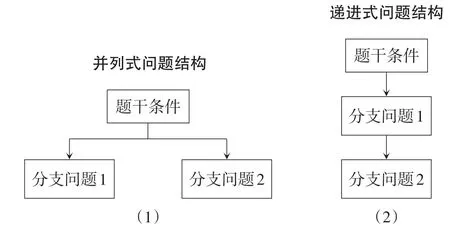
图3

2.追本溯源

仔细品味就会发现，构成这道试题的基本素材源于浙教版《义务教育教科书·数学》（以下统称“教材”）九年级上册第3章“圆的基本性质”．

（1）（教材第77页课内练习第1题）已知：如图4，在⊙O中，AB是⊙O的直径，OA⊥CD于点P．求证：

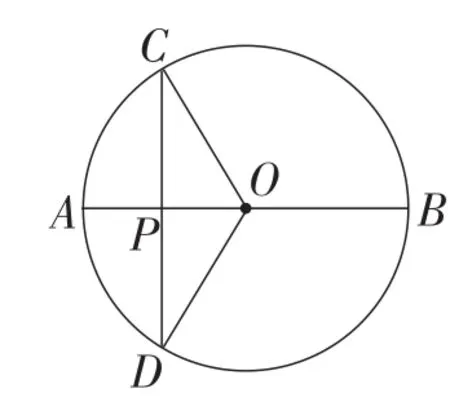
图4

（2）（教材第86页课内练习第2题）已知：如图5，在⊙O中，AB=CD．求证：AD=BC．

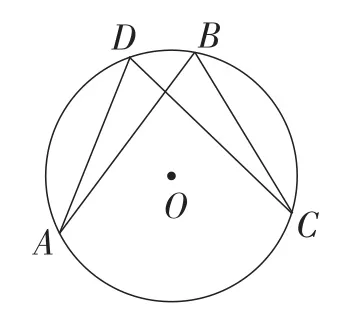
图5

（3）（教材第93页作业题第4题）已知：如图6，在⊙O中，AB=CD．求证：∠ABD=∠CDB．

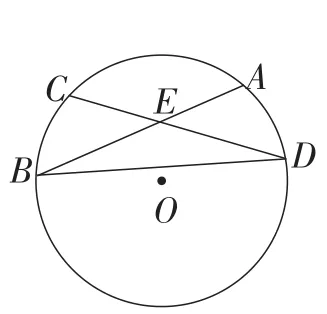
图6

命题者从教材习题的图形出发，抓住核心条件适当变式：一是将图4放到直角坐标系中，使显性条件隐性化；二是将图5、图6进行有机融合，将“静态”图形改为“动态”图形下“P为x轴下方半圆弧上的一个动点，连接PE交CB于点R，当△CRE为等腰三角形时，直接写出EP的长”的探索题，使问题得以延伸．

3.解法分析

提问1：探究圆中的问题时，方法选择的顺序是什么？

先考虑能否用圆的定理直接解决，再考虑转化为三角形问题来解决．

提问2：圆中的常用三角形有哪些？

用半径构造的等腰三角形，以半径（或直径）构造的半径、弦心距、半弦之间的直角三角形、全等三角形或相似三角形．

提问3：由直角坐标系想到什么？C为的中点联想到什么？

从直角坐标系联想到∠COB=90°，联想到垂径定理的基本图形；由C为的中点联想到圆周角、等弦，或垂径定理的逆定理等．

提问4：遇到动点问题，应注意什么？圆问题中求解线段长度问题的常用方法有哪些？

应注意分类讨论，画出符合题意的图形，以帮助分析解题；线段的和差关系、弧的和差转化为线段的和差关系、直角三角形的边角关系、相似三角形等，或单一使用，或组合使用．

解：（1）略；

（2）如图7，连接CM交AE于点G.

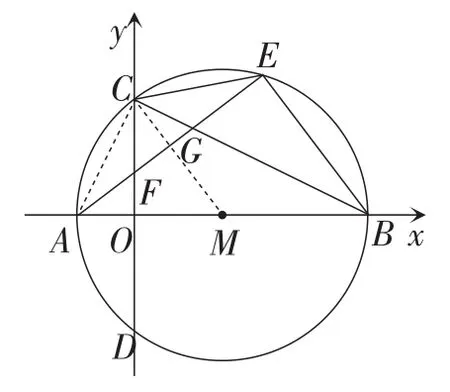
图7

设CM=x，则OM=x-2.

所以在Rt△COM中，求出x=5，

即⊙O的半径为5．

因为C为的中点，所以CM⊥AE，AG=GE．

易证△AOC≌△CGA.

所以AG=OC=4.

所以AE=8.

进而求得BE=6．

（3）当RC=RE时，如图8，此时∠REC=∠RCE，

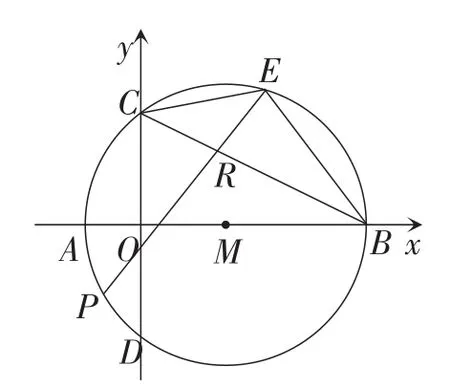
图8

所以EP=BC.

当CR=CE时，如图9，此时∠REC=∠ERC，

而∠REC=∠AEC+∠AEP，∠CRE=∠EBR+∠BEP，

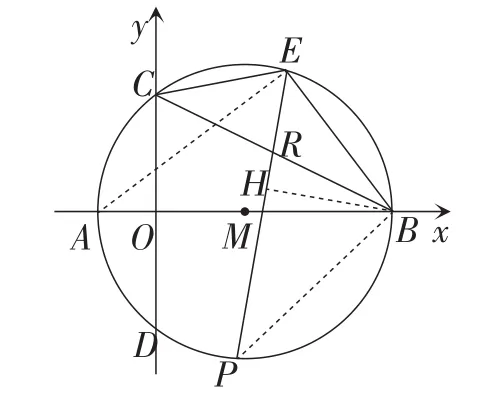
图9

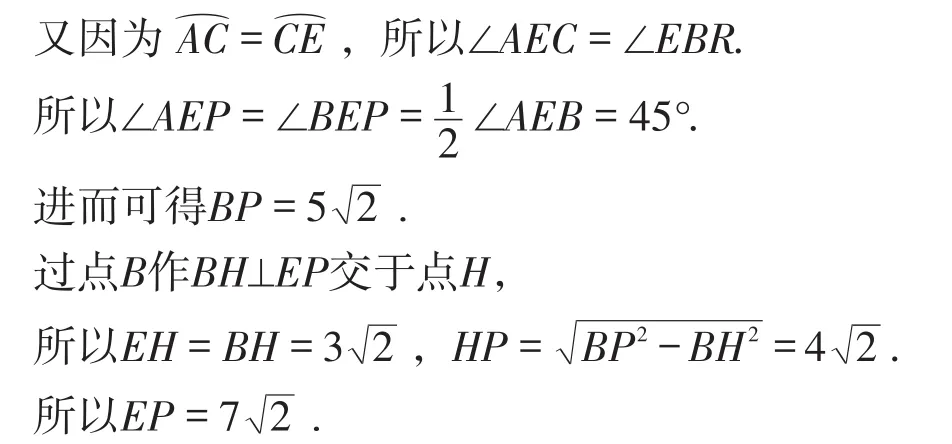
当EC=ER时，如图10，过点E作EH⊥CR交于点H，则易证△CEH∽△ABE.

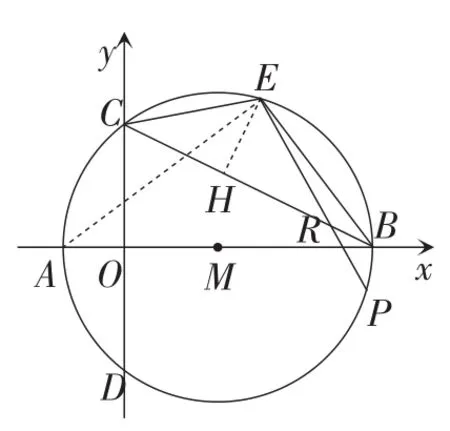
图10

所以EP=ER+RP=

综上分析，满足条件的EP长为或

【评注】对于第（2）小题应首先由C为的中点联想到垂径定理的逆定理，进而联想到垂径定理的基本模型，将求BE的长转化为求AE的长，而AE=2AG，然后由第（1）小题的暗示，可证△AOC≌△CGA，但这一点学生难以察觉，也就是学生的思维困境所在.对于第（3）小题设计了相互关联的问题，层次分明，难度增大，学生应对△CRE为等腰三角形进行分类讨论.当RC=RE时，由角相等EP=BC（这种方法笔者称之为“弧弦和差法”），这是对图5、图6的灵活运用；当CR=CE时，由角相等→∠REC=∠AEC+∠AEP和∠CRE=∠EBR+∠BEP（这种方法笔者称之为“底角转化法”，这是圆中证明等腰三角形的一种常用方法，应当引起重视）→∠AEP=∠BEP→特殊直角三角形，然后计算出线段长；当EC=ER时，应对题目细心观察，先添垂线EH，再由△CEH∽△ABE和“8字型”的△CER∽△PBR（这种方法笔者称之为“等腰添高相似法”），从而完成从已知向未知的过渡，将分散的条件通过两次相似等到等量关系，进而解决问题．

4.模型提炼

（1）提炼原题结论.

通过对CR=CE时的探求，我们进一步思考、猜想，可得到如下定理.

定理1：如图11，在Rt△ABC中，∠ACB=90°，⊙O为Rt△ABC的外接圆，CD平分∠ACB，且交⊙O于点D，则（AC＋BC）．

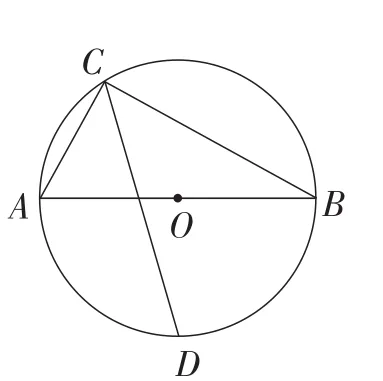
图11

（2）弱化一个条件（即∠ACB≠90°）.

把定理1的题设一般化：如果∠ACB≠90°，其他条件不变，那么AC，BC，CD这三者之间又有着怎样的数量关系呢？通过类比探究得到如下定理.

定理2：如图12，AC，BC是⊙O的两条弦，且∠ACB=θ，∠ACB的平分线交⊙O于点D，则AC+BC=

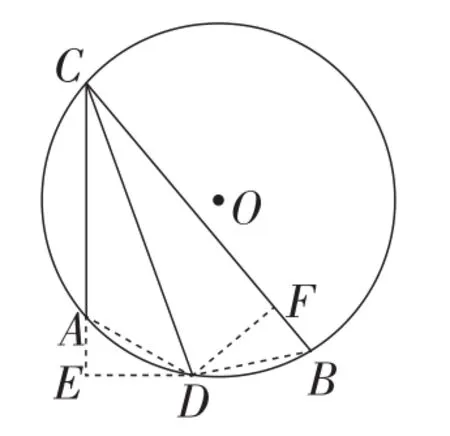
图12

证明：如图12，连接AD，BD，过点D作∠ACB两边的垂线DE和DF，垂足分别是点E，F．

可证Rt△ADE≌Rt△BDF.

得AE=BF.

则AC+BC=AC+CF+BF=AC+CF+AE=CE+ CF=2CE.

在Rt△CDE中，因为cos∠DCE=

所以CE=CDcos∠DCE，

【设计意图】通过对定理1、定理2的探究，揭示了命题中条件与隐含条件、结论的内在联系，为寻求解题途径指明了方向，使问题的解法简单流畅、别具一格，达到了化繁为简、化难为易的目的，而且还可以开拓学生的思路、提高解题能力，对学生的学习兴趣培养也大有裨益．

5.巩固提升

1．如图13，AB为⊙O的一固定直径，它把⊙O分成上、下两个半圆，过上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆（不包括A，B两点）上移动时，点P（ ）.

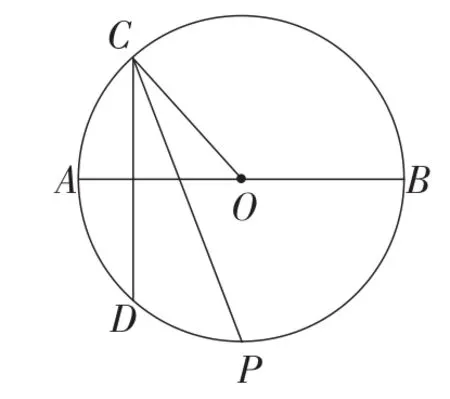
图13

（A）到CD的距离保持不变

（B）位置不变

（D）随点C的移动而移动

2．如图14，⊙O过四边形ABCD的四个顶点，已知∠ABC=90°，BD平分∠ABC，则：①AD=CD；②AB2+BC2=2CD2；③点O是∠ADC平分线上的点；④上述结论中正确的个数为（ ）.

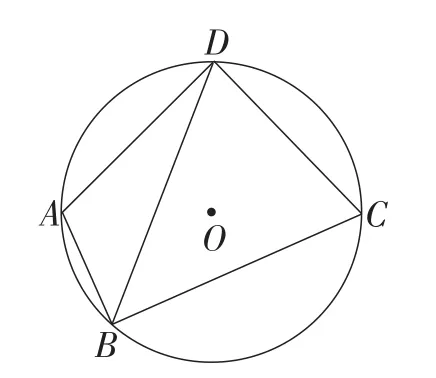
图14

（A）4 （B）3 （C）2 （D）1

3．如图15，半径为5的⊙O中，直径AB的不同侧有定点C和动点P，已知BC∶CA=4∶3，点P在上运动，过点C作CP的垂线，与PB的延长线交于点Q．

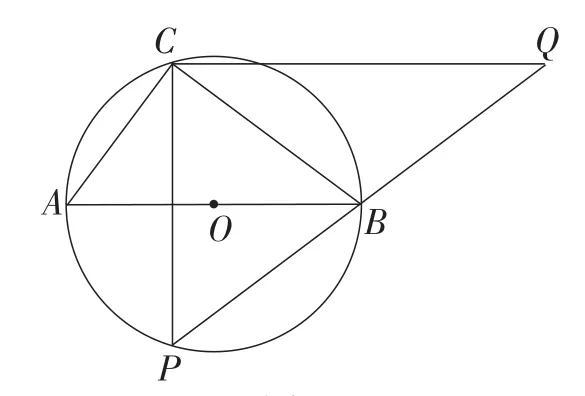
图15

（1）当点P与点C关于AB对称时，求CQ的长；

（2）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长；

（3）当点P运动到的中点时，求CQ的长.

4．如图16，在半径为5的⊙O中，弦AB=8，P是弦AB所对的优弧上的动点，连接AP，过点A作AP的垂线交射线PB于点C，当△PAB是等腰三角形时，线段BC的长为____________

．

图16

5．如图17，已知AB是⊙O的直径，AB＝8，点C在半径OA上（点C与点O，A不重合），过点C作AB的垂线交⊙O于点D，连接OD，过点B作OD的平行线交⊙O于点E、交射线CD于点F．

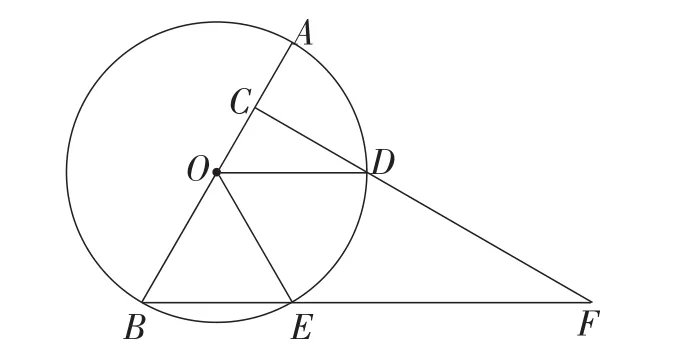
图17

（2）设线段OC=a，求线段BE和EF的长（用含a的代数式表示）；

（3）设点C关于直线OD的对称点为点P，若△PBE为等腰三角形，求OC的长．

【设计意图】设置5道巩固提升题，巩固深化对试题讲评的效果检验，前3道题侧重于角平分线的训练，后2道题侧重于动态分类讨论的巩固．目的在于学以致用，以满足不同层次学生的学习需求，力求使不同层次的学生在数学上得到不同的发展．

三、解后反思

1．关注思想方法，为学生提升素养蓄势储能

数学教学离不开数学思想方法，数学教学的核心是数学思想方法的渗透．《义务教育数学课程标准（2011年版）》提醒我们：数学思想蕴含在数学知识的形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象和概括．知识是能力的基础，能力是知识的升华，思想方法则是其灵魂．解决问题是对知识的运用，是学习经验的积累，是获得能力的途径.在解决问题的过程中，尤其要注重对数学思想方法的渗透与提炼.例如，分类讨论思想（如CR=CE或CR=CE或EC=ER进行分类）和转化思想（如构造出Rt△COM或Rt△CEH等）.除此以外，还需要用到数形结合、方程等思想方法．只有这样，才能培养学生发现问题和提出问题的能力，才能发展学生分析问题和解决问题的能力，数学思想是数学的精髓，它蕴含于数学知识的发生、发展和应用的过程之中．

2．立足构造图形，为学生分解难点铺路搭桥

解题难点是因人而异的，或源于解题者的知识漏洞，或源于发现不了隐含条件，或源于顾此失彼，等等．压轴题的区分功能意味着不同水平的学生都有得分空间．不强求全对，但要尽力，“分步、采点”不失为一种得分策略．利用图形思考、探究，有利于学生找到适合自己的解题方式．此题在探求△CRE为等腰三角形时特别注重了该方面的考查，尤其是第（3）小题根据动线PE，分类画出符合要求的图形（最好是分离后的简化图形，如图8～10），再细心观察，若能发现隐含信息，如∠REC=∠AEC+∠AEP和∠CRE=∠EBR+∠BEP，则能找到问题解决的突破口．上述当CR=CE或EC=ER时，若不借助图形的观察、分析是难以发现的．可见，有效构图，能使条件整合，能给予解题导向，能作为解题的监控工具，能为不同水平的学生各尽所能提供有利的条件．

3．重视变式训练，为学生思维升华拓展空间

著名的数学家希尔伯特说过，一个问题的解决意味着一系列新的问题的诞生．当我们解题成功时，不要忘记提出新的问题，因为还有许多宝藏尚未开发出来．教师解题不能局限于低效的就题论题的解题习惯，教师若能深入领悟典型题目的编写意图，进行“一题多法的探索，一题多问的发散，一题多变的尝试，多题归一的收敛，多题归一的提炼”的二度开发，这本身就是对解法之间的联系、解题方法的本质的深度挖掘，努力追溯问题背景及一般的结论（如上述提炼结论中的定理1和定理2等），臻于知其然的化境．经过这样的解题挖掘，解题内容就变得更丰富，习题形式变得更灵活，从而最大限度地彰显习题的价值，使习题教学从浅层走向深层、从单一走向多样；文中随着“巩固提升题”的逐一呈现，能够使学生懂其原理，知其方法，通其变化，这样学生在不知不觉中既解决了问题，又获得了方法，也提高了数学思维能力，让学生的解题学习由懂到会、由会到熟悉、由熟悉到巧．

［1］王静．一则教学片断的思考［J］．中学数学教学参考（中旬），2014（9）：33-34.

［2］桂文通．回归课本 提炼模型 推广命题［J］.中学数学（初中版），2014（12）：41-43.

［3］沈岳夫．以“本”为源巧建模 提炼规律妙解题：对一类函数视角下平行四边形顶点坐标求解的研究［J］．中国数学教育（初中版），2014（11）：43-47，64.

2016—09—14

沈岳夫（1963—），男，中学高级教师，主要从事初中数学教育教学和解题研究．