稀疏加权算法与GREIT算法在颅脑电阻抗成像中的对比研究

李昊庭，徐灿华，刘本源，杨琳，董秀珍，付峰

第四军医大学 生物医学工程系，陕西西安 710032

稀疏加权算法与GREIT算法在颅脑电阻抗成像中的对比研究

李昊庭，徐灿华，刘本源，杨琳，董秀珍，付峰

第四军医大学 生物医学工程系，陕西西安 710032

稀疏加权算法（L1算法）与GREIT算法是近年来两种较为热门的颅脑电阻抗成像（Electrical Impedance Tomography，EIT）图像重建优化算法，基于不同的数学模型，这两种算法性能不同。为了改善颅脑EIT重建图像质量并为其算法优选提供依据，本文基于三维颅脑仿真模型开展了仿真研究，对比了传统二阶范数加权算法（L2算法）、稀疏加权算法以及GREIT算法在颅脑电阻抗图像重建中的性能。仿真结果表明，相比传统二阶范数加权算法，两种优化的算法对颅脑EIT均有改善，而稀疏加权算法在图像噪声、形变误差、位置误差3项指标的评价中性能最优。在阈值函数的作用下，稀疏加权算法经多步迭代抑制了图像噪声，突出了重建目标。稀疏加权算法可以大大改善颅脑EIT效果，适用于颅脑EIT且对未来颅脑电阻抗重建算法扩展研究有重要参考价值。

颅脑电阻抗断层成像；动态成像；图像重建算法；算法比较；三维颅脑模型

引言

电阻抗成像（Electrical Impedance Tomography，EIT）技术的原理为通过安装在物体表面的电极对物体有规律地施加激励，若物体内部存在阻抗变化，则会引起表面测量电极电位的变化，基于测量电极电位变化，结合相应重建算法可以获得物体内部阻抗变化图像。EIT技术应用领域广泛，涉及肺功能成像，脑部功能成像，乳腺癌检测，腹部脏器功能成像等多个领域[1]。其中，颅脑电阻抗技术可以检测出脑功能性活动引起的阻抗变化，也可以检测出颅脑疾病如脑出血等引起的阻抗变化，具有诱人的应用前景[2]。

第四军医大学课题组长期致力于颅脑EIT研究，在国际上率先开展了颅脑EIT的临床实验研究，并取得了一系列的研究成果[3-4]。课题组研究发现相比实验室环境，临床实验中颅脑EIT面临更为严重的噪声与干扰。随机噪声、电极位移、接触阻抗的变化等多种因素均会影响到EIT的重建图像质量，故在临床实验背景下对重建算法的性能提出了更高的要求。在过去的几年中，围绕着提高重建图像质量和稳定性，国内外多个研究小组对重建算法开展了深入研究，在传统二阶范数加权算法（L2算法）的基础上提出了一系列优化算法。随着稀疏重建理论的发展，稀疏加权算法（L1算法）被应用到EIT，相比二阶范数加权算法，稀疏加权算法的抗噪声能力强，可以避免对重建图像边界造成过多模糊[5-7]。2009年Adler小组提出一种名为GREIT的优化算法并将其应用到肺部阻抗成像[8]。

基于简单仿真和部分实验研究，这些优化算法相对于传统算法，对EIT图像质量均有改善。然而，在颅脑EIT成像背景下针对这两种优化算法开展的算法比较工作尚未有文献报道。对此，本文基于三维颅脑仿真模型，模拟了EIT监测脑出血过程。我们在颅脑仿真模型不同位置设置了与血液电导率相同的球形目标，在添加一定的高斯噪声后，使用传统二阶范数加权算法、稀疏加权算法与GREIT算法进行图像重建，并基于图像噪声、位置误差、形变误差3项指标对重建结果进行了量化评价。根据重建图像与评价指标，我们总结了3种算法的不同特点并针对哪种算法更适合颅脑EIT进行了分析，为以后颅脑电阻抗算法的优选与优化打下了基础。

1 材料与方法

1.1 EIT算法原理

EIT算法可以分为正问题和逆问题求解。正问题指的是已知场域内部阻抗分布和边界条件，求解场域电势分布，其常用的求解方法为有限元方法[9]。逆问题又称作图像重建，则是给定边界测量数据和边界条件，求解场域内部阻抗分布。在EIT中，当场域内部阻抗变化较小时，边界测量数据与场域阻抗变化分布如下线性方程：

其中ρ表示场域电导率变化分布，v为边界测量数据，S是敏感系数矩阵。

由于EIT技术中测量数远远超过未知数，因此逆问题求解存在病态性，不能直接对（1）式求逆，采取的解决方法是引入正则项来构造如下的目标方程，然后求满足下式的最优解：

ρ^为阻抗变化分布的最优估计，λ为正则化参数，Φ(ρ)是正则化项。

1.2 常用的电阻抗重建算法

随着EIT算法的发展，形成了多种重建算法，不同算法具有不同的成像特点。本文选取了传统二阶范数加权算法、稀疏加权算法和GREIT算法3种常用的重建算法用于算法比较。

1.2.1 传统二阶范数加权算法

按照二阶范数正则化加权方法[10]，电阻抗目标函数有如下形式：

对于这种求二阶范数加权最优化问题，常用的阻尼最小二乘解[11]的形式为：

W为正则化矩阵，可以控制解的一些特性。

1.2.2 稀疏加权算法

按照稀疏重建理论，其目标函数如下：

由于一阶范数的存在，不能直接对上式进行求导，针对处理不可导项产生了一系列的稀疏加权算法，本文选取的是成像较好、收敛速度较快的SplitBregman算法（SB算法）[12]。

根据SplitBregman算法[13]，电导率分布可以按照以下3个步骤迭代求解：

其中(6)为二阶范数优化问题通过求导可得：

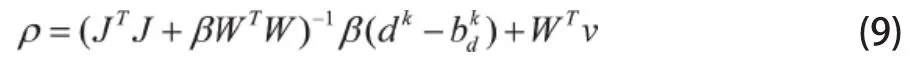
(7)为L1正则问题，可通过软阈值算子策略进行求解

其中Shrink为软阈值算子

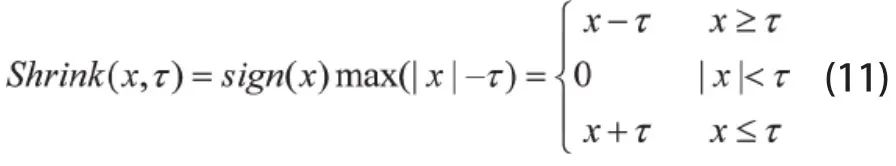
1.2.3 GREIT算法

EIT线性算法一般满足如下形式：

其中x为所求电导率分布，y为边界电位变化，R为重构矩阵。为了寻取最优的重构矩阵R，GREIT算法首先定义一系列的训练目标t(i)，然后寻求使下式误差最小的R作为优化的重构矩阵：

对于每一个训练目标，均可以生成与之对应的边界电位y和理想的重构值分布x。w是加权矩阵，代表训练目标集合t中每一个目标的权重。

对上式进行求导：

由上式，重构矩阵R为：

已知训练目标集合t与理想重构分布x、边界电位y满足如下关系：

D为训练目标集合与理想重构分布之间的映射矩阵，J为敏感系数矩阵，将上述两个 式子带入

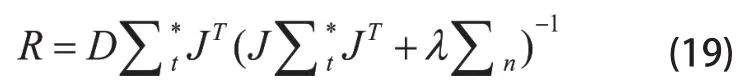
由(19)可知，相比传统算法，GREIT算法的核心在于映射矩阵D。D的作用为使训练目标集合t可以映射到符合EIT特点且均匀性较好的理想重构分布x。

1.3 三维真实颅脑仿真模型构建

基于Mimics软件对颅脑CT进行分割和三维表面重建，然后使用SolidWorks对三维表面模型实体转换，将实体化的模型导入Comsol4.4生成可用于颅脑EIT分析的有限元模型[14-15]，见图1。构建出的模型结构完整，包括头皮层、颅骨、脑脊液、脑实质以及脑室，见图2。

图1 病人颅脑CT图像

图2 导入Comsol后生成的三维有限元模型

分别对不同组织赋予不同的电导率[16]，基于该模型，可以较为真实的模拟颅脑疾病及颅脑电阻抗技术应用过程。

1.4 仿真实验设计

1.4.1 真实颅脑边界重构模板

选取电极所在平面对三维模型进行切割，导出切割面。手动选取中心点与边界点，然后对颅脑切面图进行自适应剖分，生成重构模板，见图3。

图3 真实颅脑边界重构模板

1.4.2 图像评价指标

我们参考了Adler等在2009年提出的算法评价指标体系并使用图像噪声（Image Noise，IN）、位置误差（Location Error，LE）、形变误差（Shape Error，SE）3项指标对重建图像进行评价。首先，定义重建图像中单元像素值大于最大像素值四分之一的集合为感兴趣区域集合，记作ΩROI，感兴趣区域以外的区域为Ωother。

dPre为参考图像中预设目标距离中心点的距离，dRe为重建图像重建目标距离中心点的距离，l为颅脑长轴长度，LE越小位置误差越小。

2 结果

首先使用简单圆域模型，在理想条件下进行仿真。在Comsol中构建圆域模型，圆域半径为0.2，背景电导率为1，见图4(a)。在圆域1/2处设置电导率为1.2，半径为0.01的圆形目标，生成边界电位数据后分别使用L2加权算法、L1-SB算法、GREIT算法进行图像重建，见图4。

图4 基于简单圆域的仿真实验结果

由图4简单圆域仿真结果可知，理想情况下，3种重建算法均能获得质量较好的重建图像，可以对目标准确定位。但由重建图像对应的扩散函数来看，3种算法重建特征存在较大差异。稀疏重建算法扩散函数在背景处几乎为0，而在目标边界处变化极为剧烈，对应的重建图像背景伪影少，重建目标边界明确；GREIT算法在目标内部扩散函数变化平缓，对应的重建目标较为均匀。

然后基于三维真实颅脑模型，进行仿真。分别在脑实质不同位置设置体积为5 cm3，电导率为0.7 Ω/m的球形目标模拟脑出血，并在生成的重建数据中添加0.1%的高斯噪声，使用L2算法、稀疏加权算法、GREIT算法进行图像重建，见图5。

由图5重建结果可知，相比理想重构， 基于颅脑三维仿真模型并添加高斯噪声生成的数据经重建后图像出现了扰动与伪影，尤其是在中心处的目标发生了较大的形变。对于3种算法的重建结果，传统L2加权算法获取的重建图像质量低于另外两种优化的算法；L1-SB算法对应的图像伪影最少，目标形变也较小；GRETI重建目标均匀性好。

图5 基于三维真实颅脑模型的仿真结果

与重建图像结果对应，在图像噪声、位置误差和形状误差三项指标上，稀疏加权算法的性能要优于其他两种算法，见图6。

3 讨论

本文在颅脑EIT应用背景下，基于三维颅脑仿真模型比较了传统二阶加权算法、稀疏加权算法与GREIT算法的性能。根据仿真实验结果可知，相比于传统的二阶范数加权算法，两种优化的算法对颅脑电阻抗图像重建均有一定的改善作用，但是基于不同的数学模型，两者的重建特性不同。稀疏重建算法的突出特点为抗噪性能好，可以保留边界，抑制由重建带来的形状误差，但是相比其他两种算法稀疏重建算法的需要调节的参数较多，在实际使用中增加了调参的负担[17]；而GREIT算法在加权矩阵D的作用下其解分布比较均匀，噪声相对较少。对于颅脑EIT成像，相比均匀性，抑制伪影与减少目标形变对于临床应用更为重要，故我们认为稀疏加权重建算法更适用于颅脑EIT。

另外，我们的对比研究中存在几点需要进一步完善的地方。首先，本文所有的参数选择均为手动选择，基于该方法选取的参数可能不是最优。但只要保证3种算法进行重建时采用的参数相同，算法对比工作就不会受到本质影响。其次，本文在仿真模型上验证了算法的性能，下一步我们将开展物理模型实验、活体实验来验证算法性能。

图6 图像重建误差堆状图

[1] 徐灿华,董秀珍.生物电阻抗断层成像技术及其临床研究进展[J].高电压技术,2014,40(12):3738-3745.

[2] Brown BH,Barber DC,Seagar AD.Applied potential tomography: possible clinical applications[J].Clin Phys Physiol Meas,1985,6 (2):109-121.

[3] Fu F,Li B,Dai M,et al.Use of electrical impedance tomography to monitor regional cerebral edema during clinical dehydration treatment[J].PloS One,2014,9(12):0113202.

[4] Dai M,Li B,Hu S,et al.In vivo imaging of twist drill drainage for subdura l hematoma: a clinical feasibility study on electrical impedance tomography for measuring intracranial bleeding in humans[J].PLoS One,2013,8(1):055020.

[5] Borsic A,Graham BM,Adler A,et al.Total Variation Regularization in Electrical Impedance Tomography[J].Inverse Probl, 2007,99(A12):A12.

[6] 范文茹,王化祥,郝魁红,等.基于两步迭代TV正则化的电阻抗图像重建算法[J].仪器仪表学报,2012,33(3):625-630.

[7] 常甜甜,魏雯婷,丛伟杰,等.电阻抗成像的稀疏重建算法[J].西安邮电学院学报,2013,18(2):92-96,110.

[8] Adler A,Arnold J H,Bayford R,et al.GREIT: a unif ed approach to 2D linear EIT reconstruction of lung images[J].Physiol Meas, 2009,30(6):S35-S55.

[9] Murai T,Kagawa Y.Electrical impedance computed tomography based on a finite element model[J].IEEE Trans Biomed Eng, 1985,(3):177-184.

[10] Lukaschewitsch M,Maass P,Pidcock M.Tikhonov regularization for electrical impedance tomography on unbounded domains[J]. Inverse Probl,2003,19(3):585.

[11] 徐灿华.床旁电阻抗动态图像监测的重构算法及实验研究[D].西安:第四军医大学,2010.

[12] Zhou Z,Dos Santos GS,Dowrick T,et al.Comparison of total variation algorithms for electrical impedance tomography[J]. Physiol Meas,2015,36(6):1193.

[13] Wang J,Ma J,Han B,et al.Split Bregman iterative algorithm for sparse reconstruction of electrical impedance tomography[J]. Signal Process,2012,92(12):2952-2961.

[14] 梁乐,徐灿华,沈志鹏,等.用于生物电磁场分析的脑部三层有限元模型构建[J].医疗卫生装备,2014,35(9):12-14.

[15] Markus J,James A,Emma M,et al.Correcting electrode modelling errors in EIT on realistic 3D head models[J].Physiol Meas,2015,36(12):2423.

[16] Tang C,You F,Cheng G,et al.Correlation between structure and resistivity variations of the live human skull[J].IEEE Trans Biomed Eng,2008,55(9):2286-2292.

[17] Tehrani JN,McEwan A,Jin C,et al.L1 regularization method in electrical im pedance tomography by using the L1-curve (Pareto frontier curve)[J].Appl Math Model,2012,36(3):1095-1105.

Comparative Study on the Application of Sparse Constrained Algorithm and GREIT in Brain Electrical Impedance Tomography

LI Hao-ting, XU Can-hua, LIU Ben-yuan, YANG Lin, DONG Xiu-zhen, FU Feng
Faculty of Biomedical Engineering, the Forth Military Medical University, Xi'an Shaanxi 710032, China

Sparse constrained and GREIT algorithms were two hot optimized reconstruction algorithms for brain Electrical Impedance Tomography (EIT). With different mathematical models, these two algorithms had different performances. To give recommendations to brain EIT algorithm selection, based on the three dimensional head model, a comparison of the performances of conventional quadratic norm regularization algorithm (L2 algorithm), sparse constrained algorithm and GREIT algorithm was made in this paper. On the basis of evaluation results, it could be concluded that sparse constrained algorithm and GREIT demonstrated better performances than L2 algorithm in image noise, location error and shape error. With threshold function, the sparse constrained algorithm suppressed the image noise by multi-step iteration, and highlighted the reconstruction object. Sparse constrained algorithm could greatly improve the performances of brain EIT and was suitable for brain EIT, which was of great reference for the researches on the brain EIT reconstruction algorithm EIT in the future.

brain electrical impedance tomography; dynamic imaging; reconstruction algorithm; algorithm comparison; three dimensional head model

R318；TM934.7

A

10.3969/j.issn.1674-1633.2016.11.005

1674-1633(2016)11-0023-05

2016-09-28

2016-10-10

国家自然科学基金（51477176）；军队重大课题（AWS14C006）。

付峰，教授，主要研究方向生物医学电阻抗成像。

通讯作者邮箱：fengfu@fmmu.edu.cn