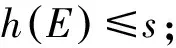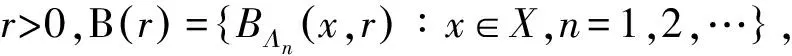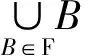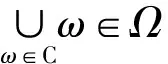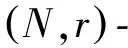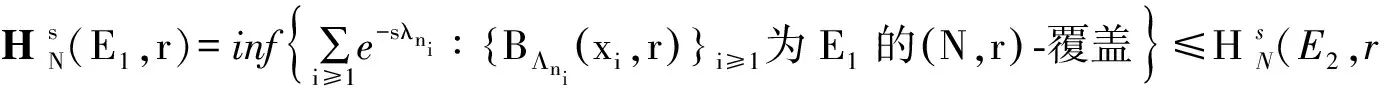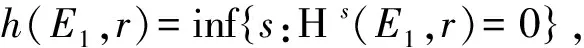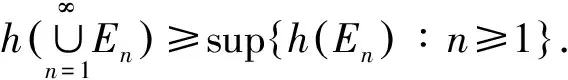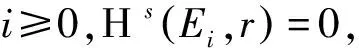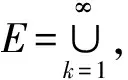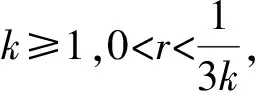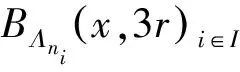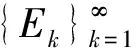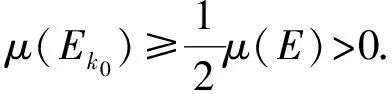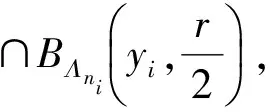d-作用下的Bowen拓扑熵理论

周 发

(合肥工业大学数学学院, 合肥230009)



周 发

(合肥工业大学数学学院, 合肥230009)

在d-作用下定义了Bowen维数熵,研究了d-作用下Bowen维数熵的一些性质,证明了X中的任意子集的Bowen维数熵可以通过该子集中的点的测度下局部熵估计.

Bowen维数熵； 测度下局部熵； 覆盖

1 引 言

熵是动力系统研究中的一个重要概念,测度空间上的熵的概念是由Kolmogorow在1958为解决遍历论中“是否存在两个具有连续谱的谱等价保测系统不是测度同构的”这一著名问题给出的.之后Adler等人于1965年在拓扑动力系统中用开覆盖对紧拓扑空间上的连续自映射定义了拓扑熵.1971年Bowen引入张成集和分离集来定义拓扑熵,并且验证了当空间为紧度量空间时此拓扑熵与Adler等人定义的拓扑熵一致.我们知道虽然用张成集和分离集定义的拓扑熵比用开覆盖定义的拓扑熵更具有实用性,但两者都存在一定的局限性.用开覆盖定义的拓扑熵只能定义映射在整个紧拓扑空间上的拓扑熵,张成集和分离集定义的拓扑熵虽然应用广泛,但是只能定义紧子集和整个空间上的拓扑熵.后来Bowen又在1973年借鉴几何测度论中关于Hausdorff维数的定义(见文献[2]),给出了非紧空间上拓扑熵的定义(这种熵又被称为Bowen维数熵),Bowen进一步研究其性质,证明了全空间上的Bowen维数熵与通常定义的拓扑熵是相等的.

在分形几何中,分形维数是描述分形集合的一个重要工具,一般我们可以借助全空间上支撑的测度下局部维数来估计集合的Hausdorff维数.在拓扑动力系统中我们也可以做类似的研究,文献[1]的作者借助非紧空间上的点的测度下局部熵来估计系统子集的Bowen维数熵.但需要说明的是,上述研究大多针对的是整数加群或自然数半群作用.

一个自然的问题就是,对与其他的群是否有类似的结果.本文将在文献[1]的基础上,进一步研究在一类特殊的群作用(d-作用)下Bowen维数熵的性质及X的任意子集的Bowen维数熵能否由X子集中的点的测度下局部熵来估计.

2 定 义

定义2.1设(X,d)是一个紧度量空间,一族连续的变换T∶={Th∶X→X}h∈L被称作为连续的L-作用,其中L=d或如果T满足

(i) Th+k=Th∘Tk(h,k∈L)； (ii)T0是恒同映射.

对k∈L且Λ⊂L,令集合Λ+k={h+k:h∈Λ}.对n∈+令

且λ=#Λn,其中#Λn代表集合Λn中元素的个数(见文献[3]).

设(X,d)是一个紧度量空间,T为连续的L-作用,其中L=d或对任意n∈,x,y∈X,r>0,定义

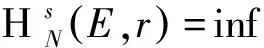
定义2.3设μ是X上的Borel概率测度,称

为关于μ在x∈X处的测度下局部熵.

3 主要结果及证明

定理3.1设μ是X上的Borel概率测度,E是X上的Borel子集,且0

(ii) 若hμ(x)≥s对所有的x∈E成立,且μ(E)>0则h(E)≥s.

在证明定理3.1之前,首先证明三个引理.引理1的证明类似于传统的5r覆盖定理(见文献[1],定理2.1).

且G中的元素两两不相交.

证令ω⊂F为满足以下条件的集族：

(i) B1≠B2∈ω得B1∩B2=∅；

引理2设(X,d)是紧致度量空间,T为连续的L-作用,L为d或且E1⊂E2⊂X,则).

引理3设(X,d)是紧致度量空间,T为连续的L-作用,L为d或且En⊂X,n≥1,则

对所有的j≥1成立.所以对任意的N≥1,有Ek⊂F,其中

当N→∞时,

结合引理3可得

由ε的任意性知,h(E)≤s.

(ii) 对任意的ε>0,对任意的k≥1,令

可以得到

因此,当N>N*时有

结合定义2.2知

令r→0得

h(E*)≥s-ε.

由引理2知h(E)≥h(E*)≥s-ε,由ε的任意性知h(E)≥ε.

[1] Ma J and Wen Z.A Billingsley type theorem for Bowen entropy[J].C R Acad Sci Paris, 2008, 346:503-507.

[2] Bowen R.Topological entropy for non compact sets[J] .Tans Amer Math Soc, 1973,184:125-136.

[3] Yamamoto K.Topological Pressure of the set of generic points fordactions[J].Kyushu J Math, 2009 , 63: 191-208.

[4] Federer H.Geometric Measure Theory[M].New York :Springer-Verlag, 1969.

[5] Mattilla P.Geometry of Sets and Measures in Euclidean Spaces[M].Cambridge：Cambridge University Press, 1995.

On Bowen Dimension Entropy of Dynamical Systems ofdAction

ZHOUFa

(Department of Mathematics, Hefei University of Technology, Hefei 230009, China)

We introduce the notion of Bowen dimension entropy fordynamical systems ofdactions for non compact sets, and we study its properties, moreover, we proved that the Bowen dimension entropy of a subset can be estimated by the lower measure local entropy of the points in this set.

Bowen entropy; lower local entropy; cover

2016-05-17； [修改日期] 2016-06-22

国家自然科学基金(11001071，11171320)；中央高校基本科研业务费(2015HGZX0017)

周发(1992-),男,硕士研究生,从事动力系统研究.Email：1287218528@qq.com

O192

A

1672-1454(2016)06-0013-05