由粗到细的图像浅浮雕生成算法
吴文明, 刘利刚
(中国科学技术大学数学科学学院,合肥230023)
由粗到细的图像浅浮雕生成算法
吴文明, 刘利刚
(中国科学技术大学数学科学学院,合肥230023)
针对现有基于三维场景的浅浮雕生成算法输入要求高等问题,提出了一种基于图像的细节增强的浅浮雕生成算法.首先由图像的灰度值提取高度场,通过对高度场的光滑处理得到浮雕的大致轮廓.然后对图像进行细节增强处理,提取图像的细节部分.最后将细节部分转化为高度场,并与上述光滑浮雕相互叠加,得到细节增强的浅浮雕模型.该算法的输入要求低,简单易于实现.实验表明算法能够利用图像生成细节增强的浅浮雕,具有实用价值.
数字浮雕; 网格光滑; 细节增强; 边缘检测
1 引 言
浮雕是雕刻艺术的一种,通过压缩三维场景的整体深度,再将压缩后的三维场景以平面或者其他光滑曲面为载体雕刻出来,得到一种介于三维雕刻和平面绘画之间的独特艺术效果.而浅浮雕是通过对三维场景的高度压缩,利用立体透视和错觉等手法表现出场景的立体感和空间感.
传统的浮雕创作主要依靠手工,这要求技师掌握专业的雕刻技术和艺术创作经验.即便如此,纯手工的浮雕创作依然是一项耗时耗材的工作,后续的编辑和修改也具有一定的难度.随着信息技术的发展和3D打印技术[1]的普及,数字浮雕技术[2]应运而生.数字浮雕技术利用计算机进行浮雕设计,大大提高了浮雕的设计效率和制作精度,设计者不需要掌握相关的专业知识就可以设计个性化浮雕,也可以随时修改和编辑浮雕.
近年来涌现出很多数字浮雕相关的研究工作.随着三维数据获取技术的广泛应用,研究比较多的工作是对三维场景在给定视觉方向上进行深度压缩生成浮雕.主要有两类方法:基于高度场直接压缩生成浅浮雕[3,4]和基于梯度场压缩的数字浮雕设计[5,6,7].这些方法往往需要用户提供场景的三维信息,对用户的输入要求比较高,而普通用户接触到的数据大多数是二维的,比如照片.还有一类研究工作是基于二维图像生成浅浮雕.主要思想是将图像的灰度值转化为三维深度信息,最后获得三维的浮雕模型[8,9,10].这与计算机图形学中的Shape-from-Shading方法[11,12,13]类似.如[12]利用Shape-from-Shading方法生成基于二维图像的浅浮雕模型,模型在给定光照下通过表面漫反射形成图像的效果.基于图像的浅浮雕算法由于输入简单,具有实用价值.目前这类方法已经在一些商业软件中得到应用,如ArtCAM.但是这类方法具有明显的缺点.一方面,图像的灰度信息不能准确恢复场景的深度信息,离散的灰度信息也会导致浮雕具有噪音;另一方面,图像本身的噪音导致最终生成的浮雕与期望的效果产生偏差,细节和特征丢失严重.
本文提出一种基于图像的由粗到细的浮雕生成算法.第一步,将输入图像转化为高度场,再对高度场进行光滑处理得到浮雕的大致轮廓.第二步,对输入图像进行去噪、细节增强等处理,再提取图像的高频信息得到浮雕的细节.最后融合上面两步的结果,得到细节增强的浅浮雕模型.
2 主要算法
算法以二维图像作为输入,输出为图像对应的细节增强的浅浮雕模型.算法的具体细节将在下文中阐述,算法流程如图1所示:

图1 基于图像的浅浮雕生成算法
2.1 粗糙浮雕生成
2.1.1 高度场提取
首先将图像转化为高度场,这一步也直接影响最终的浮雕效果.然而在没有其他先验信息的情况下找到灰度值与真实场景深度的对应关系是非常困难的.因此,本文假设:灰度图是由于光线透过浮雕形成的,光通过不同的厚度产生不同的灰度值.本文将透光作为先验信息,以此推导出灰度值与真实场景深度的对应关系.从这个观点看,基于图像的浮雕生成实际上是一种逆向工程.
设灰度图上每点的灰度值为I(x,y),取值范围是[0,255],其中(x,y)表示像素点的位置坐标.设浮雕在(x,y)处的深度为H(x,y).要建立I(x,y)和H(x,y)之间的映射H:
H(x,y)=H(I(x,y)).
根据布朗-朗伯定律,光经过一定介质后的出射光强为
I=I0e-αh,
(1)
其中I0表示入射光强,h表示光束垂直通过介质层的厚度,α为介质对光的吸收系数.
由(1)式得
(2)
直接用灰度值代替(2)中的光强由此得到灰度值与真实场景深度的对应关系
(3)
其中I0表示初始灰度值,一般取为255.
考虑到当像素值为零或者接近于零的小数时,对数函数值将趋于无穷小,于是对灰度图的像素值作如下线性变换
(4)
设置浮雕的高度的取值范围是[σ1,σ2],则灰度值与浮雕高度的关系为
(5)
利用公式(5)将图像转化为高度场,如图2所示.由图可知,提取到的高度场存在大量噪音.

(a) 输入图像 (b) 由(a)提取的高度场 (c) 经过光滑处理的高度场图2 从图像中提取高度场
2.1.2 网格光滑
由于灰度离散的特点,提取的高度场具有比较突出的噪音,如图2(b)所示.因此需要对高度场进行去噪和光滑处理,同时尽可能保留浮雕的大致形状.关于网格去噪和光滑的研究一直是学术界的研究热点.本文采用[14]提出的网格去噪方法,该方法简单高效,并且能够保留原始的网格特征如尖锐的边和角,符合我们的要求.该方法主要包括两步.第一步,利用加权平均的邻域面片法向通过迭代的方式滤去含有噪音的面片法向,法向滤波函数为

其中FV(i)表示顶点V(i)的所有一邻域的三角面片集,n′k是面片Fk的单位法向,ck是面片Fk的中心.
带有噪音的网格经过去噪后的结果如图2(c)所示.由图可知,虽然光滑处理去掉了原始高度场的噪音,但是也丢失了细节和特征.
2.2 细节浮雕生成
2.2.1 细节增强
由于图像存在噪音以及特征不明显等问题,为了获取比较良好的细节信息,采用图像处理中的细节增强技术对图像进行适当处理,主要包括伽马校正、直方图均衡化以及高频滤波技术.
伽马校正由于输入图像整体色调偏暗,对比度不明显,因此需要对图像进行亮度调整,通过对不同的像素值设计适当的调整因子,使得图像中的深色和灰色部分以不同的比例增大,从而提高图像的对比度.伽马校正是传统显示设备为了显示真实的图像而提出的一种偏差矫正技术,通过调整图像的伽马曲线,能够有效地提高图像的对比度,在一定程度上增强图像的细节.
伽马校正的公式为
I′(x,y)=I(x,y)gamma(gamma>0).
当gamma>1时,图像的伽马曲线如图3(a)所示.由伽马曲线可知,低灰度值的像素点被赋予较大的调整因子,而高灰度值的像素点被赋予较小的调整因子,这样就导致图像的高光部分被压缩而暗调部分被扩展,图像整体偏暗;当gamma<1时,图像的伽马曲线如图3(b)所示.此时情况恰恰相反,图像的高光部分被压缩而暗调部分被扩展,图像整体偏亮.本文选择gamma=0.65以增加输入灰度图的亮度,同时提高图像的对比度.

(a) gamma>1 (b) gamma<1图3 伽马校正曲线
直方图均衡化在伽马校正的基础上,采用直方图均衡化的方法进一步增强图像的细节部分.直方图是指统计图像各灰度级像素的数量所得到的关于图像亮度信息的直方图,均衡化是指通过灰度映射获得灰度级分布均匀的直方图.直方图均衡化的结果是扩展了图像的动态范围,从而增强图像的整体对比度.
直方图均衡化[15]的灰度映射T可以表示为
其中Sk是均衡化后的第k级均衡化灰度,rk是均衡化前第k级灰度级,pr(rj)表示图像中第r级灰度出现的概率,rj表示归一化的灰度级,nj表示rj对应的像素数量,n表示原图像中的像素总数.
单纯的直方图均衡化是一种全局方法,在增加整体对比度的同时忽略了局部对比度.自适应的直方图均衡化则是通过计算图像的局部直方图,然后重新分布亮度来来改变图像对比度,因此更适合改进图像的局部对比度以获得更多的图像细节.
高频滤波为了进一步增强原始图像的对比度,突出特征和细节,通过高频滤波获得输入图像的高频信息,然后再和上述自适应直方图均衡化的结果相互叠加.高频滤波是在频率域进行的.因此需要考虑二维离散傅里叶变换
及逆变换
频域滤波[15]的基础是卷积定理
f(x,y)*h(h,y)⟺H(u,v)·F(u,v),
其中H(u,v)和F(u,v)分别表示h(h,y)和f(x,y)的傅里叶变换,符号“·”表示两个函数的乘法运算,符号“*”表示两个函数的卷积运算,定义如下

f(x,y)*h(h,y)构成空间域上的滤波,H(u,v)·F(u,v)构成频域上的滤波.根据卷积定理,傅里叶变换对的空间滤波等价于频域滤波.高频滤波是通过选择合理的滤波函数H(u,v)来减少F(u,v)的低频分量,保持高频分量相对不变,再通过傅里叶逆变换间接实现对输入图像f(x,y)的滤波操作.
本文选取的滤波函数为
其中(u0,v0)表示频率原点,d0为截至频率,本文取d0=10.为了去除图像中的噪音,直接忽略高频图像中像素值较小的点.将高频滤波的结果与上述自适应直方图均衡化的结果相互叠加,得到最终细节增强的图像.图像细节增强的流程如图4所示.

图4 细节增强的图像
2.2.1 细节提取
本节利用Sobel边缘检测算子提取图像细节,提取到的信息可以作为对粗糙浮雕丢失细节的补充,从而增强浮雕的细节效果.Sobel边缘检测算子分别计算上下和左右两组相邻像素间的灰度差,与之接近的像素点赋予较大权重,距离较远则赋予较小权重,最后两个方向的加权结果结合起来构成Sobel检测值.算法表示为
其中I表示待检测的图像.Sobel边缘检测算法包含横向及纵向两组检测算子,分别与图像作卷积得到横向及纵向的亮度差分近似值.最后将两个方向的结果结合起来得到Sobel检测值为
Sobel边缘检测算子简单易于实现,能够产生良好的边缘检测效果,同时对噪音具有平滑的作用,受噪音影响比较小.本文应用Sobel边缘检测算法,提取图像细节的结果如图5所示.

图5 利用Sobel算子提取细节
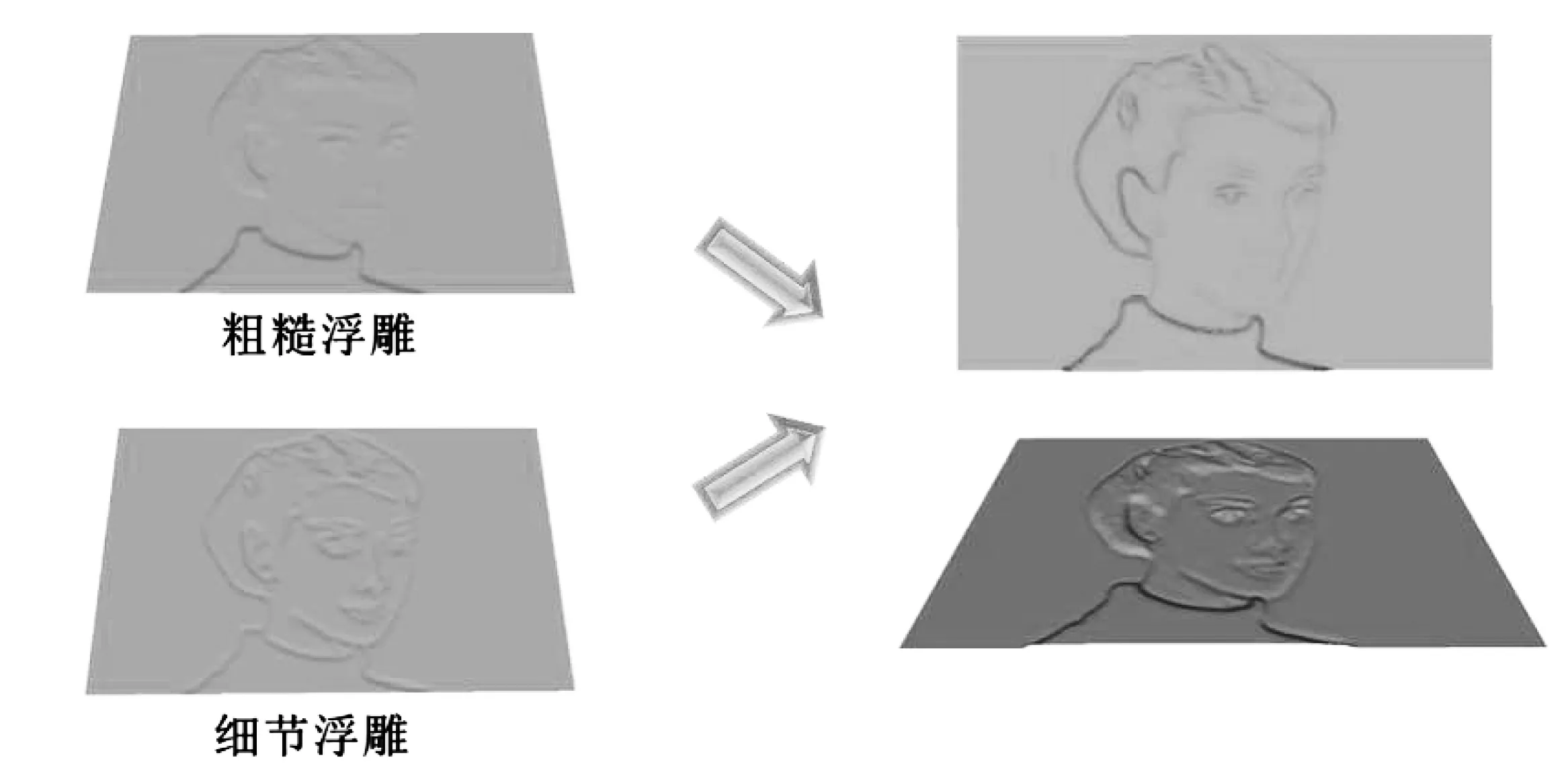
图6 细节增强的浅浮雕
利用公式(5)将提取到的细节信息转化为高度场,再与上文中的粗糙浮雕相互叠加.这样,浮雕的细节部分得到加强,同时保持非细节部分相对不变,得到最终细节增强的浅浮雕模型(图6).

图7 更多的浮雕结果
3 结 论
本文提出一种基于图像的细节增强的浅浮雕生成算法.算法主要分为两步:第一步,将输入图像转化为高度场,再对高度场进行光滑处理得到浮雕的大致轮廓.第二步,对输入图像进行去噪、细节增强等处理,再提取灰度图的高频信息得到浮雕的特征.最后通过融合第一步和第二步的结果,得到细节增强的浅浮雕模型.本文提出的浅浮雕设计算法以二维图像作为输入,对输入的要求较低;算法将去噪和细节增强分开处理,尽可能利用图像提供的信息增强生成浮雕的效果.本文的算法简单易于实现,实验结果表明本文算法能够通过灰度图生成细节增强的浅浮雕,具有实际应用价值.算法仍然存在一些问题值得继续研究,如何更好地提取细节信息,如何对提取的细节信息进行去噪以保证提取的细节质量等等.
[1] 刘心平, 温洋.精美绝伦的数字化浮雕艺术[J].美术大观, 2010 (10): 124-124.
[2] 刘利刚, 徐文鹏, 王伟明, 等.3D打印中的几何计算研究进展[J].计算机学报, 2015, 38(6): 1243-1267.
[3] Cignoni P, Montani C, Scopigno R.Computer-assisted generation of bas-and high-reliefs[J].Journal of graphics tools, 1997, 2(3): 15-28.
[4] Sun X, Rosin P L, Martin R R, et al.Bas-relief generation using adaptive histogram equalization[J].IEEE transactions on visualization and computer graphics, 2009, 15(4): 642-653.
[5] Weyrich T, Deng J, Barnes C, et al.Digital bas-relief from 3D scenes[C]∥ACM Transactions on Graphics (TOG).ACM, 2007, 26(3): 32.
[6] Kerber J, Tevs A, Belyaev A, et al.Feature sensitive bas relief generation[C]∥Shape Modeling and Applications, 2009.SMI 2009.IEEE International Conference on.IEEE, 2009: 148-154.
[7] Bian Z, Hu S M.Preserving detailed features in digital bas-relief making[J].Computer Aided Geometric Design, 2011, 28(4): 245-256.
[8] Pan M W J C J, Zhang J J.Image-based bas-relief generation with gradient operation[C]∥Proceedings of the 11th IASTED International Conference.2010, 679(040): 33.
[9] Zhang Y W, Zhou Y Q, Li X L, et al.Bas-Relief Generation and Shape Editing through Gradient-Based Mesh Deformation[J].Visualization and Computer Graphics, IEEE Transactions on, 2015, 21(3): 328-338.
[10] Wu J, Martin R R, Rosin P L, et al.Making bas-reliefs from photographs of human faces[J].Computer-Aided Design, 2013, 45(3): 671-682.
[11] Zhang R, Tsai P S , Cryer J E, et al.Shape from shading:a survey[J] .IEEE Transactions on Pattern Analysis And Machine Intelligence, 1999, 21(8) : 690-706.
[12] Alexa M, Matusik W.Reliefs as images[J].ACM Trans.Graph., 2010, 29(4): 60:1-60:7.
[13] Kolomenkin M, Leifman G, Shimshoni I, et al.Reconstruction of relief objects from line drawings[C]∥Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on.IEEE, 2011: 993-1000.
[14] Sun X, Rosin P, Martin R, et al.Fast and effective feature-preserving mesh denoising[J].IEEE transactions on visualization and computer graphics, 2007, 13(5): 925-938.
[15] 冈萨雷斯, 伍兹, 埃丁斯, 等.数字图像处理: MATLAB版[M].北京:电子工业出版社, 2005.
Course-to-fine Bas-relief Generation Algorithm from Images
WUWen-ming,LIULi-gang
(School of Mathematical Sciences, University of Science and Technology of China,Hefei 230026, China)
Current methods for generating digital bas-relief based on 3D scenes have high input requirements, this paper proposes a detail enhancement bas-relief generation algorithm based on the image.By the method, first we extract the height field based on the gray values of the image, and a rough shape of the bas-relief can be obtained by smoothing the height field.Then we apply some detail enhancement operations on the image and detect the details of the image.Finally, we turn the detail part into a detail height field and add it to the smooth height field to generate a detail enhancement bas-relief model.The approach has low input requirements as well as easy to implement for its simpleness.Experimental results show that the approach can be applied to generate detail enhancement bas-reliefs, which has practical value.
digital bas-relief; mesh smoothing; detail enhancement; edge detection
2016-09-30; [修改日期]2016-10-17
国家自然科学基金项目(61222206,11526212);中科院“百人”计划
吴文明(1992-),男,硕士在读,从事计算机图形学研究.E-mail:wwming@mail.ustc.edu.cn
TP391
A
1672-1454(2016)06-0001-07

