线性代数课程教学案例建设研究
文 军, 屈龙江, 易东云
(国防科学技术大学理学院,长沙410073)
线性代数课程教学案例建设研究
文 军, 屈龙江, 易东云
(国防科学技术大学理学院,长沙410073)
总结了国内外在线性代数课程教学案例上的探索,在对课程知识应用进行深入分析的基础上,对近年来案例建设的实践进行了系统的总结思考;通过对典型教学案例的分析,为进一步的工作准备了基础.
线性代数; 案例建设; 实践; 分析; 思考
1 引 言
线性代数课程以讨论有限维空间线性关系的理论和方法为主要教学内容,具有高度的抽象性,且概念多、符号多、定理和公式多,知识点相互渗透且应用灵活,此外当前教学往往强调数学知识体系的严谨性,通常用比较抽象的数学方法来描述普适性的规律,强调培养学生的抽象思维能力;而我校线性代数课程在大一的第一个学期开设,本科新生的数学知识与思维能力还限于中学阶段,并未完全具备严谨的抽象思维和推理技能,就会使学生对线性代数课程的认识形成难学并且不实用,不知学为何用的直观印象.
随着信息技术的飞速进步,以离散数据处理作为实际应用背景,线性代数知识体系是很多工程技术的基础,对于我校优势的信息科学学科群而言,线性代数课程是最重要的公共基础数学课程之一.在线性代数课程教学中建设有效的教学案例,让学生在学习抽象理论的过程中对于理论所涉及的背景和潜在应用具有更加深刻的认识,在抽象理论的教学和专业需求之间建立有效的契合,就可以充分调动学生的学习兴趣,培养学生的探索和创新思维,使得线性代数课程的教学更好的达成目标.
2 当前国内外在案例建设上的探索
国外线性代数课程的改革以美国作为代表,始于二十世纪九十年代,强调线性代数课程要面向应用,满足非数学专业需要,强调课程教学应面向矩阵且根据学生的水平和需要来组织,突出课程对于科学计算技术的应用.以在美国大学理工科各专业广泛使用的《线性代数及其应用》这一教材为例,书中包含了约50道各类应用性例题和近200道应用性习题,其中的应用背景涉及计算机科学、数学、物理学、生物学、经济学和统计学等各专业学科[1,2].
近年来,国内各高校也在线性代数教学案例建设上开展了广泛的探索[3,4],具体的形式有两类:一类是探索利用数学软件为平台并结合应用案例开展教学,相关案例教学过程中通过基本的数学原理,强调利用专业知识开展数学建模和利用科学计算软件进行应用计算[5,6];另一类是探索在理论知识教学的基础上建设专门的教学案例来加强理论应用环节,相关案例强调利用线性方程组进行数学建模的思想,在一定程度体现了科学计算软件的应用[7,8].
国内外的系列探索都显示了案例建设在线性代数课程教学改革中的突出地位,但是由于各个学校在专业需求、学生培养目标和教学背景上的差异,案例建设必须结合实际情况,有针对性、系统性的规划和开展,才能更好的服务于课程教学.
3 课程知识应用分析及案例建设的思考
我校具有优势的信息科学学科群,随着近年来信息技术的飞速发展,对于以线性代数为基础的数学知识及工具的应用需求日益突出,对于课程教学提出了新的要求,一个最直接的要求就是希望能够让学生打好数学理论基础的同时能够具备一定的应用能力,在充分调动学习的主观能动性的同时为进一步的专业学习打下理论基础、思维基础,建立起基础课教学和专业课教学的桥梁.
结合线性代数的基础理论和信息科学学科的专业需求背景,线性代数课程的理论基础在专业学习和应用中的表现主要体现在以下两个方面.
一是在思想层面上,“以直代曲”是处理很多复杂问题时很自然的思想,很多实际问题往往可以通过抽象和简化实现线性化,因此利用线性方程组进行建模并求解问题的思维方法是工程技术和国民经济许多领域一种有效工具;
二是在数学工具层面上,在数学、物理学和信息科学以及社会科学的很多研究与应用中,线性代数知识被很多方法和技术作为理论和算法基础的一部分,有着各种广泛而重要的实际应用;此外线性代数知识为很多后续课程提供了理论和算法基础,对不少专业而言是一门具有先导性作用的基础数学课程.
基于上述分析,系统建设线性代数课程教学案例必须综合考虑这两个层面的应用需求,建立不同体系的教学案例:
第一类体系的案例可以称为建模案例,主要体现思想层面的训练,着重训练针对实际问题进行数学抽象和建模的能力,特别是针对实际应用进行抽象和建立线性方程组的能力.这类案例在当前教学实践中得到了比较充分的挖掘,部分高校已经编写了案例汇编并应用于教学实践[9],其中比较具有代表性的案例包括:交通网络流量分析问题、投入产出问题、配方问题、人口流动问题、生物种群增长问题、平板温度测量问题等.
第二类体系的案例可以称为基本应用教学案例,主要体现线性代数课程的部分知识点作为基本数学工具在不同专业中的应用,尤其是作为课程核心知识的矩阵、向量和线性变换等知识在数学、物理学和信息科学等专业学科中的应用.目前建设的代表性案例包括:Hill密码问题、几何变换问题等.与教学和应用需求相比,这类案例的建设在当前存在明显不足,仍需进一步的挖掘和研究,成为下一步教学研究的重点之一.
4 典型的基本应用教学案例及分析
本节针对当前教学中应用效果较好的两个不同类型基本应用教学案例进行分析,讨论这类案例建设的目标、设计过程及教学效果.
4.1 基本应用教学案例——图像信息伪装
4.1.1 教学知识点及案例建设的教学目标
矩阵乘法是线性代数课程中矩阵的一种重要运算,其应用贯穿于课程后续的所有教学章节,其运算规则表面上比较简单,但是矩阵乘法在思想本质上体现的是变换的复合,并且这一本质在工程实践中得到了广泛的应用,如果只是进行理论概念的教学,很难让学生体会到这一本质.因此在教学实施中可以设计基本应用教学案例来让学生充分理解这一运算规则的本质,并且可以通过对实际需求的渐进分析及案例的深入研究,引入有关逆矩阵和矩阵方程的教学内容.
4.1.2 案例的专业背景
课程教学在矩阵概念部分已经介绍了数字图像的数据与矩阵之间具有一种天然的联系:灰度图像按照行列排列的每个像素点包含一个灰度数值,数值范围是0~255,因此灰度图像本质上就是一个矩阵,通过matlab可以读取出相应的图像信息,如图1所示.

图1 灰度图像的矩阵表示
由于本案例中使用彩色图像,尺寸为240像素*240像素,因此首先需引入图像的三原色理论:彩色图像的每一个像素点同时包含了红色(R)、绿色(G)、蓝色(B)三原色的信息,而每个单独颜色的信息与灰度图像一样,是一个0~255之间的数值,因此为了顺利引入矩阵表示形式,首先将数字图像数据分解为单独的红色数据、绿色数据和蓝色数据,每种颜色的数据就是一个矩阵(如图2所示),在案例的实际应用中,每次只对其中一种颜色的数据进行运算,最后再将变换所得的三原色数据合并成彩色图像.

图2 彩色图像的分解及矩阵表示
4.1.3 案例的教学应用
在完成矩阵乘法基本数学原理教学之后,引入该案例巩固对矩阵乘法的理解并深入分析面临的实际问题.
首先介绍案例的基本数学原理:矩阵乘法,即利用一个密钥矩阵B右乘原始数据的矩阵A得C=AB,将C中的数据作为原始数据的一种伪装信息,如图3所示.
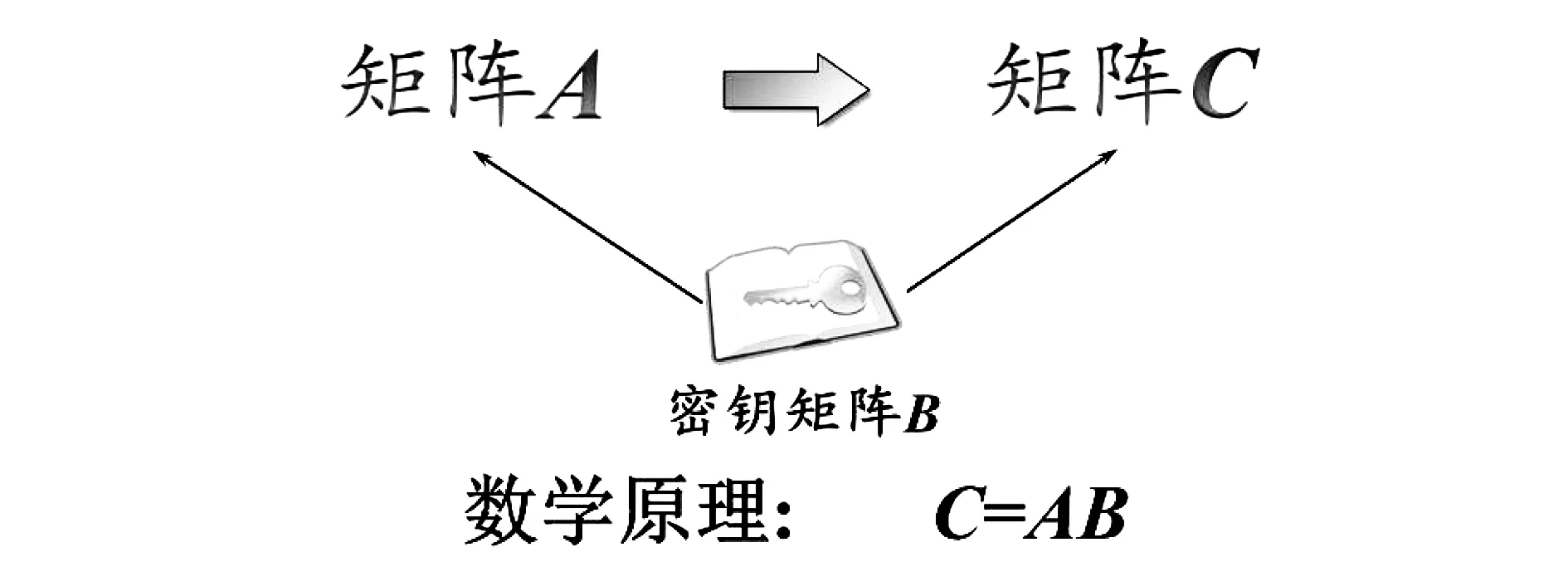
图3 信息伪装的数学原理—矩阵乘法
由于案例的背景直观,原理简单,因此在课堂教学中利用matlab2010开展实验,并输出实验结果,如图4所示.从实验结果可以看出,通过简单的矩阵乘法应用,就可以对实际图像中的重要信息进行有效的伪装.学生同时也可以直观认识到上述矩阵乘法的过程就是将密钥矩阵所包含的变换信息复合到图像矩阵这一本质.

图4 信息伪装的实验结果
4.1.4 案例的深入讨论
结合上述案例的实验结果,在教学中还可以进一步提出可以深入讨论的问题,第一个问题是实际应用中非常自然的一个想法:对于已经进行信息伪装的图像是否可以还原得到原始图像呢?这个需求对于伪装的密钥矩阵B是否有特殊要求?此外,可以进一步引导学生提出实际需求的另外一个自然想法:是否存在更好的信息伪装方式?例如:是否可以将一副图像伪装成另外一副图像呢(如图5所示)?上述需求抽象所得的数学问题是:若已知AX=C(或XA=C),A与C为已知方阵, 是否可求解X?这样就可以自然引出逆矩阵和矩阵方程等后续知识.在后续教学应用中,对该案例的拓展讨论在加深学生对逆矩阵理论认知的同时可以进一步让学生领会高阶矩阵求逆在实际应用中面临的系列问题,能够很好的达成教学目标.

图5 图像伪装实验示意图
4.2 基本应用教学案例——文本信息检索
4.2.1 教学知识点及案例建设的教学目标
向量和向量组是线性代数课程的重要概念之一,进一步而言,由向量组引出向量空间并进一步拓展为线性空间是最能体现线性代数课程及思维特点的精彩环节.当前教学主要从几何层面引入了向量、向量组等概念和教学内容,这种手段对于强化抽象概念的理解有重要促进作用,然而也存在一定的不足.例如:在几何层面只能形象描述不超过三维空间的对象,不能形象描述高维向量,这一不足恰好是学生在相关概念和内容学习时感到抽象的难点所在,并且这种几何形象不足以有效克服学生对线性空间这一抽象概念的理解.而在信息学科中,高维向量、线性变换等线性代数的概念和方法作为很多研究的基础手段得到了广泛应用.因此在相关内容的教学中结合大一学生的特点和信息学科的应用,引入了文本信息检索基本教学案例.通过这一日常生活中不可或缺的应用让学生充分理解高维向量和向量组的概念、基本运算,并且可以在后续教学中将背景拓展到图像检索、视频检索等领域,使线性空间这个抽象概念变得更加形象,也为线性变换这一抽象概念的形象理解和具体应用提供了基础.
4.2.2 案例的专业背景
“向量空间模型(VSM:Vector Space Model)”是20世纪70年代提出并得到成功应用的一个信息检索模型.该模型应用于文本信息检索时在向量组构建、相似度计算等过程中广泛应用了向量组和欧氏空间教学内容的系列相关知识,对于学生理解和应用线性代数课程的相关教学内容具有重要参考价值.由于信息检索在实际研究和应用中涉及了较多的专门领域知识,为简化模型和突出课程教学内容,基本教学案例在设计时以简单的文本信息检索为背景,只讲解以短句为背景的向量构建和相似度计算问题,引入了“中文分词”、“词频”和“词典”这三个形象易懂的专业领域概念,将案例的重点突出在向量和向量组的概念引入和相似度计算等线性代数知识的应用上.
中文分词:中文分词是将文章或语句中连续的汉字切分为单独且有含义的“词”.英文词语之间有空格作为天然分割符号,而中文词语之间没有分隔,因此将文本信息分割为基本表示单元的“词”成为文本信息向量化及深入分析的基础,基本原理如图6所示.
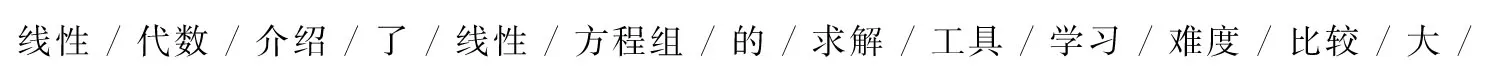
图6 中文分词示意图
词频:词频是指某个词语在文章或语句中出现的次数,可以作为词语重要性的一种度量手段.在实际应用中为排除介词、副词、助词等虚词干扰,一般只统计名词、动词、数词、形容词等实词,同时为处理不同长度文章在词频上的差异问题会采用归一化处理手段.教学案例因为只是简单衡量短句之间的相似程度,因此直接统计实词的词频即可,如图7所示.
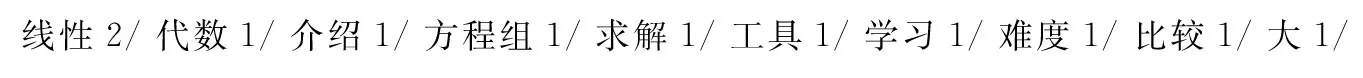
图7 词频统计示意图
词典:文本分析中的词典并不是传统用于词语解释的词典,而是为处理分词后文章词语及其数量不一致导致后期分析不能有效开展这一问题提出了一种解决方案:通常按照研究的实际问题,指定一定数量的词语建立词典,在完成分词后只统计词典中词语的词频来建立向量.例如:两个语句分别为“线性代数内容抽象学习难度比较大”和“线性方程组求解方法不唯一”,完成分词和词频统计的结果示意图如图8(a)所示,两个向量分别为8维和5维,并且词频数字对应的词语并不一致,无法进行后续分析.而选定“线性、代数、内容、抽象、学习、难度、大、方程组、求解、方法、不唯一”这11个词建立词典,那么两个语句在分词和完成词频统计后对应了两个同样为11维的向量,并且向量各维可以对应相同的词语,如图8(b)所示.

图8 词典用途示意图
通过分词和词频统计,可以有效的实现中文信息的向量化处理,这种方法不仅可以让学生直观理解了高维向量的概念,而且可以让学生掌握将现实对象抽象为数学概念的一种重要手段.而词典的引入则与教学内容中的向量组建立了直接的联系,使得这一抽象概念变得形象和直接.
4.2.3 案例的教学应用
在完成向量组与欧氏空间基本数学原理教学之后,引入该案例巩固对数学概念和部分运算的理解,并对案例应用进行拓展,分析面临的实际问题.
首先介绍案例的基本数学原理:向量的长度

及向量夹角余弦
以向量夹角余弦值作为文本相似程度的度量标准,其中值0表示完全不相同,值1表示完全相同.在课堂教学中选择三个短句,如:T1“线性代数课程内容抽象学习难度比较大”、T2“线性代数课程抽象但并不难学”和T3“线性方程组求解方法不唯一”.选择“线性、代数、课程、内容、抽象、学习、难度、大、不难学、方程组、求解、方法、不唯一”作为词典,通过词频统计将三个短句抽象为三个高维向量,分别为
T1=(1,1,1,1,1,1,1,1,0,0,0,0,0), T2=(1,1,1,0,1,0,0,0,1,0,0,0,0),
T3=(1,0,0,0,0,0,0,0,0,1,1,1,1),
将向量T1,T2夹角记为θ1,将向量T1,T3夹角记为θ2,将向量T2,T3夹角记为θ3,则向量夹角余弦值分别为cosθ1≈0.63,cosθ2≈0.16,cosθ3=0.2.从向量夹角的余弦值可以发现,语句T1和T2相似程度较高,而二者与T3的相似程度都不高,这与短句的书面含义相似程度基本一致.
4.2.4 案例的深入讨论
结合案例的实验结果,在教学中还可以进一步在两个不同方面进行深入讨论:第一个拓展的方向是如果文章数量很多而且长度比较长,在进行相似度计算时是否可以进一步提出更好的方法?对这个方面的拓展可以引导学生将向量组转化矩阵,并为后续的特征值与特征向量的学习埋下伏笔.第二个拓展的方向是将对象更换成分辨率相同的图像而不是文本,那么抽象所得的数学概念就会转变为同型矩阵,由同型矩阵构成的集合与向量组这样的集合在数学本质上具有什么样的联系和区别?学生在这方面的思考可以在后续教学中增强对线性空间等抽象概念的理解,帮助理解向量空间与线性空间的联系和区别,并且可以在后续学习中通过部分数字图像处理方法的介绍强化对线性变换这个抽象概念的理解与应用.
4.3 案例的特点和启示
上述两个不同类型的案例体现了一个共同的特点:专业知识背景简单易懂,对线性代数知识应用直接,并且实验结果能够有效吸引学生兴趣,方便在课堂教学中进行演示.案例很好的体现和演示了课程知识点的本质,并且对案例的深入分析可以进一步联系相关知识点的后续教学内容,既是对课程理论知识教学的一种强化和拓展,也可以很好的锻炼学生对实际应用问题的数学抽象和建模能力,同时也可以在应用问题和思考中锻炼学生的探索能力,启发学生发现理论知识在实际应用中存在的问题和解决问题的方法.通过案例在教学实践中的应用及取得的良好效果,为基本应用教学案例的进一步建设提供了有效的参考.
基本应用教学案例建设应该联系我校优势的信息科学专业学科,直观体现数学知识的力量,同时必须切实考虑学生的能力背景.综合而言,基本应用教学案例要做到“专业背景简单直观且体现专业学科的需求背景,数学原理应用直接,实施方案简洁直观,效果突出;在应用需求和数学理论需求方面应具有启发性,易于按照需求进行拓展和深入研讨”.
从上述特点和要求也可以发现,要系统建设好基本应用教学案例,在专业需求背景和数学理论基础的联系上具有较高的要求,因此其建设模式必须突破当前工作中完全依靠线性代数任课教师的模式,可考虑首先以课程知识点为基础,在学校各专业学科开展深入的调查和研讨,系统界定线性代数课程与各专业学科联系紧密的知识点和潜在的应用背景;然后在此基础上,协调线性代数课程教师和专业学科的教师,以前期界定的知识点和应有背景为基础,以强化线性代数课程知识点为目标,以建立基础理论和专业需求的联系桥梁为落脚点,系统建设和完善专业背景简单,数学原理直观,教学和实验效果突出的基本应用教学案例.
5 总结和展望
线性代数作为一门重要的公共基础数学课程,具有自身的突出特点.近年来随着信息技术的飞速发展,对线性代数课程的教学内容和教学目标提出了更高的要求,国内外高校在课程教学改革上做出了不少有益的探索,其中的一项重要措施就是开展线性代数课程教学案例建设,以突破课程内容抽象的这一特点给学习带来的约束.通过近年来的探索和实践,我们一方面建设了课程建模案例,以锻炼学生的数学思维,另一方面,我们针对课程各个章节的部分重要知识点以数字图像处理、信息检索、交通网络等为背景在基本应用教学案例建设上进行了有效的探索,在教学中突出了线性代数知识点作为数学工具的强大力量.随着教学改革的深入开展,要系统建设课程教学案例,仍然要根据实际需求开展进一步的探索和研究.
[1] 申国伦,薛有才.中美一些《线性代数》教材分析与思考[J].大学数学,2009,25(5):202-206.
[2] David C Lay.线性代数及其应用[M].3版.刘深泉,洪毅等,译.北京:机械工业出版社,2005.
[3] 李尚志.《线性代数》新教材精彩案例(之一)[J].大学数学,2011,27(4):1-7.
[4] 李尚志.《线性代数》新教材精彩案例(之二)[J].大学数学,2012,28(4):5-12.
[5] 陈怀琛.线性代数要与科学计算结成好伙伴[J].大学数学,2010,26(S1):28-34.
[6] 陈怀琛,龚杰民.线性代数实践及MATLAB入门[M].北京:电子工业出版社,2009.
[7] 陈伏兵.应用线性代数[M].北京:科学出版社,2011.
[8] 谢政.线性代数[M].北京:高等教育出版社[M].2012.
[9] 东南大学数学系.线性代数建模案例汇编[OL].2009; http:∥max.book118.com/html/2015/0904/24649856.shtm.
Research on Teaching Case Construction of Linear Algebra
WENJun,QuLong-jiang,YIDong-yun
(College of Science,National University of Defense Technology,Changsha 410073,China)
The exploration on teaching case is analyzed and summarized.Based on the deep analysis of curriculum knowledge application, practice of teaching case construction is systematic summarized and considered.Through analyzing a typical case, the paper researched on the preparation of further work.
linear algebra; case construction; application; analysis; consideration
2016-04-05; [修改日期] 2016-07-28
文军(1976-),男,博士,副教授,从事多媒体信息系统及数据处理研究.Email:axing1978@sina.com
G642
C
1672-1454(2016)06-0046-07

