太阳影子定位技术研究

张 露，杨鹏辉，张德鑫，阚 剑

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

太阳影子定位技术研究

张 露，杨鹏辉，张德鑫，阚 剑

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目的 针对太阳影子定位问题，建立一系列数学模型对视频中的数据进行研究，并通过太阳影子定位技术确定视频拍摄时间与地点。方法 以一段时长30 min拍摄时间与地点未知的直杆影长变化视频为研究对象，根据全国大学生数学建模网提供的数据，运用最小二乘拟合、构建方程组求解、画图分析以及图片灰度处理、锐化处理等方法，分别构建了影长变化模型、影子定位模型和影子定时模型等，并依据影子的坐标点，结合MATLAB、Excel等软件得出了影子长度的变化规律、目标物所在地的经纬度以及测量数据的时间。结果 经画图分析得知2015年10月22日北京时间9∶00～15∶00之间天安门广场(北纬39度54分26秒,东经116度23分29秒)3 m高直杆的太阳影子先随时间的推移而变短，在中午某一时刻达到最小值，后又随时间的变化而变长；在只知直杆在水平地面上的太阳影子顶点坐标的情况下，求得实例中直杆所在地点为(37.707 23 °N,71.788 99 °E)，测量日期为11月10号；在只获取一段视频的情况下，经过对图片截取、灰度化以及锐化等处理读取出视频中直杆影子顶端坐标，并求得该视频的拍摄地点与时间分别为(40.16 °N,122.70 °E)、2015年7月26日。结论 在视频中物体所投射的影子坐标可读取的情况下，运用合理的数学模型，可以通过太阳影子的变化对视频的拍摄时间及其地点进行精准的判断。

最小二乘拟合法；太阳高度角；MATLAB；Excel

在古代，人们就利用太阳投射的影子来测定时刻，并发明了闻名世界的计时仪器“日晷”。汉书天文志有“夏至至于东井，北近极，故晷短；立八尺之表，而晷景长尺五寸八分。冬至至于牵牛，远极，故晷长；立八尺之表，而晷景长丈三尺一寸四分。春秋分日至娄、角，去极中，而晷中；立八尺之表，而晷景长七尺三寸六分。”可见古人对利用太阳影子进行定位进行过一定的研究。在现代，如何确定视频的拍摄地点和拍摄日期则成为视频数据分析的重要方面，而太阳影子定位技术就是通过分析物体的太阳影子变化，确定视频拍摄地点和日期的一种重要方法。众所周知，视频数据的分析在现代生活中具有重要的意义，特别是对于刑事案件的侦查起着突破性的作用。国内外学者基于日晷原理，结合现代数学软件探索太阳影子定位技术。但这项技术还不够成熟，有待学者们继续深入研究，以便将其应用于现代通信与监测等领域。基于这样的研究背景，运用赤纬角算法和时差算法等现代数学知识对太阳影子定位技术做了一定深度的研究。

1 数据来源与模型假设

数据主要来源于全国大学生数学建模比赛。为保证文章的严密性，现做出以下几条假设：(1)设地球大气层对太阳高度角没有影响，即忽略大气层对实际观测的太阳高度角和理论值的不同影响;(2)设太阳、地球都是一个表面光滑的正球体；(3)太阳光为一束平行的光束；(4)目标地直杆与水平地面呈垂直状态；(5)时差算法以北京时间为准。

2 影子长度的变化规律

2.1 研究思路

建立影子长度变化的数学模型，并且分析影子长度关于各个参数的变化规律。在忽略大气对光线折射的因素下，易知影子的长度与目标所在地的经度、纬度、太阳高度角等因素存在某种相关性。于是首先尝试建立影子长度与经纬度、太阳高度角等各因素之间的关系，分析影子长度关于各个参数的变化规律；然后基于各因素之间的变化规律，利用抽象几何的画图研究方法，推导出太阳高度角与当地经纬度、太阳赤纬角及时角之间的函数变化关系，从而推导出太阳赤纬角以及时角的计算公式；最后利用时差算法及赤纬角算法对模型进行修正并推导出影长变化公式，带入实例数据，运用MATLAB编程画出实例中直杆的太阳影子长度的变化曲线，求其变化范围。

2.2 研究方法

2.2.1 模型的建立

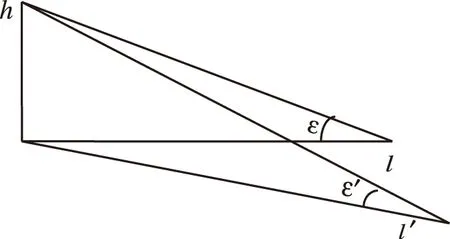
图1 影长模型图

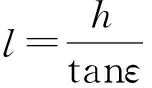
若需求得直杆影长，需先求得角ε。又易知ε为太阳高度角，太阳高度角由目标所在地的地理纬度γ、当日的太阳赤纬ω以及当时的太阳时角τ等因素共同决定[1]。各角度几何图示如图2。

已知各个角度之间的关系满足如下公式：

sinε=sinγsinω+cosγcosωcosτ

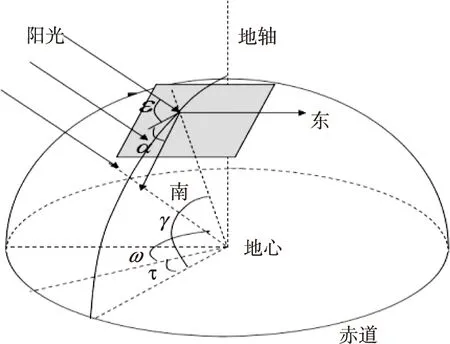
图2 几何角度图

其中太阳赤纬ω是由观测当日日期在1年中的序号n所决定：

sinω=0.39795cos[0.98563(n-173)]

太阳时角τ则是由真太阳时T所决定：

τ=15×(T-12)

而真太阳时又是由北京时间T′及观测地时差m两者共同决定：

T=T′-m

这其中时差又是随经度φ变化的函数：

m=(120 °-φ)/15 °

建立以上关系式可以得出太阳高度角关于目标所在地的地理纬度γ、观测当日日期在1年中的序号n、观测点的北京时间T′以及观测点经度φ的变化关系式如下[2]：

其中

sinω=0.39795cos[0.98563(n-173)],m=(120°-φ)/15°

综上可知，求1根直杆的影子长度，需了解该直杆长度h、所在地地理纬度γ、观测当日日期在一年中的序号n、观测点的北京时间以及观测点经度φ。

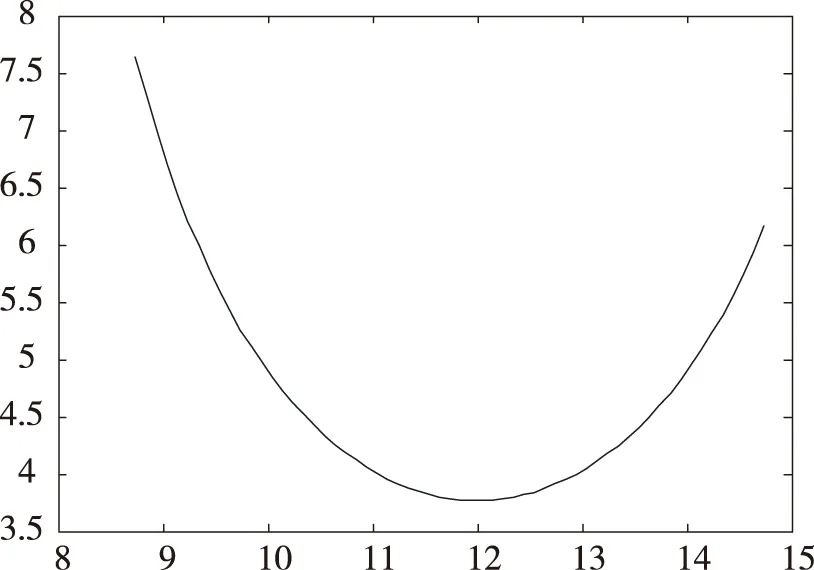
图3 直杆影子长度变化曲线图

2.2.2 模型的求解

已知2015年10月22日北京时间9∶00～15∶00之间天安门广场(北纬39度54分26秒,东经116度23分29秒)有3 m高的直杆，即有h=3，γ=116.3914，n=295，φ=39.9072，T′=t(t∈[9,13])。将上述数据代入所求公式,运用MATLAB画图可得出该时间段观测点直杆影子长度变化曲线如图3。

观察图3中曲线可知，该时间段内影子长度先随时间的推移而变短，在中午某一时刻达到最小值，后又随时间的推移而变长，整个时间段影长变化范围为3.56～7.67 m。

3 基于影子变化的定位技术

3.1 研究思路

根据某固定直杆在水平地面上的太阳影子的变化，建立数学模型,确定直杆所处的地点。首先要获取影子的顶点坐标。对于在水平地面影子顶点坐标的获取，是以直杆底端为原点、水平地面为xy平面建立的坐标系，虽然坐标轴方向的选取影响了影子的坐标，但是对于1天内影子顶点的运动轨迹以及影长的变化规律不会产生影响，并且影长的最短处对应的当地时间应为正午12点。以时间变化为横坐标，影长变化为纵坐标建立直角坐标系，在坐标系内运用影子定点坐标拟合出影长的变化曲线图，求出影长的最低点；再根据测量时的背景时间以及测量的间隔时间，推算出测量地的正午12点和北京时间的时间差，从而根据时差和经度的关系推算出测量地的经度。由于直杆长度与位置无关，所以可以通过与太阳高度角的比值忽略掉直杆长度的影响，进而就可代入数据求出直杆所在的纬度，确定测量点的位置。

3.2 研究方法

3.2.1 对经度的求解

I 数据处理

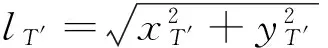
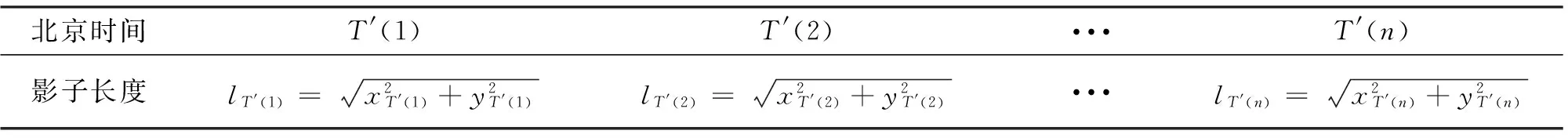
表1 不同时刻影子长度对应表

II 最小二乘拟合

以时间(T)为横坐标，影子长度(L)为纵坐标建立影子长度与时间变化的坐标系，在建立这个坐标系之前，需要对横坐标即时间变化做一定的处理，把时间的分钟数同除以60换算成小时制，然后结合影子长度建立影子长度变化的坐标系。在坐标系内将测量所得的数据运用MATLAB进行拟合，得出时间与影长的函数y=ax2+bx+c(a≠0，并且利用最小二乘法判断其拟合是否合理。

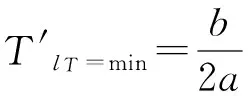
3.2.2 对纬度的求解

在上述太阳高度角、纬度、日期和太阳赤纬的关系中，已知日期、太阳赤纬是与真太阳时(当地时间)构成某种函数关系。若以当地时间作为自变量，则只有太阳高度角和纬度是需要求解的。当建立太阳方位角公式时，太阳方位角就可以通过影子顶点的纵坐标与影长的比值解出，所得结果即为太阳高度角与纬度之间的关系。

已知太阳方位角公式为：

建立公式sinε=sinγsinω+cosγcosωcosτ，化简可得到如下方程：

代入数值即可求出当地纬度γ[4]。

4 基于影子变化的定时技术

4.1 研究思路

根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型，确定直杆所处的地点和日期。首先根据太阳高度角和太阳方位角的公式，推导出日期和纬度的联合公式，将所测得的影子坐标进行处理，得出太阳方位角的余弦值，再将不同的影子长度和时间所对应的坐标带入方程，运用MATLAB程序得出纬度值和日期，从而得出可能的测量地点和日期。

4.2 研究方法

4.2.1 对时间的求解

在地球自转和公转的过程中，某一地点的正午太阳高度角既和所在地的纬度有关，又与测量的日期以及在该日期测量的时间有关。同一纬度不同日期的正午太阳高度角不同，同一日期不同纬度的正午太阳高度角也不同，因此在给定影长时，测量地的位置以及测量的日期都是可以确定的。

在如下公式中：

sinε=sinγsinω+cosγcosωcosτ

对太阳高度角求其反函数，即可得出太阳高度角ε的表达式为：

ε=arcsin(sinγsinω+cosγcosωcosτ)

由图1可看出，太阳高度角ε也可表示为：

因此同一地点不同时刻的太阳高度角的比值方程为：

此时，同一地点不同时刻的太阳高度角ε正切值的比值与影长相关，与直杆的高度无关。

将ε的表达式带入太阳高度角的比值方程，即可得出纬度日期模型：[5]

模型中的纬度、测量日期、太阳赤纬共同决定了测量地的太阳高度角的数值，将实际测量的影子长度和时间数据带入模型，运用MATLAB程序可解出测量地的纬度和测量日期。

4.2.2 举例说明

有一直竿垂直于地面，以直竿底端为原点、水平地面为xy平面建立坐标系，其影子坐标变化如下表2：

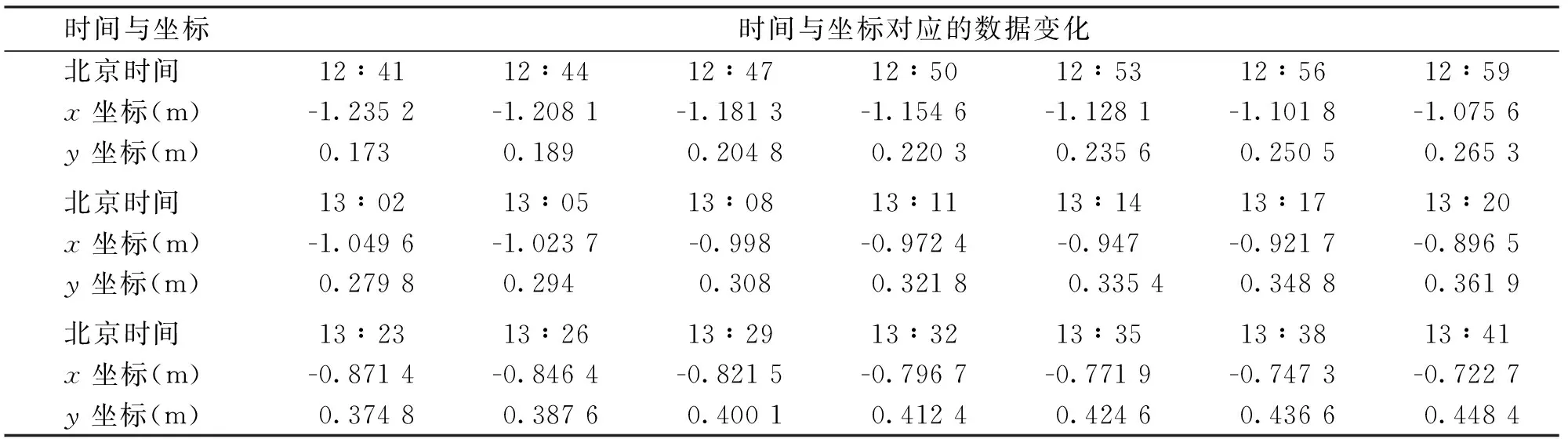
表2 影子坐标变化表

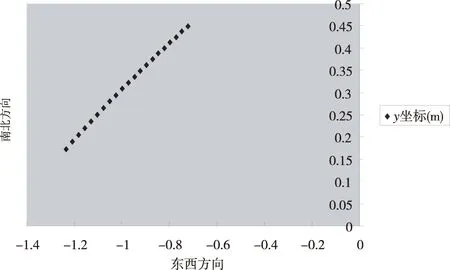
图4 影子落点坐标图

以直杆底端为原点，东西方向为横轴，南北方向为纵轴，建立影子落点的坐标系，将上表中的数据在坐标系中画出，如图4所示：

根据影子落点坐标图，对应表2中测量每个点的北京时间，首先对北京时间进行处理，把时间的分钟数换算成小时制，如表3。

表3 处理时间表

表4 不同时刻影子长度对应表

将不同时刻影子长度对应表中的数据，运用MATLAB程序进行曲线拟合，拟合曲线如图5所示：

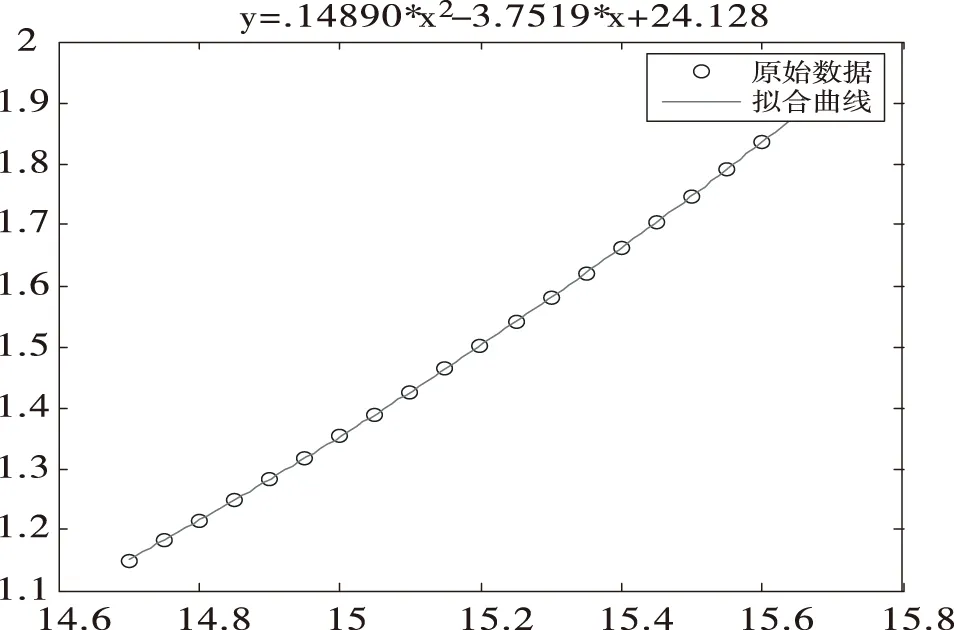
图5 影子长度变化图

得出影子长度和时间的二次方程：

L=0.09812T2-2.985T=23.319

误差的平方和为4.402588e-0.07，由于误差和极小于1，故此函数拟合程度较高。

在此方程中，影长l的最低点对应的时间即为测量地的正午12点所对应的北京时间：

此时测量地与北京时间的时差为：

则当测量地时间为正午12点时，对应的北京时间为15.214 07，由于Δt>0，故测量地在北京时间所在时区的经度120 °E的西边，由于地理上经度相隔1 °时，时差为4min，故测量地经度由公式：

可求得：

φ=71.78899°E

因此测量地所在的经度为71.78899 °。

由表2数据中，选取前2个点对应的影长和当地时间，带入纬度日期模型，因为：

τ=15×(T-12)

借助MATLAB程序，运行后结果为：

x=37.7072，y=162.5577

x即所求纬度，y是太阳赤纬。

由公式：

sinω=0.39795cos[0.98563(n-173)]

可反推出测量日期在1年中的序号n的表达式为：

将程序运行出的y(即ω)值带入反推出的公式，计算出n≈314，即11月10日。

结合经度模型和纬度日期模型，案例中数据求解结果为：该地点地理位置约为：37.70723 °N,71.78899 °E，测量日期为11月10日。

5 基于影长变化对视频拍摄时间地点的判断

5.1 研究思路

在上述问题中已经解决了在目标物影子坐标已知的情况下，根据太阳影子求目标物所在地及拍摄时间等问题。下面探讨如何根据太阳影子直接从一段视频中读取其拍摄时间及地点等信息。利用太阳影子定位技术，首先要从视频中读取影子的信息，即影子随时间变化其坐标点的变化。然后利用太阳高度角和太阳方位角的公式，推导出日期和纬度的联合公式，将所测得的影子坐标进行处理，得出太阳方位角的余弦值，再将不同影子长度和时间所对应的坐标带入方程，运用MATLAB程序得出纬度值和日期，从而得出可能的测量地点和日期。在此问题中对影子坐标的读取最为关键[6]。

5.2 研究方法

5.2.1 视频数据的读取方法

首先要将视频数据转换成图片数据，即等时间段对视频进行截图处理，但凭主观感觉进行截取误差太大，故需要运用MATLAB对视频数据进行读取处理。由于视频是由一帧一帧的图片组合而成，所以要想读取视频中的图片数据需先弄清楚这段视频由多少帧图片组合而成。

把所需读取的视频导入MATLAB中，读取视频信息如图6。

图6 视频读取信息

从视频信息中可知该视频时长为2 440s，该视频的帧率为25Hz，即每秒25帧图片，所以该视频总共有61 000帧。若每两分钟截取一张图片，总共可得21张图片。[7]

5.2.2 影子顶点坐标的读取方法

1张图片是由无数个像素点组成，可以利用MATLAB读取各像素点坐标，从而推导出直杆影子顶点坐标，为降低计算量，先对图片进行一定的处理。根据主观判断选取直杆底部一点读取该像素点坐标为(866,882)，然后再读取21张图片影子顶点的像素点坐标，发现其变化范围为x∈(867,1 700),y∈(780,930)，故截取图片影子所在的一部分进行灰度处理，截取图片如图7。

图7 影子截图

图8 灰度处理效果图

为了使影子图像更加清晰，需要利用图像锐化技术，使直杆影子的边缘变得清晰，从而使得影子顶点坐标的读取更加精准。图像锐化处理的目的是使图像的边缘、轮廓线以及图像的细节变的更加清晰，但平滑的图像变得模糊的根本原因是图像受到了平均或积分运算的影响，因此需要对其进行逆运算，使图像变得更为清晰[9]。利用Photo-Shop的图像锐化处理，锐化处理效果如图9所示。

图9 锐化处理效果图

经过上述处理，影子顶点已经变得清晰可见，只需读取出影子顶点坐标即可。但读取出的坐标仅为像素坐标，还需把其转化为实际的坐标才能进行影子定位技术运算。实际坐标可由摄像机坐标系与图像坐标系共同推导得出。设在图像坐标系中，以图片中直杆底端为原点，以毫米为单位的影子顶点坐标为(α,β)，以像素为单位的影子顶点坐标为(x,y)，且影子顶点像素点在x与y轴方向的物理尺寸为Δx,Δy；在摄像机坐标系中，以摄像机为坐标原点的影子顶点坐标为(φ,φ,γ)，且焦距f近似为摄像机与图像坐标系原点之间的直线距离；在实物坐标系中，以实际的直杆底端为坐标原点，影子顶点坐标为(x,y,z)，则三个坐标系下的影子顶点坐标之间的转化关系为：

(x,y,z,1)T=w(φ,φ,γ,1)T(w为4×4阶的矩阵，是对摄影机坐标系下的坐标进行旋转变换所得)

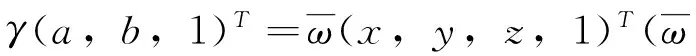
运用MATLAB进行上述坐标变换，最终得到影子顶点坐标，如表5所列。

表5 影子顶点坐标

根据上面叙述的方法，用影子顶点坐标求得该视频的拍摄地点与时间为(40.16 °N,122.70 °E)、2015年7月26日。

6 讨论与结论

物体的影长受到物体自身的体积、物体所在地的经度和纬度、观测日期及时间点等因素的影响。要通过物体影子的长度及影子坐标来确定物体的经纬度，需要根据观测日期、太阳高度角以及方位角的公式来建立模型，确定物体的位置；在失去观测日期等条件时，进一步优化模型，只需利用目标物影子顶点坐标变化也可求出拍摄时间与地点；而当影子顶点坐标这一唯一条件也失去时，可以利用图片截取、图片灰度处理、图片锐化处理以及坐标系转换等方法重现影子顶点坐标，从而求取视频的拍摄时间与地点。经过上述分析与讨论可知在只获取一段视频，而其他任何条件未知的情况下，通过一系列的图片处理与数学演算，求取视频的拍摄时间与地点是可行的。

[1]刘伟峰,谢永杰,陈若望,等.天顶亮度与太阳高度角关系的观测[J].光电工程,2012,(07):49-54.

[2]栗琳,胡勇,巩彩兰,等.太阳高度角对图像能量的影响及其校正[J].大气与环境光学学报,2013,(01):11-17.

[3]王国安,米鸿涛,邓天宏,等.太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学,2007,(01):161-164.

[4]李先华,黄雪樵,池天河,等.卫片像元太阳高度角和方位角的计算原理与方法[J].测绘学报,1993,(02):149-154.

[5]杨长青,李华,徐宝芳.“正午太阳高度角模型”的设计、制作与运用[J].中学地理教学参考,2011,(08):26-28.

[6]杨桂元.数学建模方法[M].合肥：中国科学技术出版社，2014：1-58.

[7]任利平.视频中关键帧提取技术的研究[D].兰州：兰州大学,2011.

[8]李贞培,李平,郭新宇,等.三种基于GDI+的图像灰度化实现方法[J].计算机技术与发展,2009,19(07):73-75+79.

[9]靳佳澍.一种针对彩色二维码图像的二值化方法[J].科技与企业,2016,(04):83-84.

[10]潘国荣,周跃寅.两种坐标系转换计算方法的比较[J].大地测量与地球动力学,2011,(03):58-62.

[责任编辑：刘守义 英文编辑：刘彦哲]

Sun Shadow Positioning Technology

ZHANG Lu,YANG Peng-hui,ZHANG De-xin,KAN Jian

(School of Statistics and Applied Math，Anhui University of Finance and Economics,Bengbu,Anhui 233030,China)

Objective The paper,according to the sun shadow positioning issue,establishes a series of mathematical models to study the data of the video,and determines the shooting time and site of the video through the sun shadow positioning technology.Methods Taking the video of 30-minute-long and unknown shooting site reflecting the length variation of the straight rod’s shadow as the research object,this paper respectively constructed the shadow’s length variation model,the shadow positioning model,the shadow timing model and other models by applying the least square fitting,the equation set,the graph drawing analysis,and the image processing of the gray scale and sharpening,based on the data provided by the contemporary undergraduate mathematical website in modeling.The paper also concluded the law of the shadow’s length variation,the longitude and latitude of the site in the object,and the time of the data measurement by MATLAB,Excel and other software,based on the coordinates of the shadow.Results Through the graph drawing analysis,it was found that on October 22,2015,Beijing time between 9∶00-15∶00,the sun shadow of the 3-meter-high straight rod firstly got short with time passing by,reached the minimum in a certain moment of the noon,and got long as the time varied.Under the circumstance that only the coordinate of the shadow’s vertex on the rod horizontal ground was known,it was calculated that in instance 1,the site of the straight rod was in the coordinate and the date of the measurement was November 10th.Under the circumstance there was only one piece of the video,the coordinate of the shadow’s vertex of the straight rod,the shooting site ofand the shooting date of October 22,2015.Conclusion In the case that the coordinate of the shadow projected by the object can be read;the shooting time and site of the video can be judged concisely through analyzing the changes of the sun shadow by applying the reasonable mathematical models.

least square fitting;solar elevation angle;MATLAB;Excel

国家自然科学基金项目(11301001)；安徽财经大学教研项目(acjyzd201429)

张露(1995-)，女，安徽六安人，安徽财经大学统计与应用数学学院在读学生，研究方向：数学与应用数学。

杨鹏辉(1981-)，女，安徽淮南人，安徽财经大学统计与应用数学学院讲师，硕士，研究方向：应用数学与数学建模。

O 242

A

10.3969/j.issn.1673-1492.2016.11.007

来稿日期：2016-04-18