改进粒子群算法优化的支持向量机及其应用

王振武，孙佳骏，尹成峰

（中国矿业大学机电与信息工程学院，北京100083）

改进粒子群算法优化的支持向量机及其应用

王振武，孙佳骏，尹成峰

（中国矿业大学机电与信息工程学院，北京100083）

传统粒子群优化（particle swarm optimization，PSO）算法主要包含两方面问题，即易陷入局部极小和后期震荡严重，为此引入混沌序列来初始化粒子群的位置，并在简化的粒子群数学模型上从两个方面对其进行了改进。本文利用改进的PSO算法对支持向量机（support vector machine，SVM）的参数进行优化，仿真实验结果表明：与SVM、PSO-SVM以及遗传算法（genetic algorithm，GA）优化的SVM（GA-SVM）相比，改进PSO优化的SVM（IPSOSVM）算法具有较高的分类准确率，并且与PSO-SVM算法相比，准确率提高了3％～5％，与PSO-SVM算法以及GASVM算法相比，IPSO-SVM的训练和泛化速度都明显提高。本文将IPSO-SVM算法应用到遥感影像的分类中，分类结果表明，与PSO-SVM算法相比，IPSO-SVM算法具有更好的分类结果。

粒子群优化算法；混沌序列；支持向量机；遥感影像

支持向量机（support vector machine，SVM）是应用最广泛的分类算法之一，该方法的核心思想是在特征空间寻找最优超平面将两类样本无误地分开，且分类间隔最大。该方法能够平衡模型的复杂性和学习能力，较好地避免了“过学习”和“维数灾难”等问题，保证得到的极值解是全局最优解，这也决定了该算法具有较好的泛化能力，近年来被广泛应用于遥感图像的分类中并取得了良好的效果。在SVM的应用中，模型参数选择的恰当与否会对遥感图像的分类效果带来较大影响。传统的SVM采用网格搜索交叉验证方法优化其参数，但此方法主观因素影响较大，同时搜索和验证过程耗时较长，且浪费相当数量的训练样本用于验证，在训练样本有限的情况下，其缺陷体现得更加明显。基于此，国内外学者开始将智能优化算法引入到SVM的参数优化中，其中最为广泛的是遗传算法（genetic algorithm，GA）和粒子群优化（particle swarm optimization，PSO）算法。遗传算法虽然具有较强的鲁棒性，但对所求问题的目标函数敏感性不高，且收敛速度慢，算法实时性差，而PSO算法具有导向性强、收敛速度快以及求解精度高［1］的特点，本文采用PSO算法优化SVM。

1 PSO算法和SVM原理简介

1．1 PSO算法原理及研究现状

PSO算法将优化问题的候选解抽象为一群无质量、零体积的粒子，这些粒子在d维空间中依靠自身的经验和群体中适应度最高的粒子的经验来不断的优化自身的位置。设一个由n个粒子构成的粒子群，其中第i个粒子在d维空间中的速度记为把位置记作可以将xi代入相应公式计算其适应度值并据此评价粒子i位置的优劣。粒子i的当前个体最优位置记为pbestid，整个粒子群的当前最优位置记为gbestd，粒子i通过式（1）来迭代更新自身的速度与位置。

国内外众多学者都对PSO算法的改进展开了研究。有些学者对式（1）中的惯性权重w进行了研究。文献［2］在迭代过程中线性递减w的值，因为适当增大w的值可以使算法在迭代初期具有较强的全局搜索能力，尽可能保证搜索到整个解空间，而适当缩小w的值能够保证群体后期趋向于进行局部搜索，即在有可能产生最优解的区域进行精细寻优，最终收敛到最优位置。但是由于PSO算法的寻优过程本身是非线性的，所以如果想要真实的反映算法的搜索过程，采取w线性递减的方案显然是不合理的，因此文献［3］采用模糊规则来动态调整w。文献［4］对w应该取某一固定常数还是随时间线性减小的问题进行了分析研究，讨论了两种方案对算法性能的影响并提出w的设置原则。有些学者改进了式（1）中的学习因子c1和c2，它们分别代表每个粒子趋向pbestid和gbestd的加速系数，反映了粒子的“个体认知”能力和群体的“社会引导”能力。文献［5］使c1和c2以时间为自变量线性递减，得出了为得到更好的效果需要根据特定的问题选取特定加速系数的结论，但很遗憾的是没有总结出普遍适用的规律，文献［6］提出了异步时变的加速系数，即在粒子寻优过程中以时间为变量，c1和c2分别进行相应的不同改变，但取得的优化效果并不理想，文献［7］在改进PSO算法的时变加速度系数的同时，也将其应用到综合减摇控制系统解耦控制器的设计中。有些文献对粒子群的拓扑结构进行改进，如文献［8］指出粒子群的拓扑结构会影响其搜索性能，对于简单问题应采用大规模的拓扑结构进行解决，而小规模的拓扑结构适用于求解复杂问题。文献［9］采用了多种连接方式不同的拓扑结构对PSO算法进行实验，得出了一般性结论，即任何一种PSO拓扑结构都不能适用于所有的基准函数，具体问题要具体分析。这是因为虽然连接方式不同，但这些拓扑结构都是固定不变的，因此文献［10］提出了一种动态的拓扑结构解决方案。另一些学者将PSO算法与其他算法结合使用。文献［11］提出了一种协同粒子群算法，它根据粒子的维数将粒子分为d个部分，然后对每一部分（d维中的其中一维）分别进行优化，通过计算适应度来评价每一部分的每一步搜索到的位置优劣，最后选取每一部分中历史的最优位置组成一个完整的粒子。文献［12］将PSO与GA的自然选择机制相结合，当算法更新完所有的粒子后，计算种群中所有粒子的适应度并进行优劣排序，然后根据结果，将适应度最差的一半粒子用适应度最好的一半粒子替换，但保留原粒子的个体历史最优位置信息。而文献［13］则将GA的其他两种机制借鉴到PSO中，即交叉机制和高斯变异机制，并在此基础上引入了模拟退火算法，以便更好的优化粒子群体。

在上述对PSO算法的改进中，大多数文献只针对PSO易陷入局部极小的问题提出了改进方案，并没有考虑PSO后期震荡严重的缺陷；在改进易陷入局部极小的缺点时，有的文献只是单纯的进行参数的修改，并不是从PSO算法收敛于局部极小的根本原因上采取改进策略；有的文献引入了一些新的参数或者将一些新的算法与传统的PSO相结合，虽在一定程度上得到了较好的寻优效果，但增加了复杂度，对收敛速度产生了较大影响。本文提出的对PSO算法进行改进的方案，不但提高了算法收敛速度，又同时解决了算法易陷入局部极小和后期震荡严重的缺陷，并将其用于优化支持向量机的模型参数以便更好的对遥感图像进行分类。

1．2 SVM算法原理

SVM的基本原理是建立一个最优超平面使得正负两类被正确地分开，并且保证分类间隔的最大化。1）线性可分情况:在原空间中求得能准确将正负样本完全分离的最优分类超平面；2）线性不可分情况:引入松弛变量ξi和惩罚参数C，容许错分样本的存在，并在最大分类间隔与最小分类误差之间寻求平衡。超平面的约束调节变为

广义的最优分类面变为

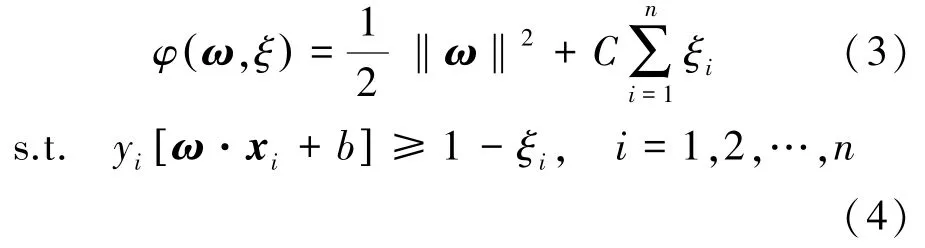
相应的分类决策函数表示为

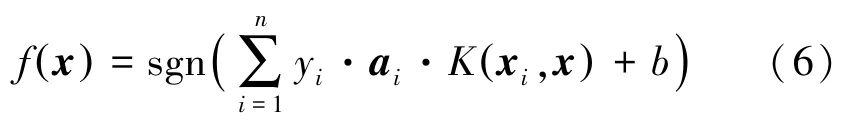
式中:ai为支持向量，b是分类的阈值。研究表明，C调节经验风险和VC维的平衡，可通过减少误差以实现对样本的较好分类，σ的大小决定着SVM是否对输入量的变化敏感，σ值过大会使SVM对输入反应迟钝，过小则会使SVM对输入过于敏感，所以要想对样本进行准确的分类就必须对参数进行优化，本文采用改进的PSO算法对SVM的上述参数进行优化。

2 IPSO算法原理

传统的粒子群优化算法其粒子群的初始位置是随机分布的。但是粒子群的初始位置会在一定程度上影响后续的寻优效果。因此本文利用混沌搜索的随机性和遍历性初始化粒子群使其能够均匀的分布于整个解空间，从而加快粒子群算法的收敛速度，有利于更快的得到全局最优解。

设问题解的维数为d维，利用混沌序列初始化粒子群初始位置的具体操作是:先产生一个d维、每个分量数值在（0，1）的随机向量然后根据Logistic方程对z1进行迭代，代到N个随机向量z1，z2，…，zN，将z1的各个分量按照式（7）映射到问题解的取值范围:

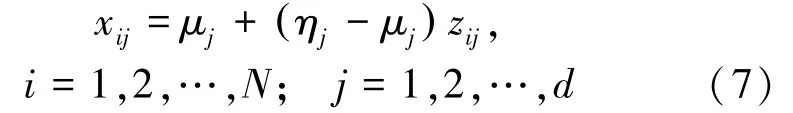
文献［15］中的定理1证明PSO算法可以不考虑粒子的速度，因为粒子的速度并不能反映出一个粒子趋近于最优位置的能力，反而可能会引导粒子向错误的方向进行搜索，影响了粒子的收敛速度与精度，据此本文对式（1）进行简化，简化后的粒子群优化公式为

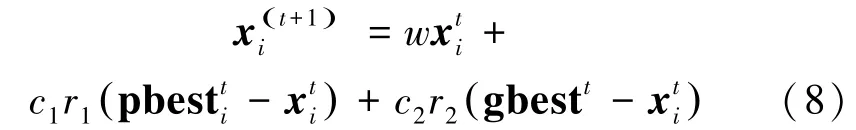
本文采用式（8）作为PSO算法的基础数学模型，剔除速度项简化了公式，从而减少了计算量，提高了搜索效率。传统PSO算法主要存在两点不足: 1）由于算法收敛速度快，粒子寻优存在趋同性，导致算法极易陷入局部极小；2）算法在寻优后期出现严重的震荡现象，从而对算法后期的收敛速度产生较大影响。

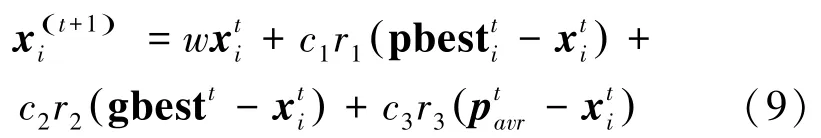
式（9）中引入新的学习因子c3和随机数是从所有个体粒子中选出的适应度优于且劣于所有其余粒子个体位置的平均值。在粒子的寻优过程中和三者共同向种群中的每个粒子传递信息，使每个粒子能获得更多的信息。由于的权值c3r3很小，相当于在式（8）的基础上增加一个小的扰动项以提高粒子的多样性，从而避免PSO的“过早熟”现象。对于问题（2），本文引入动量项来解决。令:

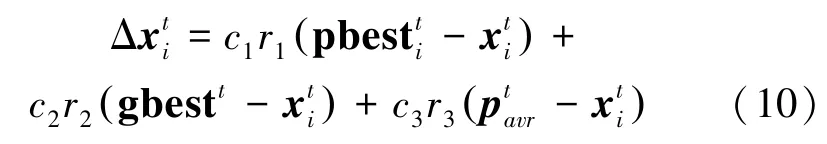
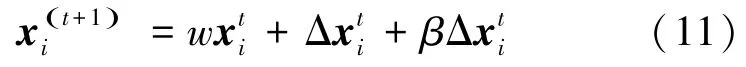
3 IPSO-SVM原理及实验结果分析

本文采用IPSO算法优化SVM分类模型中的两个参数，即式（3）中的参数C和式（5）中的参数σ，此SVM方法简记为IPSO-SVM，分类实验的算法步骤如下。

Input:已标记样本、测试样本。

Output:C和σ2、分类结果。

1）为PSO各个参数c1、c2、c3、w和β分别赋一个实数值，设置误差阈值和最大迭代次数itermax；

5）根据式（11）更新粒子的位置信息，利用适应度函数计算其适应度，更新个体的最优和全局最优gbestt；

6）检查结束条件，若满足则结束寻优，返回最优的参数组合(C，σ2)；否则转至4）。结束条件为寻优次数达到itermax或适应度值大于给定阈值；

7）利用最优的参数组合(C，σ2)建立的SVM分类模型进行分类。

为了验证IPSO-SVM算法的分类效果，选择流行的UCI（University of California Irvine）数据库中的4种数据集Wine、Iris、Ionosphere、Yeast进行算法验证，其中Yeast数据集选用MIT、NUC、CYT三类数据进行实验。对应的详细数据信息表格如表1所示。实验硬件和软件环境信息如下:CPU为Intel（R）Xeon（R）E3-1226 v3 3．30 GHz，内存为RAM 4．00GB，操作系统为Windows 7 64位，实验平台为VS．NET 2012，开发语言为C#。

表1 实验数据信息Table 1 Experiment data information

用表1所示训练样本和测试样本验证SVM、GA-SVM、PSO-SVM和IPSO-SVM 4种算法，得到相应的训练时间和泛化时间如图1和图2所示。GA-SVM、PSO-SVM和IPSO-SVM算法的最大迭代次数均为50次，粒子群或种群的数量均为40，遗传算法的交叉率0．8，变异率0．2，SVM算法采用径向基核函数，误差阈值10-3。如图所示，GA和PSO对支持向量机的优化（GA-SVM和PSOSVM算法）会减慢其训练速度，而IPSO-SVM则有效地加快了训练速度，同时，也一定程度上加快了泛化速度。理论上的原因在于，相比于传统的PSO优化算法，IPSO算法去除了粒子速度的概念，避免了人为确定参数对粒子训练的收敛速度的影响。同时，通过引入动量项的方法，明显减缓了粒子后期进化过程中产生的震荡，同时加快了粒子进化的速度，最终使得IPSO算法训练速度较传统的PSO算法，能更加快速地完成收敛，减少训练时间。

图1 4种算法的训练时间Fig．1 Training time of four algorithms

图2 4种算法的泛化时间Fig．2 Testing time of four algorithms

如图3所示，本文利用表1所示训练样本和测试样本，对比验证4种算法的分类准确率。误差率计算公式为

如图所示，IPSO-SVM的准确率都比另外3种算法高，而且与PSO-SVM相比，IPSO-SVM准确率提高了3％～5％。因此，从模型的训练时间和分类的准确率来看，IPSO-SVM都有一定的优势。

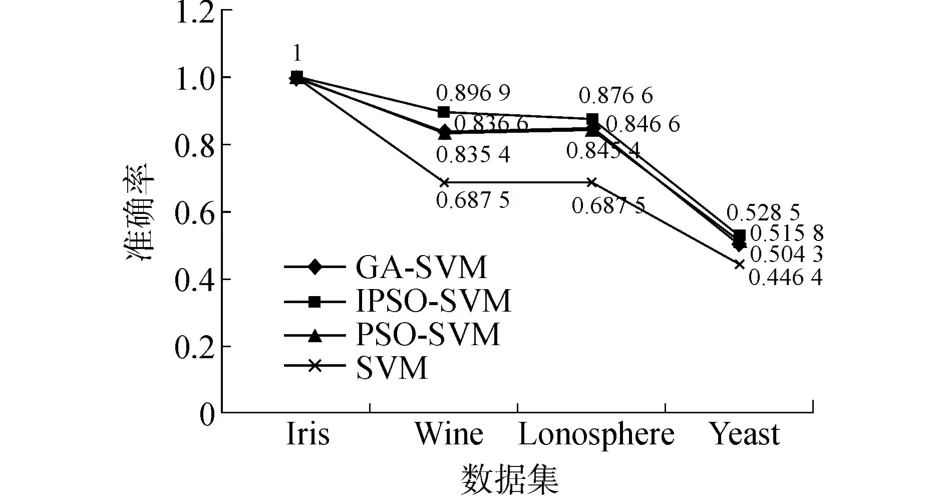
图3 4种算法的准确率对比图Fig．3 The precisions of four algorithms

4 IPSO-SVM在矿产资源预测中的应用

遥感图像分类是实现矿产资源预测的关键技术，本文以秘鲁南部的实验区为例进行矿产资源评价预测的研究。选择遥感图像的大小为8 832× 6 988像素，图像中有部分已知的大型铜矿和小型铜矿区。通过对遥感图像多波段影像的分析，以及地质专家对此处成矿因素的地质解译，选择6组成矿要素（铁染蚀变、羟基蚀变、主线性构造、次线性构造、环形构造和地层信息）作为分类的特征变量，如图4中所示，部分示矿信息已在图中标出。采用C#语言开发了矿产资源评价预测系统，并将IPSOSVM算法应用到该系统中。

图4 地质解译图Fig．4 Geological interpretation graph

如图5～7所示，分别应用PSO-SVM和IPSOSVM算法对实验靶区进行了矿产资源的预测与评价，实验靶区的已知矿点都显示准确，而且通过对两种矿产资源预测图进行对比，基于IPSOSVM算法的矿产评价图所显示的信息量更少，表示其预测出矿产资源的可能分部区域更少，结果更加精确，因此与PSO-SVM算法相比，IPSO-SVM算法提高了资源预测的准确度，从实践中验证了该算法的有效性。

图5 已知矿点分布图Fig．5 Distribution of known mineralization points

图6 基于PSO-SVM算法的矿产资源预测图Fig．6 Distribution of mineral resources based on PSO-SVM

图7 基于IPSO-SVM算法的矿产资源预测图Fig．7 Distribution of mineral resources based on IPSO-SVM

5 结论

SVM模型参数的选择是影响其分类效果的重要因素，采用PSO算法优化SVM模型参数是常用的方法之一。但PSO算法存在容易陷入局部极小值、后期震荡严重的问题。

1）首先利用混沌序列初始化例子初始位置，然后在简化的PSO公式的基础上，通过借鉴多个粒子的经验使得每个粒子获得更多的信息，通过增加扰动项来提高粒子的多样性以避免“过早熟”现象；同时也通过引入动量项来缓解寻优过程中的震荡问题。

2）采用改进的PSO算法（IPSO算法）来改进SVM模型的参数，与SVM、PSO-SVM和GA-SVM相比，本文所提出的IPSO-SVM在分类时间和分类准确率上均有一定优势。

3）将IPSO-SVM算法应用到基于遥感影像的矿产资源预测中，与PSO-SVM相比，IPSO-SVM算法提高了资源预测的准确度，在实践中验证了算法的有效性。

在具体的应用中，IPSO算法参数（如c1、c2和c3等）往往需要依靠经验来设置，针对具体应用问题，如何自适应地调整参数值是需要继续研究的另一个问题。

［1］张鑫源，胡晓敏，林盈．遗传算法和粒子群优化算法的性能对比分析［J］．计算机科学与探索，2014，8（1）:91-102．ZHANG Xinyuan，HU Xiaomin，LIN Ying．Comparisons of genetic algorithm and particle swarm optimization［J］．Journal of frontiers of computer science and technology，2014，8（1）:91-102．

［2］SHI Yuhui，EBERHART R C．A modified particle swarm optimizer［C］／／Proceedings of The 1998 IEEE International Conference on Evolutionary Computation．Anchorage，AK，USA:IEEE，1998:69-73．

［3］SHI Yuhui，EBERHART R C．Fuzzy adaptive particle swarm optimization［C］／／Proceedings of the 2001 Congress on Evolutionary Computation．Seoul，South Korea:IEEE，2001: 101-106．

［4］王俊伟，汪定伟．粒子群算法中惯性权重的实验与分析［J］．系统工程学报，2005，20（2）:194-198．WANG Junwei，WANG Dingwei．Experiments and analysis on inertia weight in particle swarm optimization［J］．Journal of systems engineering，2005，20（2）:194-198．

［5］SUGANTHAN P N．Particle swarm optimizer with neighborhood operator［C］／／Proceedings of the Congress on Evolutionary Computation．Washington，DC，USA，1999:1958-1962．

［6］RATNAWEERA A，HALGAMUGE S K，WATSON H C．Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients［J］．IEEE transactions on evolutionary computation，2004，8（3）:240-255．

［7］于立君，陈佳，刘繁明，等．改进粒子群算法的PID神经网络解耦控制［J］．智能系统学报，2015，10（5）:699-704．YU Lijun，CHEN Jia，LIU Fanming，et al．An improved particle swarm optimization for PID neural network decoupling control［J］．CAAI transactions on intelligent systems，2015，10（5）:699-704．

［8］KENNEDY J，MENDES R．Population structure and particle swarm performance［C］／／Proceedings of Congress on Evolutionary Computation．Honolulu，HI，USA:IEEE，2002: 1671-1676．

［9］潘峰，陈杰，甘明刚，等．粒子群优化算法模型分析［J］．自动化学报，2006，32（3）:368-377．PAN Feng，CHEN Jie，GAN Minggang，et al．Model analysis of particle swarm optimizer［J］．Acta automatica sinica，2006，32（3）:368-377．

［10］HU Xiaohui，EBERHART R C．Multiobjective optimization using dynamic neighborhood particle swarm optimization［C］／／Proceedings of the 2002 IEEE International Congress on Evolutionary Computation．Honolulu，HI，USA: IEEE，2002:1677-1681．

［11］VAN DEN BERGH F，ENGELBRECHT A P．Training product unit networks using cooperative particle swarm optimisers［C］／／Proceedings of IEEE International Joint Conference on Neural Networks．USA:IEEE，2001:1-9．

［12］ANGELINE P J．Evolutionary optimization versus particle swarm optimization:philosophy and performance differences［M］／／PORTO V W，SARAVANAN N，WAAGEN D，et al．Evolutionary Programming VII．Berlin Heidelberg:Springer，1998:601-610．

［13］高鹰，谢胜利．基于模拟退火的粒子群优化算法［J］．计算机工程与应用，2004（1）:47-50．GAO Ying，XIE Shengli．Particle swarm optimization algorithms based on simulated annealing［J］．Computer engineering and applications，2004（1）:47-50．

［14］肖燕彩，陈秀海，朱衡君．遗传支持向量机在电力变压器故障诊断中的应用［J］．上海交通大学学报，2007，41（11）:1878-1881，1886．XIAO Yancai，CHEN Xiuhai，ZHU Hengjun．The application of genetic support vector machine in power transformer fault diagnosis［J］．Journal of Shanghai Jiaotong University，2007，41（11）:1878-1881，1886．

［15］胡旺，李志蜀．一种更简化而高效的粒子群优化算法［J］．软件学报，2007，18（4）:861-868．HU Wang，LI Zhishu．A simpler and more effective particle swarm optimization algorithm［J］．Journal of software，2007，18（4）:861-868．

［16］郭广寒，王志刚．一种改进的粒子群算法［J］．哈尔滨理工大学学报，2010，15（2）:31-34．GUO Guanghan，WANG Zhigang．A modified particle swarm optimization［J］．Journal of Harbin university of science and technology，2010，15（2）:31-34．

A support vector machine based on an improved particle swarm optimization algorithm and its application

WANG Zhenwu，SUN Jiajun，YIN Chengfeng
（School of Mechanical Electronic＆Information Engineering，China University of Mining and Technology，Beijing 100083，China）

The traditional particle swarm optimization（PSO）algorithm has two types of defects，i．e．，easily falling into the local minima and severe shock in the later stages．To address these problems，this paper proposes an improved PSO（IPSO）algorithm，which introduces a chaotic sequence to initialize the positions of the particle swarm，and optimizes it from two aspects based on a simplified PSO mathematical model．This paper used IPSO to optimize the model parameters of a support vector machine（SVM）．The simulation experiment results proved that compared with SVM，PSO-SVM，and genetic algorithm optimized SVM（GA-SVM），the improved PSO optimized SVM（IPSO-SVM）has higher classification accuracy．Compared with PSO-SVM，IPSO-SVM increased the accuracy by 3％～5％，and compared with PSO-SVM and GA-SVM，the training and testing time was obviously reduced．Finally，the IPSO-SVM algorithm was applied to the classification of remote sensing images；the results proved that IPSO-SVM offers better classification solutions than PSO-SVM．

particle swarm optimization algorithm；chaotic sequence；support vector machine；remote sensing images

10．11990／jheu．201601005

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．036．html

TP301．6

A

1006-7043（2016）12-1728-06

王振武，孙佳骏，尹成峰．改进粒子群算法优化的支持向量机及其应用［J］．哈尔滨工程大学学报，2016，37（12）:1728-1733．

2016-01-05．

2016-09-28．

国家自然科学基金项目（61302157）；国家高技术研究发展计划重大专项（2012AA12A308）；核设施退役及放射性废物治理科研项目（FZ1402-08）；北京市高等学校青年英才计划（YETP0939）；中央高校基本科研业务费项目（2009QJ-11）．

王振武（1978-），男，副教授．

王振武，E-mail:wangzhenwu＠126．com．

WANG Zhenwu，SUN Jiajun，YIN Chengfeng．A support vector machine based on an improved particle swarm optimization algorithm and its application［J］．Journal of Harbin Engineering University，2016，37（12）:1728-1733．