基于密度背景纯化的高光谱异常检测算法

赵春晖，王鑫鹏，闫奕名

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

基于密度背景纯化的高光谱异常检测算法

赵春晖，王鑫鹏，闫奕名

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

在高光谱图像异常检测中，背景存在异常像元会造成背景统计信息失真，这将导致检测结果具有较高的虚警率。针对此问题，本文提出了一种基于密度背景纯化的异常检测算法。首先计算背景中每个像元的密度；然后根据高光谱图像中背景密度远大于异常密度的特性，利用最大类间方差法将异常从背景中分离；最后，将纯化后的背景用于统计信息的估计，通过RX检测算法（Reed-Xiaoli detector，RXD）对高光谱图像进行检测。为验证算法的有效性，利用两组真实的高光谱数据进行仿真实验。实验结果表明与RXD比，所提算法在两组数据下的曲线下面积值分别提高了0．024 6和0．008 6。与当前的异常检测算法相比：所提算法有较好的接收机工作特性曲线。

高光谱图像；遥感；异常检测；密度；纯化；RX检测算法；最大类间方差法；接收机工作特性

高光谱图像是一种图谱合一的新型遥感数据，具有很高的光谱分辨率。借助其丰富的光谱信息，可以通过目标检测或异常检测算法识别高光谱图像中的低概率地物。异常检测在目标先验知识未知的情况下，通过分析背景与异常目标的光谱差异，直接检测出异常点。这对背景和目标分布未知的检测识别具有重要意义。

经典的异常检测算法是Reed等［1］基于广义似然比检验提出的RX算法。它基于两点假设:背景服从多维高斯分布模型和异常像元在高光谱图像中低概率存在。由于在实际应用中高光谱图像通常包含多种地物［2］，同时受阴影、光照效果、大气干扰或同谱异物的影响，背景复杂多变。并且，高光谱图像中存在同背景像元相似度很高的亚像元级异常目标［3］，增加了背景复杂性。因此多维高斯分布模型不能全面描述真实背景地物的分布特性。Smetek等［4］指出只要存在0．5％的数据污染就会造成协方差失真，高光谱图像背景的复杂性造成了统计信息的失真，导致RX检测算法存在较高的虚警率。针对此问题，文献［5-8］通过背景纯化将异常分离，使背景更为符合多维高斯分布模型，得到更为准确的背景统计信息（背景协方差与均值向量），降低了RX检测的虚警率。Gorelnik等［5］通过聚类方法分割图像，将背景所在类的像元用于计算协方差矩阵和均值向量，得到了更准确的背景统计信息。而文献［6-7］通过RXD迭代方式对背景纯化，获得更准确的背景统计信息，降低了检测虚警率。Billor等［6］通过RXD迭代方式对背景纯化，并引入校正因子增强背景纯化的稳健性，提出了BACON（blocked adaptive computationally efficient outlier nominators）。针对BACON初始背景存在较多异常像元的问题，Du等［7］通过随机选择像元构建初始背景，降低了初始背景中异常所占的比例，并且融合多次实验结果增强了检测效果，提出了RSAD（random-selectionbased anomaly detector）。不同于BACON和RSAD的迭代方式，Gao等［8］提出的PAD（probabilistic anomaly detector）首先通过概率统计方式自适应获得阈值，依据RXD检测结果，将高光谱图像分割为异常和背景两部分，然后利用异常和背景两部分的统计信息，将像元归属于背景和异常的程度之差作为判别依据。

通过背景纯化可以去除背景中的异常数据，得到更准确的背景统计信息，从而有效的降低虚警率。所以对背景纯化的研究是十分有必要的。由于异常在高光谱图像中稀疏分布，且异常像元数目远少于背景像元数目，通过计算像元的密度可以有效分离背景中的异常。据此本文提出了一种基于密度背景纯化的异常检测算法（density background refinement based anomaly detector，DBRAD），通过将背景纯化方法引入RXD中，降低了RXD的虚警率。

1 基于密度背景纯化的异常检测算法

1．1 RX检测算法

RX检测算法是一种基于广义似然比检测的异常检测算法，可以通过单一的阈值来维持所期望的虚警率。RX算法可以看作一个二元信号检测问题。使H0表示目标不存在，H1表示目标存在，二元假设表示如下

式中:x表示高光谱图像像元，n表示背景噪声向量，s表示目标光谱向量。定义为包含N个像元的L×N的背景矩阵，第i个像元表示为表示高光谱图像波段数。假设背景和目标分布具有相同的协方差和不同的均值，分别服从多维高斯分布和为背景Xb的均值，K为协方差矩阵。根据以上假设，可以获得背景和目标的概率密度函数:

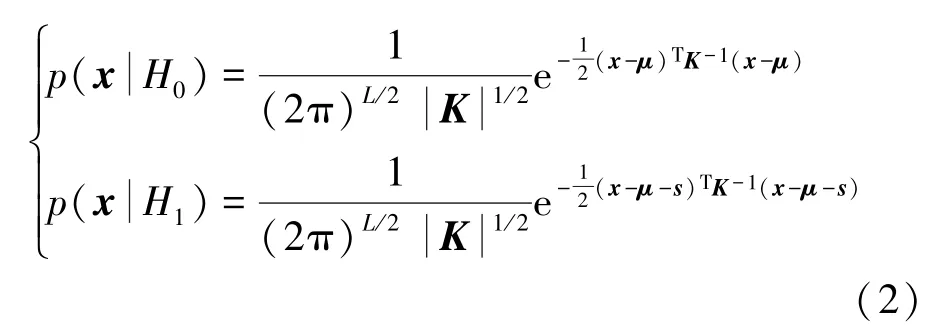
当样本数N趋于无穷时，进一步简化为

从式（4）可以看出RX判别式与马氏距离有着相同的形式，可以看作像元到背景集合的协方差距离。本质上，RXD可以看作主成分分析的逆过程［9］，通过对协方差矩阵K进行奇异值分解，可以将RX判别式表示成主成分特征值加权的欧几里德范数的形式。异常目标与协方差矩阵的小特征值对应，而特征值越小，RX检测结果越大，这是RX算法能有效地应用于异常目标检测的原因。

根据构造背景方式不同，RX检测算法分为局部RX检测算法（local RXD，LRXD）［10］和全局RX检测算法（global RXD，GRXD）。GRXD采用图像的所有像元作为背景，而LRXD基于滑动同心双层窗模型选择检测像元的局部近邻对背景的协方差和均值等参数进行估计。同心双层窗模型分为外窗和内窗，外窗内的像元集合作为背景，内窗作为保护窗将检测像元与背景分离。窗口的大小由感兴趣目标的尺寸决定［8］。由于异常像元可能存在于构造的背景中，直接将图像的所有像元或外窗中的像元作为背景计算协方差和均值是不准确的，这会造成较大的虚警率。通过背景纯化可以将异常像元从初始的背景中分离，从而计算得到更准确的背景统计信息，降低虚警率。由于LRXD能更好地检测图像中的小目标，且局部背景更符合多维高斯分布模型，本文将密度背景纯化方法应用于LRXD中。

1．2 密度背景纯化方法

密度指单位空间中物体的数量。如图1（a）所示，以像元p为球心，以一定距离为半径构造超球体，将像元p的密度定义为:超球体内像元的数目与该超球体体积的比值。其函数表示为

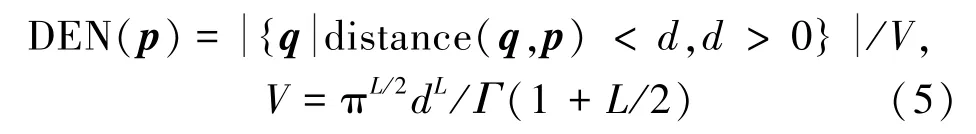
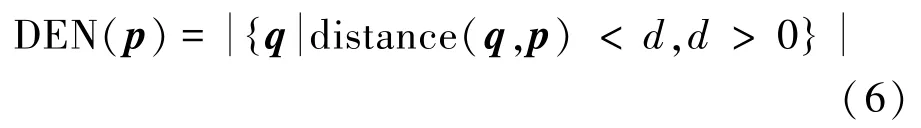
即像元密度可以简化为求超球体内像元数目［11］。由于异常在高光谱图像中稀疏分布，且异常像元数目远少于背景像元数目，所以背景像元的密度远大于异常像元的密度，如图1（b）所示。

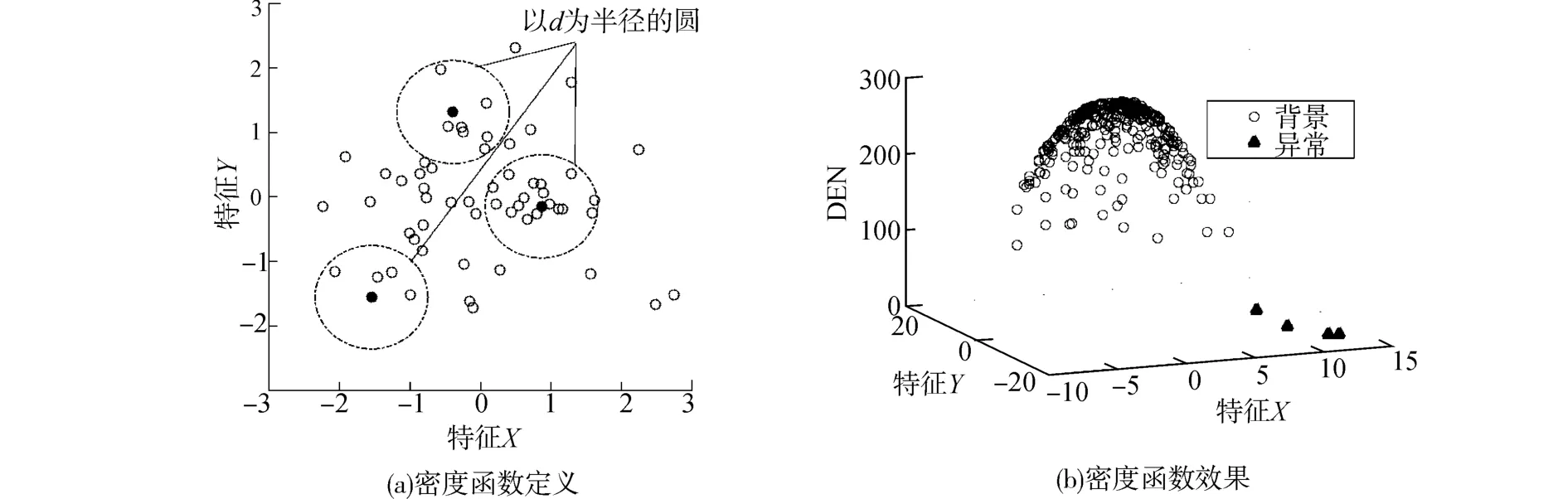
图1 密度函数定义和效果示意图Fig．1 Illustration of the density definition and the result of the density function

本文选用欧氏距离计算像元间距，将高光谱数据归一化，则像元间的最大距离为为高光谱图像波段数。计算像元间距时将其除以归一化，以便之后半径d的选取。

半径d的取值会对像元密度的计算产生较大影响:若d取值过大，则易将背景与异常混合于超球体中，这时无论背景像元或异常像元都具有较大的密度；若d取值过小则会对像元过分割，像元密度过小，同样会造成异常与背景的密度相近的情况。所以d取值过大过小都会对异常分离造成不利影响。由于同类地物的像元聚合程度很高，同类地物的像元可以聚集于一个小半径的超球体中，本文设定的该半径在像元间距最大值的1％～5％，即d的取值区间为［0．01，0．05］。

确定d的取值后，根据式（6）计算背景矩阵Xb各个像元xi的密度deni，得到背景像元密度向量然后根据背景像元密度大小，通过两次分割将异常分离。初次分割通过设定一定的比例分割出稳健的背景:设异常在初始背景中的比例不超过10％［11］，确定背景中密度最大的80％的像元为背景像元，而异常存在于剩余的20％的像元中。如式（7），将这20％像元记为Xs，其密度记为dens。

二次分割通过最大类间方差法将Xs中的异常分离。最大类间方差法［12］是一种自适应的阈值确定方法，又叫大津法，简称Otsu，常用于图像分割。它按图像的灰度特性，将图像分成背景和目标两部分。背景和目标之间的类间方差越大，说明构成图像的两部分的差别越大，错分会导致两部分差别变小。因此，使类间方差最大的分割意味着错分概率最小。本文将Otsu应用于密度向量的分割。首先将dens灰度化:

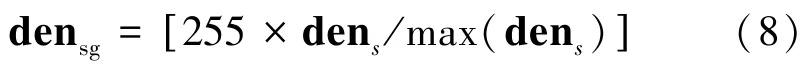
式中:max（·）表示其中元素的最大值，[·]表示根据四舍五入取整。然后遍历灰度值（[0，255]区间内的整数），将其作为阈值将densg分成异常和背景两部分。计算两部分间的方差，当两部分间的方差最大时记录该灰度值th:

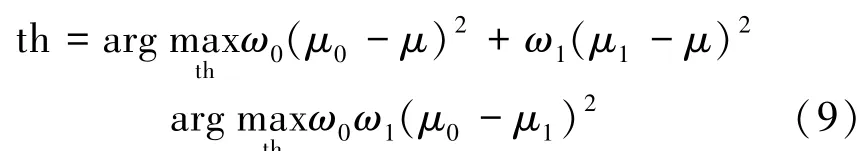
式中:ω0表示densg中小于th的元素所占比例，ω1表示densg中不小于th的元素所占比例；μ0、μ1、μ分别为densg中小于th的元素的均值、densg中大于等于th的元素的均值、densg的均值。当存在多个灰度值满足条件时，取它们的平均值作为th。接着，将th去灰度化，得到分割阈值thf:

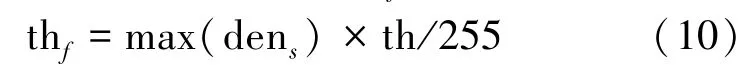
最后如式（11），将den中不小于thf的元素对应的像元判别为背景像元，更新Xb:

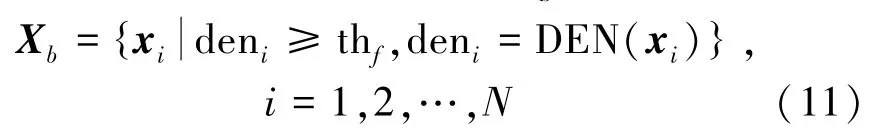
DBRAD算法通过计算背景像元密度将异常从背景中分离，最后将纯化后的背景统计信息用于LRXD中进行检测。DBRAD算法的具体步骤如下所示:

1）利用双层窗模型，获得当前检测像元xi对应的背景矩阵Xb。

2）根据式（6）～（11）纯化背景，更新Xb。

3）根据更新后的Xb计算背景均值μ和协方差矩阵K，代入式（4）计算，得到像元判别值。

4）设定阈值，将判别值大于阈值的像元判为异常。

2 实验及分析

实验利用两组高光谱图像数据（美国圣地亚哥海军基地数据和SpecTIR数据）对DBRAD算法的检测性能进行测试。

2．1 美国圣地亚哥海军基地数据

美国圣地亚哥海军基地数据［13］由AVIRIS成像仪获得，图像大小为400×400，图像覆盖了从可见光到近红外的连续光谱范围，共有224波段，去除水吸收带和低信噪比的波段后，剩下126个波段用于仿真实验。如图2所示，截取了该图像的一部分区域用于仿真实验。截取图像的大小为100×100，包含38个待检测目标。

图2 圣地亚哥海军基地数据的第60波段图像及目标分布图Fig．2 The sixtieth band image and targets distribution for the Santiago naval base data

实验在Intel Core i5-4210M主频2．60G CPU，8G内存，Matlab 2014b环境下进行。

在对高光谱数据进行归一化后，根据感兴趣目标大小，将外窗大小设为15×15，内窗大小设为5× 5。为了验证本文算法的效果，选择原始算法LRXD，最佳的迭代算法RSAD和最近提出的PAD算法作为对比算法。

将接收机工作特性（receiver operating characteristic，ROC）作为性能评价的方法［14-15］。高光谱检测领域中，将检测到的真实目标像素个数与实际目标个数比值定义为检测率Pd，将检测到的虚警像素个数同整幅高光谱图像像素总数的比值定义为虚警率Pf。

图3（a）给出了取不同值（0．05，0．03，0．01）时DBRAD的ROC曲线比较。可以看出当d取值为0．01时，检测效果最好，在相同虚警率下具有较高的检测率。但存在d取值不同时ROC曲线差距较大的问题。图3（b）给出了DBRAD（d=0．01）同LRXD、RSAD、PAD算法的ROC曲线比较。可以看出DBRAD的ROC曲线变化更快，检测率高于其他算法。

表1给出了d取不同值时DBRAD的曲线下面积（area under the ROC curve，AUC）。表2给出了LRXD、RSAD、PAD和DBRAD的AUC比较。综合表1和表2可以发现，d取0．05、0．03或0．01时DBRAD的AUC都大于其他算法。

从检测结果二值图可以看出，相对PAD、RSAD、LRXD有些目标检测结果不够清晰完整，DBRAD可以有效的检测出38个异常目标且虚警点更少。

通过以上对比分析，虽然存在因d取值不同导致DBRAD检测效果有较大差异的问题，但是在时，DBRAD同其他算法相比也有较好的检测效果。说明通过密度纯化可以有效抑制异常干扰，提高检测性能。

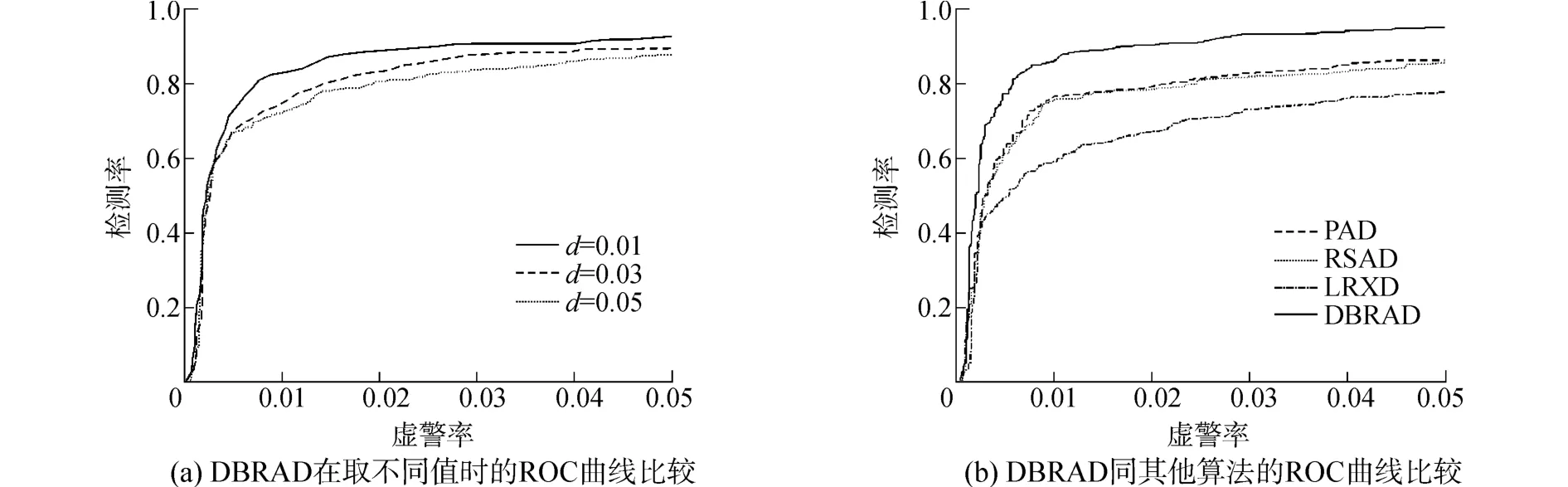
图3 美国圣地亚哥海军基地数据的ROC曲线比较Fig．3 ROC curves comparison for the Santiago naval base data

2．2 SpecTIR数据

SpecTIR数据采集于SpecTIR高光谱机载曼彻斯特实验［16］，由ProSpecTIR-VS2成像仪拍摄于2010年7月29日。SpecTIR数据包含360个波段，波段范围390～2 450 nm，光谱分辨率5 nm，空间分辨率1 m。如图3所示，选取大小为100×100的区域用于实验。该区域包含不同尺寸（9、4、0．25 m2）和材质（棉或聚酯纤维）的布料，将其作为检测目标。

图6（a）给出了d取不同值（0．05、0．03和0．01）时DBRAD的ROC曲线比较。当d=0．05与d= 0．03时检测效果相近，但明显优于d=0．01的情况。图6（b）给出了DBRAD（d=0．03）同LRXD、RSAD、PAD算法的ROC曲线比较。可以看出虽然DBRAD在虚警率区间［0．015，0．023］内检测率相比PAD较低，但DBRAD的ROC曲线在低虚警率区间［0，0．01］变化率更高且检测率远高于其他算法，说明DBRAD能更快更多地检测到目标，所以DBRAD整体效果还是最好的。

表1 DBRAD在d取不同值时的曲线下面积Table 1 AUC of DBRAD with different

表2 LRXD、RSAD、PAD和DBRAD的曲线下面积Table 2 AUC of DBRAD，LRXD，RSAD and PAD

图4 圣地亚哥海军基地数据的检测结果二值图Fig．4 Detection results for the Santiago naval base data

图5 SpecTIR数据第60波段图像及目标分布图Fig．5 The sixtieth band image and targets distribution for the SpecTIR data

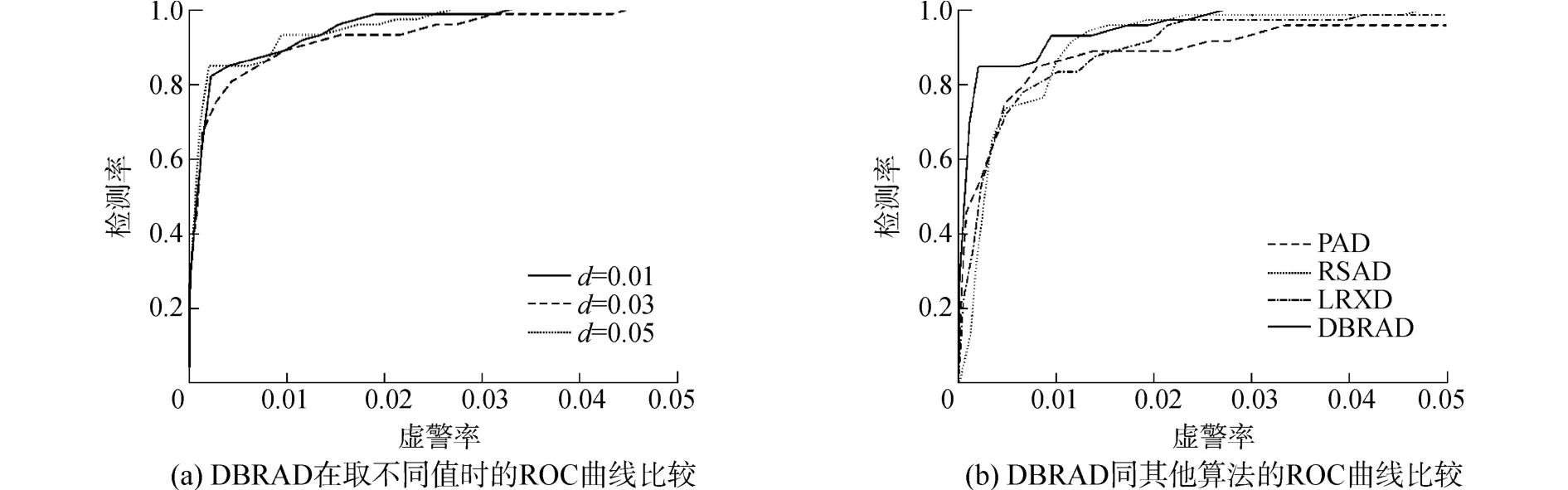
图6 SpecTIR数据的ROC曲线比较Fig．6 ROC curves comparison for the SpecTIR data

表3给出了d取不同值时DBRAD的AUC比较。表4给出了LRXD、RSAD、PAD和DBRAD的AUC比较。综合表3和表4可以发现，d取0．05、0．03或0．01时DBRAD的AUC都大于其他算法，且彼此AUC差距较小。

从检测结果二值图可以看出，相对LRXD、PAD和RSAD、DBRAD可以更清晰完整地检测出目标。

表3 DBRAD在d取不同数值时的曲线下面积Table 3 AUC of DBRAD with different d

表4 LRXD、RSAD、PAD和DBRAD的曲线下面积Table 4 AUC of DBRAD，LRXD，RSAD and PAD

图7 SpecTIR数据的检测结果二值图Fig．7 Detection results for the SpecTIR data

3 结论

1）将密度背景纯化方法引入RXD中用以去除背景中的异常像元，提出了基于密度背景纯化的异常检测算法（DBRAD）。

2）对于圣地亚哥海军基地数据和SpecTIR数据，DBRAD的AUC值比RXD分别提高了0．024 6和0．008 6。同时，从ROC曲线可以看出DBRAD相比于其他算法有较高的检测率。这说明，密度背景纯化方法有效抑制了异常点对背景数据的干扰，使背景协方差和均值等参数更加准确，降低了虚警率。

3）在计算密度时，需要人为设定半径值。对于两幅高光谱数据，在不同半径选择下DBRAD最大AUC差值为0．008 8和0．001 2。这说明人为选择半径值可能会对最后的检测效果造成较大影响。如何自适应选取半径将是下一步研究的重点。

［1］REED I S，YU X．Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution［J］．IEEE transactions on acoustics，speech，and signal processing，1990，38（10）:1760-1770．

［2］HUCK A，GUILLAUME M．Asymptotically CFAR-unsupervised target detection and discrimination in hyperspectral images with anomalous-component pursuit［J］．IEEE transactions on geoscience and remote sensing，2010，48（11）:3980-3991．

［3］CHANG C I，HEINZ D C．Constrained subpixel target detection for remotely sensed imagery［J］．IEEE transactions on geoscience and remote sensing，2000，38（3）:1144-1159．

［4］SMETEK T E，BAUER K W．Finding hyperspectral anomalies using multivariate outlier detection［C］／／Aerospace Conference，2007 IEEE．Big Sky，MT，USA:IEEE，2007:1-24．

［5］GORELNIK N，YEHUDAI H，ROTMAN S R．Anomaly detection in non-stationary backgrounds［C］／／Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing:Evolution in Remote Sensing．Reykjavìk，Iceland:IEEE，2010:1-4．

［6］BILLOR N，HADI A S，VELLEMAN P F．BACON:blocked adaptive computationally efficient outlier nominators［J］．Computational statistics＆data analysis，2000，34（3）:279-298．

［7］DU Bo，ZHANG Liangpei．Random-selection-based anomaly detector for hyperspectral imagery［J］．IEEE transactions on geoscience and remote sensing，2011，49（5）:1578-1589．

［8］GAO Lianru，GUO Qiandong，PLAZA A，et al．Probabilistic anomaly detector for remotely sensed hyperspectral data［J］．Journal of applied remote sensing，2014，8（1）:083538．

［9］VELASCO-FORERO S，CHEN M，GOH A，et al．Comparative analysis of covariance matrix estimation for anomaly detection in hyperspectral images［J］．IEEE journal of selected topics in signal processing，2015，9（6）:1061-1073．

［10］MOLERO J M，GARZÓN E M，GARCÍA I，et al．Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data［J］．IEEE journal of selected topics in applied earth observations and remote sensing，2013，6（2）:801-814．

［11］LOU Chen，ZHAO Huijie．Local density-based anomaly detection in hyperspectral image［J］．Journal of applied remote sensing，2015，9（1）:095070．

［12］OTSU N．A threshold selection method from gray-level histograms［J］．IEEE transactions on systems，man，and cybernetics，1979，9（1）:62-66．

［13］赵春晖，李晓慧，朱海峰．空间4-邻域稀疏表示的高光谱图像目标检测［J］．哈尔滨工程大学学报，2013，34（9）:1171-1178．ZHAO Chunhui，LI Xiaohui，ZHU Haifeng．Hyperspectral imaging target detection algorithm based on spatial 4 neighborhoods for sparse representation［J］．Journal of Harbin Engineering University，2013，34（9）:1171-1178．

［14］MOLERO J M，GARZÓN E M，GARCÍA I，et al．Anomaly detection based on a parallel kernel RX algorithm for multicore platforms［J］．Journal of applied remote sensing，2012，6（1）:061503．

［15］赵春晖，李晓慧，田明华．采用主成分量化和密度估计期望最大聚类的高光谱异常目标检测［J］．光子学报，2013，42（10）:1224-1230．ZHAO Chunhui，LI Xiaohui，TIAN Minghua．Hyperspectral imaging abnormal target detection algorithm using principal component quantization and density estimation on EM clustering［J］．Acta photonica sinica，2013，42（10）:1224-1230．

［16］HERWEG J A，KEREKES J P，WEATHERBEE O，et al．SpecTIR hyperspectral airborne Rochester experiment data collection campaign［C］／／Proceedings of SPIE 8390，Algorithms and Technologies for Multispectral，Hyperspectral，and Ultraspectral Imagery XVIII．Baltimore，Maryland，USA:SPIE，2012:839028．

Density background refinement-based anomaly detection algorithm for hyperspectral images

ZHAO Chunhui，WANG Xinpeng，YAN Yiming
（College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China）

In anomaly detection in hyperspectral images，a background anomaly distorts the background statistical information，leading to a high false-alarm rate．Here a density background refinement-based anomaly detector is proposed to solve this problem．The density of each background pixel was calculated first．Then，considering that the background density is much greater than the density of an anomaly in hyperspectral images，anomalies were separated from background using Otsu′s method．Finally，the image was detected with a Reed-Xiaoli detector（RXD）using statistical information on the refined background．To validate the effectiveness of the proposed algorithm，experiments were conducted on two real hyperspectral data sets．The results show that the proposed algorithm′s areaunder-curve values are 0．024 6 and 0．008 6 larger than RXD for the two data，respectively，and that it shows better receiver operating characteristics compared with existing anomaly detection algorithms．

hyperspectral image；remote sensing；anomaly detection algorithm；density；refinement；RX detector；Otsu′s method；receiver operating characteristic

10．11990／jheu．201511073

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．038．html

TP751．1

A

1006-7043（2016）12-1722-06

赵春晖，王鑫鹏，闫奕名．基于密度背景纯化的高光谱异常检测算法［J］．哈尔滨工程大学学报，2016，37（12）:1722-1727．

2015-11-28．

2016-09-28．

国家自然科学基金项目（61571145，61601135）；黑龙江省自然科学基金项目（ZD201216）；哈尔滨市优秀学科带头人基金项目（RC2013XK0 09003）；中央高校基本科研业务费专项基金项目（GK2080260139）．

赵春晖（1965-），男，教授，博士生导师．

赵春晖，E-mail:zhaochunhui＠hrbeu．edu．cn．

ZHAO Chunhui，WANG Xinpeng，YAN Yiming．Density background refinement-based anomaly detection algorithm for hyperspectral images［J］．Journal of Harbin Engineering University，2016，37（12）:1722-1727．