广义剖分冠点图的邻接特征多项式

卢鹏丽，武雨末

（兰州理工大学计算机与通信学院，甘肃兰州730050）

广义剖分冠点图的邻接特征多项式

卢鹏丽，武雨末

（兰州理工大学计算机与通信学院，甘肃兰州730050）

冠图是由图G与图H经过图操作得到的组合图，已经有一些冠图被定义及研究。但是现有文献中的冠图定义均是将图H进行n次拷贝，得到的图G与图H的各类冠图。将冠图的定义推广为一般化的情形，即将原来n个相同的图H一般化为任意图H1，H2，…，Hn，定义了一类新的广义剖分冠点图。首先在图G的每条边上添加一个新的顶点得到其剖分图S（G）；将V（G）中的第i个顶点与Hi中的所有顶点连接；这样由剖分图S（G）和图H1， H2，…，Hn构造的图称为广义剖分冠点图，记为图应用分块矩阵、矩阵的冠、舒尔补定理等确定了广义剖分冠点图的邻接特征多项式；提出了构造无穷邻接同谱图类的方法且给出了示例。

组合图；广义剖分冠点图；邻接特征多项式；正则图；同谱图

本文只讨论无向简单图。图G= (V（G），E（G）)，其中顶点集和边集分别为V（G）=｛v1，v2，…，vn｝， E（G）=｛e1，e2，…，em｝图G的邻接矩阵记为A（G），由元素aij组成，当顶点vi与vj相邻时为1，否则为0。图G的关联矩阵记为R（G），是由元素bij组成，当顶点vi与边ej相邻时为1，否则为0。顶点vi的度记为dG（i）。图G的度矩阵记为D（G），是对角线上元素为dG（i）的n× n对角矩阵。并且有R（G）R（G）T=A（G）+ D（G）。图G的邻接特征多项式记为

式中:In表示大小为n的单位矩阵。由邻接特征多项式得到的特征值称为邻接特征值，从大到小排序为λn≥λn-1≥…≥λ2≥λ1。拥有相同邻接特征多项式的图叫做A-同谱图［1-3］。

冠图是由两个图，图G与图H经过图操作得到的复杂图。已经有一些类的冠图被定义和研究，如冠边图、冠点图、邻居冠图等。冠图的谱难以计算，对于冠图的研究主要是将其表示为原图的谱并用于实际的计算中。本文扩大了冠点图的范围，定义了广义剖分冠点图并确定了其特征多项式，给出了构造无穷邻接同谱图类的方法及示例。

1 主要引理

计算邻接特征多项式的时候采用了舒尔补定理和矩阵的冠，下面给出相关引理。

引理1（舒尔补定理）［4］:设矩阵A为n×n分块矩阵:

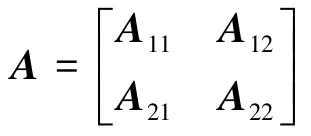
式中:A11与A22为可逆方阵。则

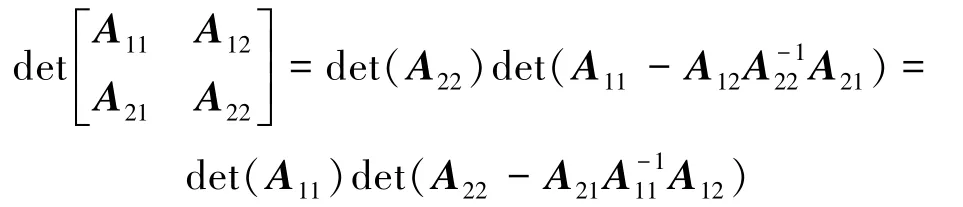
引理2［5-6］:设矩阵M为n×n实对称矩阵，jn是长度为n的全1列向量。则矩阵M的冠，记为ΓM（x），是矩阵(xIn-M)-1的所有元素之和，即

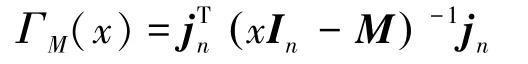
特别地，当矩阵M的每一行元素之和都等于t时:

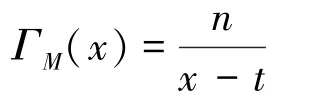
对于n个顶点的r-正则图G，邻接矩阵A（G）的每一行之和都为度r，因此

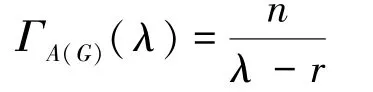
2 广义剖分冠点图的邻接矩阵

冠图是由两个图经过图操作得到的组合图。图G与图H的冠图［7］定义为:将图H复制次，然后将第i个H的所有顶点与V（G）第i个顶点连接，这样由G和｜V（G）｜个H构造的图，称之为图G与图H的冠图。文献［8-12］中定义了各类冠图，如边冠图、邻居冠图、剖分邻居冠图等。但是都是将图H进行n次拷贝，得到的图G与图H的组合图。

本文将冠图的定义推广为一般化的情形，即将原来n个相同的图H一般化为任意图H1，H2，…，Hn，定义了广义剖分冠点图。首先在图G的每条边上添加一个新的顶点得到其剖分图S（G）；将Hi中的所有顶点与V（G）中的第i个顶点连接；这样由剖分图S（G）和图H1，H2，…，Hn构造的图称为广义剖分冠点图，记为图

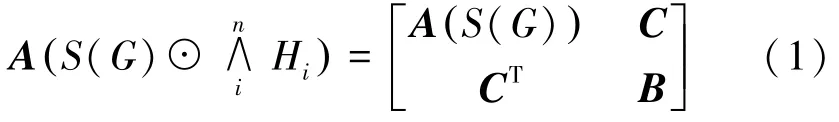
其中，

3 图S（G）☉Hi的邻接特征多项式

定理1设图G有n个顶点m条边。Hi为任意图，i=1，2，…，n。那么

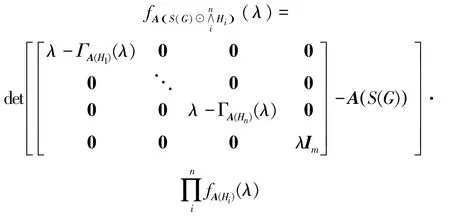
证明:设图Hi有ti个顶点，由式（1）及邻接特征多项式的定义并运用舒尔补定理可知:

记

又因为

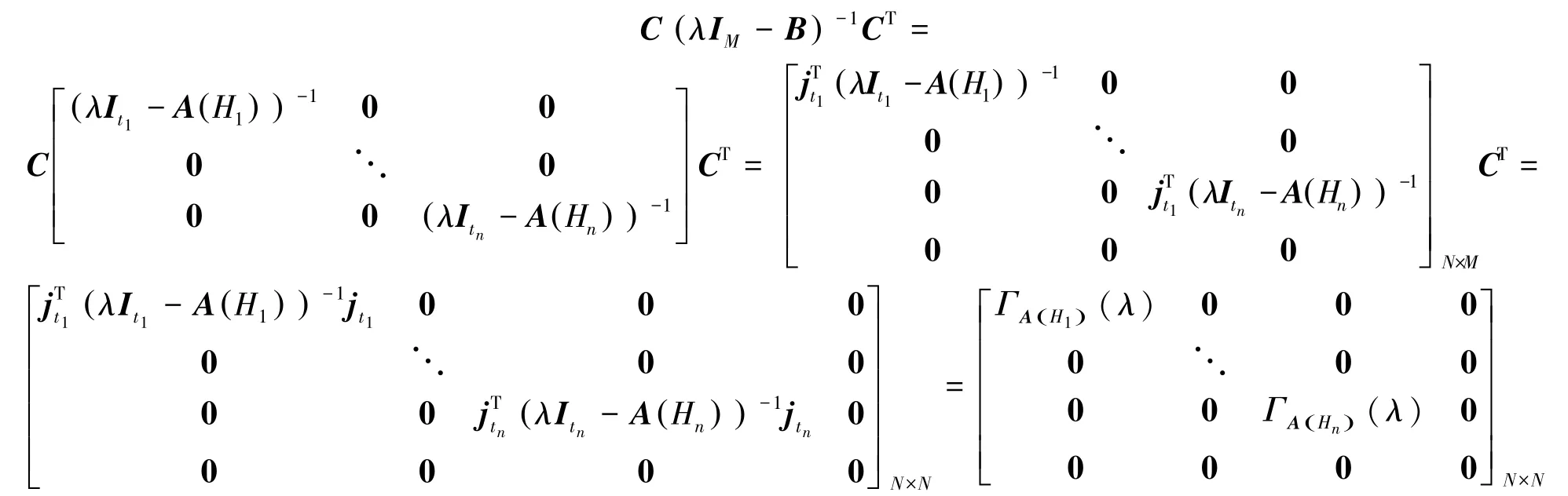
所以

因此，得证。

推论1图G有n个顶点，m条边。若对于图有那么

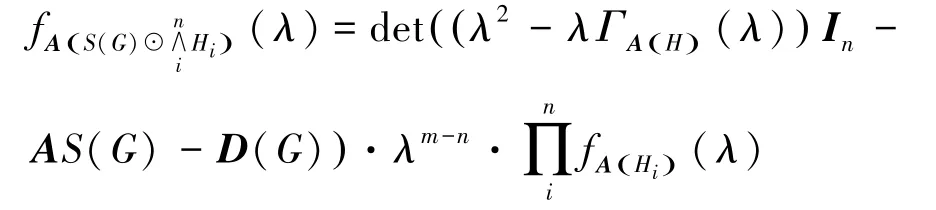
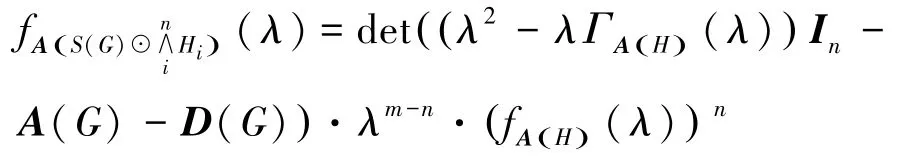
证明:若对于i=1，2，…，n，有ΓA(Hi)（λ）= ΓA(H)（λ），那么设

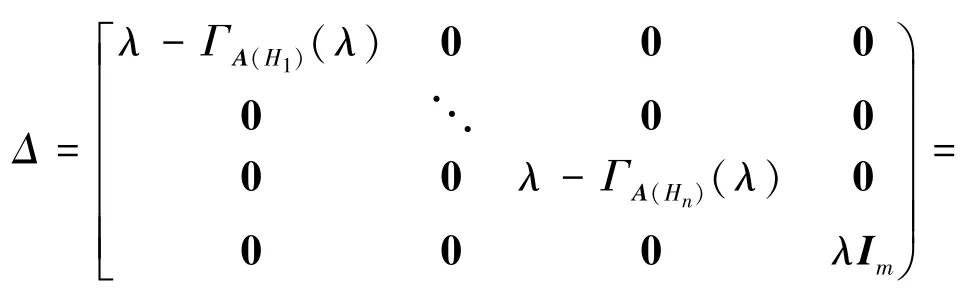
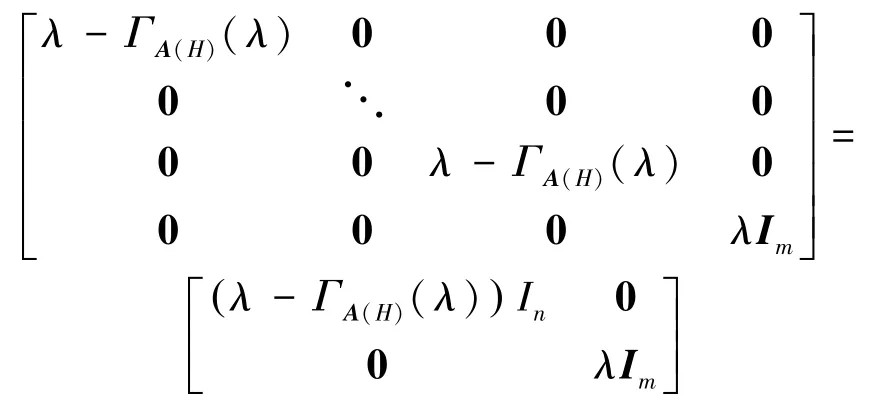
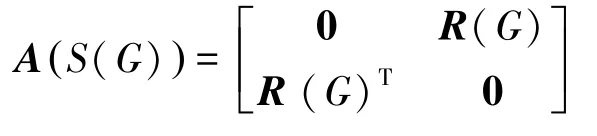
所以

由此，此推论的结果已证得。

由引理2及推论1可以得到下面的推论。

推论2图G有n个顶点，m条边。图H1，H2，…，Hn均为t个顶点的r-正则图，那么

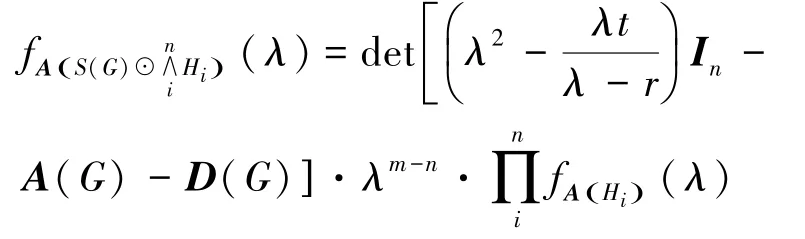
由推论1可得下面的推论。

推论3r-正则图G有n个顶点，m条边，H为一个任意图。设图G的第i个邻接特征值为λi（G），那么图G与n个图H构成的剖分冠点图的邻接特征多项式如下:

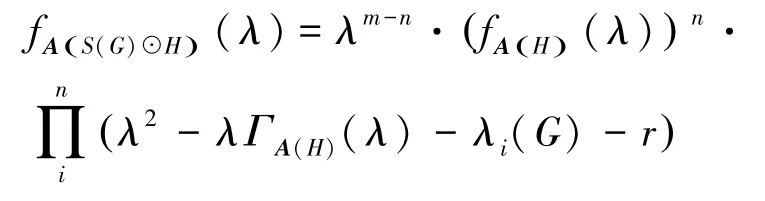
4 广义剖分冠点图的邻接同谱图

推论4G1和G2是两个邻接同谱的r-正则图，若图H1，H2，…，Hn的邻接矩阵的冠相等，即

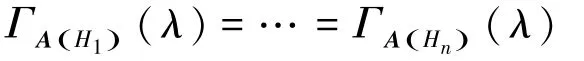
推论5图G有n个顶点。取为一簇邻接同谱图族（其中Hi可有相同的），且那么任取这个邻接同谱图族中大小为n的子集与图G所构成的广义剖分冠点图之间是彼此邻接同谱的。

对于推论5，我们给出如下例子:如图1所示，图G2和图G3是邻接同谱图，其邻接特征多项式均为且它们邻接矩阵的冠值也相等，即

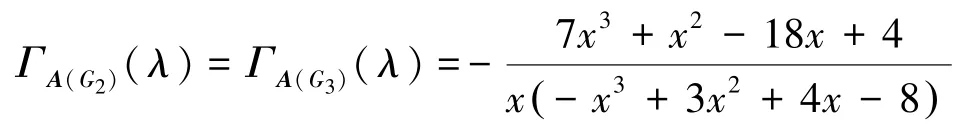
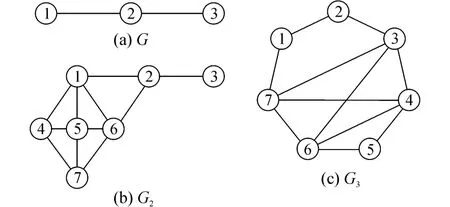
图1 例子中用到的三个图Fig．1 Three graphs used in the example

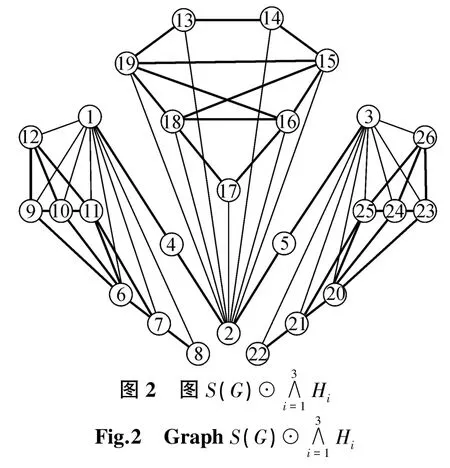
那么取邻接同谱图族｛Hi｜H1=G2，H2=G3，H3=G2，H4=G3，H5=G2，H6=G3｝。任取这个邻接同谱图族中大小为3的子集，即｛H1，H3，H5｝、｛H2，H4，H6｝、｛H1，H2，H3｝、｛H2，H3，H4，｝，与图G所构成的广义剖分冠点图（如图2就是图G与｛H1，H2，H3｝构成的广义剖分冠点图的邻接特征多项式均相等，为

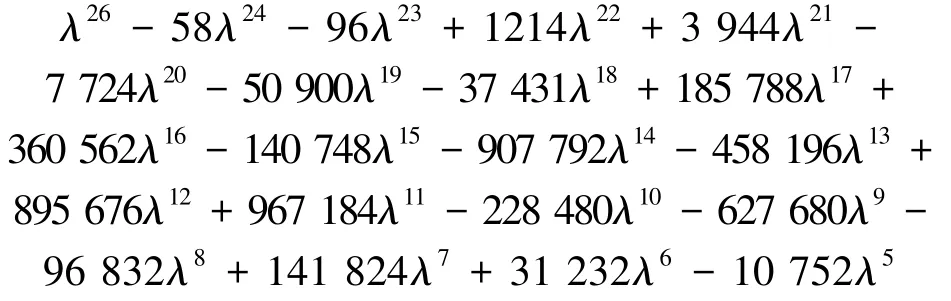
即这些广义剖分冠点图之间也是邻接同谱的。

5 结论

本文推广了剖分冠点图的定义，得到了可以冠任意图的广义剖分冠点图。可以对其他冠图作进一步的研究，尝试得到其广义定义下的图谱。巧妙地得到了无穷的邻接同谱图类，这一结论对研究化学图论有益。

［1］BROUWER A E，HAEMERS W H．Spectra of graphs［M］．New York:Springer，2012．

［2］CVETKOVIC D M，DOOB M，SACHS H．Spectra of graphs:theory and applications［M］．3rd ed．Heidelberg: Johann Ambrosius Barth，1995．

［3］CVETKOVIC D M，ROWLINSON P，SIMIC S．An introduction to the theory of graph spectra［M］．Cambridge:Cambridge University Press，2009．

［4］ZHANG Fuzhen．The schur complement and its applications［M］．US:Springer，2005．

［5］CUI Shuyu，TIAN Guixian．The spectrum and the signless Laplacian spectrum of coronae［J］．Linear algebra and its applications，2012，437（7）:1692-1703．

［6］MCLEMAN C，MCNICHOLAS E．Spectra of coronae［J］．Linear algebra and its applications，2011，435（5）:998-1007．

［7］FRUCHT R，HARARY F．On the corona of two graphs［J］．Aequationes mathematicae，1970，4（1）:264．

［8］LIU Xiaogang，LU Pengli．Spectra of subdivision-vertex and subdivision-edge neighbourhood coronae［J］．Linear algebra and its applications，2013，438（8）:3547-3559．

［9］GOPALAPILLAI I．The spectrum of neighborhood corona of graphs［J］．Kragujevac journal of mathematics，2011，35（3）:493-500．

［10］HOU Yaoping，SHIU W C．The spectrum of the edge corona of two graphs［J］．Electronic journal of linear algebra，2010，20:586-594．

［11］WANG Shilin，ZHOU Bo．The signless Laplacian spectra of the corona and edge corona of two graphs［J］．Linear and multilinear algebra，2013，61（2）:197-204．

［12］LU Pengli，MIAO Yufang．A-spectra and Q-spectra of two classes of corona graphs［J］．Journal of Donghua university:English edition，2014，31（3）:224-228．

Adjacency characteristic polynomial of generalized subdivision corona vertex graph

LU Pengli，WU Yumo
（School of Computer and Communication，Lanzhou University of Technology，Lanzhou 730050，China）

Corona graph is a composite graph obtained by graph operation from two graphs G and H．Some classes of corona graphs have been defined and studied．However，all the corona graphs in the literatures were defined as all kinds of corona graphs of graph G and H，in which graph H was n copies of grap H．By generalizing n copies of graph to arbitrary graphs in the definition of corona，a new class of corona was defined:the generalized subdivision corona vertex graph．Let S（G）be the subdivision graph of graph G by inserting a new vertex into every edge of G．Joining the ith vertex of V（G）to every vertex of Hi，the generalized subdivision corona vertex graph from graph S（G）and graph H1，H2，…，Hnwas obtained，which was denoted byWith the help of block matrix，the coronal and Schur complement，the adjacency characteristic polynomial of the generalized subdivision corona vertex graph was determined．A method to construct infinite pairs of cospectral graphs was proposed and an example was given．

composite graph；generalized subdivision corona vertex graph；adjacency characteristic polynomial；regular graphs；cospectral graphs

10．11990／jheu．201511033

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．010．html

O157．5；O157．6

A

1006-7043（2016）12-1739-04

卢鹏丽，武雨末．广义剖分冠点图的邻接特征多项式［J］．哈尔滨工程大学学报，2016，37（12）:1739-1742．

2015-11-16．

2016-09-28．

国家自然科学基金项目（11361033）．

卢鹏丽（1973-），女，教授，硕士生导师．

卢鹏丽，E-mail:lupengli88＠163．com．

LU Pengli，WU Yumo．Adjacency characteristic polynomial of generalized subdivision corona vertex graph［J］．Journal of Harbin Engineering University，2016，37（12）:1739-1742．