变幅值系数的短时Duffing振子阵列检测方法

李 楠，李秀坤，刘彩红

（1．哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001；2．哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001；3．东北电力大学信息工程学院，吉林吉林132012）

变幅值系数的短时Duffing振子阵列检测方法

李 楠1，2，3，李秀坤1，2，刘彩红1，2

（1．哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001；2．哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001；3．东北电力大学信息工程学院，吉林吉林132012）

常规Duffing振子检测方法只能确定待测弱信号的有无及幅值大小，却无法给出其在时域上的分布信息，且待测信号包络有起伏时会引起Duffing振子系统的误判。针对上述问题，本文提出可变幅值系数的短时Duffing振子阵列检测方法。应用互模糊函数推导出随机振幅包络起伏信号通过短时处理可以降低包络起伏因素对Duffing振子检测性能的影响，对信号加时间窗的短时处理可以保证窗内信号近似平稳，并可同时获得待测信号在时域上的分布信息。为克服相图判别法定性分析的不足，降低待测信号与内置策动力合成的总策动力幅值小于跃变阈值时出现的漏报误判概率，提出可变幅值系数的Poincare映射集判别方法，给出了量化统计判别结果。仿真及实测水声信号检测结果表明，在-33 dB的低信噪比背景下仍可实现信号的检测判别。

Duffing振子；短时；包络起伏；可变幅值系数；Poincare映射集；弱信号；时域分布

强噪声背景中的微弱线谱信号检测在工程应用中具有重要意义，而淹没在噪声中包络起伏的非平稳信号检测是亟待解决的问题之一。Duffing混沌振子作为一类确定性的非线性动力学系统，在微弱信号检测领域呈现出特有的优势。国外学者首先提出运用分岔理论研究Duffing振子的周期轨道及非线性能流特征，并给出了其电路系统的实现［［1-5］。国内学者则在混沌阈值的确定［6-7］、系统解的获取方法［8］及Duffing振子检测模型的改进［9-10］等方面进行了深入研究，并成功的将Duffing振子检测扩展到未知频率、未知相位的弱信号检测，取得了一定的研究成果［11-13］。

在将Duffing振子应用于水下弱信号的检测时，由于水介质声学特性和水面波度的时变性、海面和海底的声波反射及界面的不平整性而发生的散射，造成接收端水声信号是带有一定畸变的包络起伏信号。用常规Duffing振子系统检测时，难以设置统一参数实现整个包络起伏信号的精确检测。因此，本文主要致力于解决以下几个问题:1）如何准确检测包络起伏的信号，降低信号包络起伏因素造成的检测误判干扰；2）如何解决整段数据不同时间区间含有待测信号的检测问题；3）在特定内置策动力信号条件下，如何克服相图检测法定性分析的不足，并给出一种有效的量化判别方法实现任意幅值待测信号的检测。

1 常规Duffing振子系统检测方法

1．1 常规Duffing振子检测原理及存在问题

针对Holmes型Duffing方程:

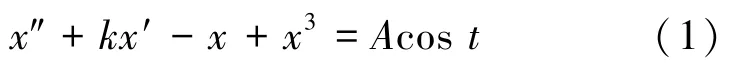
式中:k为阻尼比，-x+x3为非线性恢复力项，Acos t为系统的策动力。Duffing振子系统具有小频率参数的限制，王冠宇等［14-15］通过变量代换方法对式（1）进行处理，对时间轴做尺度变换t=ωτ，得到检测任意频率信号的Duffing方程:

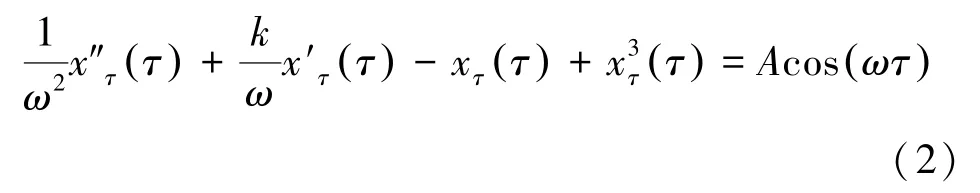
式（2）略去下标并令t=τ，整理为

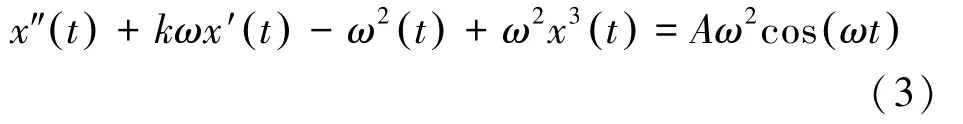
图1给出了阻尼比k=0．5时Duffing系统输出Poincare映射随着策动力幅值的变化关系。Poincare映射定义指出，在相空间中适当选取一个截面，混沌状态时，Poincare映射是相空间密集分布的点，周期状态时，Poincare映射是一个固定的点。图1策动力幅值AB段的Poincare映射为稳定值，对应同宿轨道状态；BC段的Poincare映射为密集分布的点，对应混沌状态；CD段的Poincare映射为稳定值，对应大尺度周期状态。C点处，系统处于临界混沌状态，对噪声具有很强的免疫性，策动力幅值的微小变化能激发系统由临界混沌状态跃变到大尺度周期状态。因此，可利用系统在临界值C点状态的变化实现信号的检测。

检测所用Duffing振子模型为

式中:Accos(ωt)为内置策动力信号，s(t)= Axcos(ωt)+n(t)为含有噪声的待测信号。设置内置策动力，使Duffing振子系统处于临界混沌状态，把待测数据加入到Duffing振子系统中，当系统输出状态由临界混沌状态跃变为大尺度周期状态时，可确认含有待测信号；当系统输出一直保持混沌状态，则不含待测信号。

上述检测方法是对波形稳定信号的一种全局处理方法，无法给出信号在时域上的局部分布信息。同时，对于特定内置策动力，当微弱待测信号与内置策动力合成的总策动力幅值小于跃变阈值时，出现漏报误判。现有方法不能解决包络起伏信号的检测以及整段数据中，不同时间段含有信号的检测问题，同时不能实现任意幅值待测信号的检测，而这些问题是实际工程应用中必定要面临和必须要解决的问题。因此，本文提出一种可变幅值系数的短时Duffing振子阵列检测方法解决上述问题。

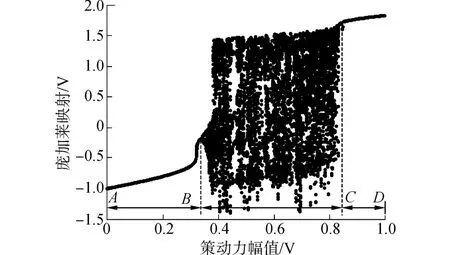
图1 系统Poincare映射与策动力幅值的关系示意图Fig．1 The diagram of the relationship between the Poincare mapping and the amplitude of the driving force

1．2 随机振幅调制包络起伏信号分析

水声信号处理时，由于水介质的不均匀性和界面的不平整性，接收端的水声信号是畸变的包络起伏信号。随机振幅调制的包络起伏信号模型:

式中:s0(t)为目标辐射信号，即待测信号；h(t)产生不平稳的调制包络；mA为随机振幅调制深度系数；x(t)是均值为0和方差为1的平稳随机过程；s(t)是测量点接收到的目标辐射信号。互模糊函数可以用来衡量接收信号相对于目标辐射信号的畸变程度，其定义如下

在调制深度系数mA的作用下，如何降低随机振幅包络起伏信号对Duffing振子跃变的影响，即如何使得期望mχ(0，0)增大、方差dχ(0，0)减小。提出可变幅值系数的短时Duffing振子阵列检测方法，选择短时窗，使得窗内信号幅值近似平稳，针对窗内平稳幅值信号，设置可以覆盖跃变阈值的可变幅值调整系数，进行Duffing振子检测。窗长越短，窗内信号幅值波动的随机性越小，经延拓处理后信号的平稳性越好，可以理解为随机振幅调制深度系数越小。此时，短时窗内信号经周期延拓后变为

式中:m′A为接收信号经短时延拓处理后振幅调制深度系数，且有m′A=αmA，0＜α＜1。此时，互模糊函数的均值和方差分别为

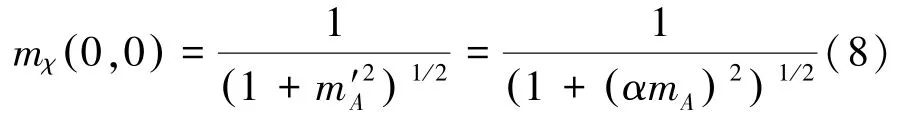
引入互模糊函数表征目标辐射信号和接收信号的匹配程度，匹配程度越大值也越大。特别地，若两者在形式上恰好匹配，均值mχ(0，0)=1，方差dχ(0，0)=0，如图2中星线所示。

可变幅值系数的短时Duffing振子阵列检测方法一个重要的参数问题是如何选取短时滑动窗的窗长。如何给出窗长选取的量化指标，窗长越短，窗内信号的幅值波动的随机性越小，信号的平稳性越好，窗长越长，窗内信号的幅值波动性越大，信号的平稳性越差。图2菱形状线和三角形状线表示包络起伏信号经不同的窗长短时处理后，得到平稳性信号的互模糊函数的均值和方差的变化曲线，三角形状线表示经较长窗处理，调制深度系数降到0．7mA时的均值和方差的变化关系曲线。菱形状线表示经较短窗处理，调制深度系数降到0．4mA时的均值和方差的变化关系曲线。图2表明，理论上窗长越短，互模糊函数的均值更接近1，方差更接近0，越能够有效抑制信号包络起伏因素对Duffing振子系统检测性能的影响，系统的检测精度越高。但是，窗长越短，对同一长度数据，短时Duffing振子阵列中所需要的Duffing振子数越多，整个系统的计算复杂度越高。因此，短时滑动窗长的选取要在系统检测精度和计算复杂度之间进行权衡。

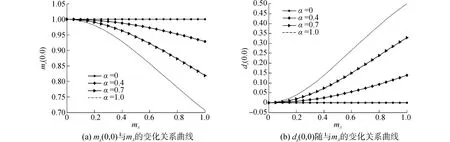
图2 模糊函数均值、方差与调制深度系数关系曲线Fig．2 Relationship curves of mean and variance of cross ambiguity function with modulation depth coefficient

针对后续周期延拓时信号相位匹配问题，窗长选取必须保证窗内含有整数倍周期的信号。因此，最短窗长即为一个信号周期，处理效果最好；最长窗长即为整个数据段，即未做任何处理。较短窗长的选取要面临的问题是信号长度过短，不能够激发Duffing振子越过过渡过程达到稳态。对短时窗内信号作周期延拓处理，以保持信号固有频率特征，也保证数据长度能够激发Duffing振子系统达到稳态。

2 一种可变幅值系数的短时Duffing振子阵列检测方法

2．1 可变幅值系数的Poincare映射集判别方法

如何给出一种有效的判别方法以检测任意幅值待测信号，降低微弱信号单次检测时，由于待测信号与内置策动力合成的总策动力幅值小于跃变阈值造成的漏报误判概率，同时克服相图判别法定性分析的不足，文中给出了一种可变幅值系数的Poincare映射集判别方法。通过调整待测信号幅值系数，依据系统状态随着策动力幅值增大所呈现出的变化规律，结合Poincare映射方法，给出待测信号在不同幅值系数下的Poincare映射集量化统计判别结果。

为便于观察系统的运动特征和变化规律，由N个一阶微分方程组成的微分方程组描述的动力系统轨迹经过的相空间中适当选取N-1维超平面，当相轨迹按照特定演化方向通过这个超平面时，截点被记录下来，第k+1次截点与第k次截点存在映射关系f:xk→xk+1，称为Poincare映射。对于只有一条周期轨道的周期吸引子，Poincare截面上只有一个点x0，这样就把周期运动状态化为映射为x0的不动点来研究。对于混沌吸引子，相轨迹极其复杂，Poincare映射是一条弧状分布的点集。动力系统决定的随时间变化的连续运动轨迹变为Poincare截面上的离散序列的映射。图3分别为大尺度周期状态和混沌状态的Poincare映射示意图及Poincare映射判别输出示意图。大尺度周期状态的Poincare映射集中在一点附近，在一个固定范围内波动；混沌状态的Poincare映射是分散于Poincare截面上弧状的离散点。利用上述特点，设置阈值，当Poincare映射持续大于阈值时，判别置1输出，否则置-1输出。

图3 Poincare映射图Fig．3 Poincare mapping

信号检测时，淹没在噪声中的微弱待测信号幅值大小是未知的。Duffing振子系统检测时，合理的内置策动力是使得待测信号能够激发系统跃变，达到检测信号的关键参数。如何针对任意幅值的待测信号进行有效检测是Duffing振子系统亟待解决的问题，提出一种可变幅值系数的Duffing振子与Poincare映射集合相结合的判别方法。使Duffing振子系统处于临界混沌状态，加入待测信号，调整待测信号幅值系数，保证待测信号和内置策动力合成的总策动力幅值范围包含跃变阈值，激发系统跃变，通过系统输出的Poincare映射集实现信号的量化统计判别。检测所用Duffing振子为

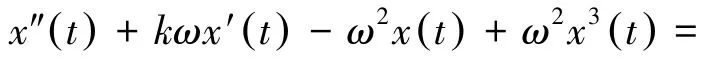
式中:Accos(ωt)是内置策动力，η是待测信号可变幅值因子，使得总策动力幅值范围覆盖跃变阈值，可以激发Duffing振子由临界混沌状态跃变到大尺度周期状态。通过调整待测信号幅值系数，若含有待测信号时，即与内置策动力同频的信号，系统输出的Poincare映射集必定由临界混沌状态跃变到大尺度周期状态，若不含待测信号，系统输出的Poincare映射集必定一直处于混沌临界状态。可变幅值系数的Poincare映射集判别方法可以降低微弱待测信号单次检测不能激发系统相态跃变造成的漏报误判概率。

图4 常规相图检测法判别结果Fig．4 Decision results of conventional phase diagram

图5 可变幅值系数的Poincare映射集判别过程Fig．5 Poincare mapping set decision process with variable amplitude coefficients

利用式（10）的检测系统，设置系统临界值为0．825。淹没在噪声中待测信号如图4（a），将待测信号加入处于临界状态的常规Duffing振子检测系统，系统输出相图如图4（b）。常规单次相图检测法并不能把淹没在噪声中的待测信号检测出来，造成漏报误判。运用可变幅值系数的Duffing振子系统，调整待测信号幅值系数η值，对待测信号实现不同幅值系数下的多次判别，结合系统输出的Poincare映射集合得到系统输出的统计判别结果。图5（a）为系统在不同幅值系数时输出的Poincare映射集合，图5（b）为Poincare映射集量化统计判别结果，随着可变幅值系数η增大，系统输出由临界混沌状态跃变到大尺度周期状态。可变幅值系数的Poincare映射集判别方法可以实现任意幅值待测信号的检测，降低常规检测法单次检测造成的漏报及误判概率。

2．2 可变幅值系数的短时Duffing振子阵列检测方法

Duffing振子系统难以设置统一的参数实现整个包络起伏信号的精确检测。实验获取的数据中，可能仅有某些时间区间含有待测信号，而剩余部分是干扰或噪声。同时，待测信号幅值是未知的，当待测信号与内置策动力合成的总策动力幅值小于系统跃变阈值时，检测系统不能发生跃变，造成检测漏报误判。针对上述问题，提出一种可变幅值系数的短时Duffing振子阵列检测方法。对待测时域信号，加滑动时间窗进行短时处理。短时处理要求窗内的信号幅值近似平稳，将滑动时间窗截取的信号送入并行Duffing振子阵列检测单元进行检测，各个检测单元中，对短时窗内的信号进行周期延拓，确保信号长度可以激发系统达到稳态，对延拓后的信号进行可变幅值系数的Duffing振子系统检测并结合Poincare映射集合方法给出量化统计判别结果。分析各个检测单元的判别结果，排除信号坏点造成的误判，给出整段数据综合判别结果。

信号短时处理要面临的问题是时间窗内信号长度不能激发Duffing振子系统进入稳态。Duffing振子系统检测信号时，是以加入待测信号后系统稳态时能否进入大尺度周期状态作为是否含有待测信号的判别依据。由于系统跃变存在过渡带，信号太短，可能待测信号不足以激发系统进入稳态，造成漏报；也可能将噪声激发出现的短暂周期状态误认为是系统进入大尺度周期状态，造成虚警。待测信号激发系统越过过渡带进入稳态所需的稳定周期数不少于15个。针对短时窗内信号太短的问题，将窗内信号进行周期延拓，使得延拓后的信号保持原信号的特征，且周期数不少于15个，保证信号能够激发Duffing振子系统越过过渡带达到稳态，降低虚警和漏报概率。

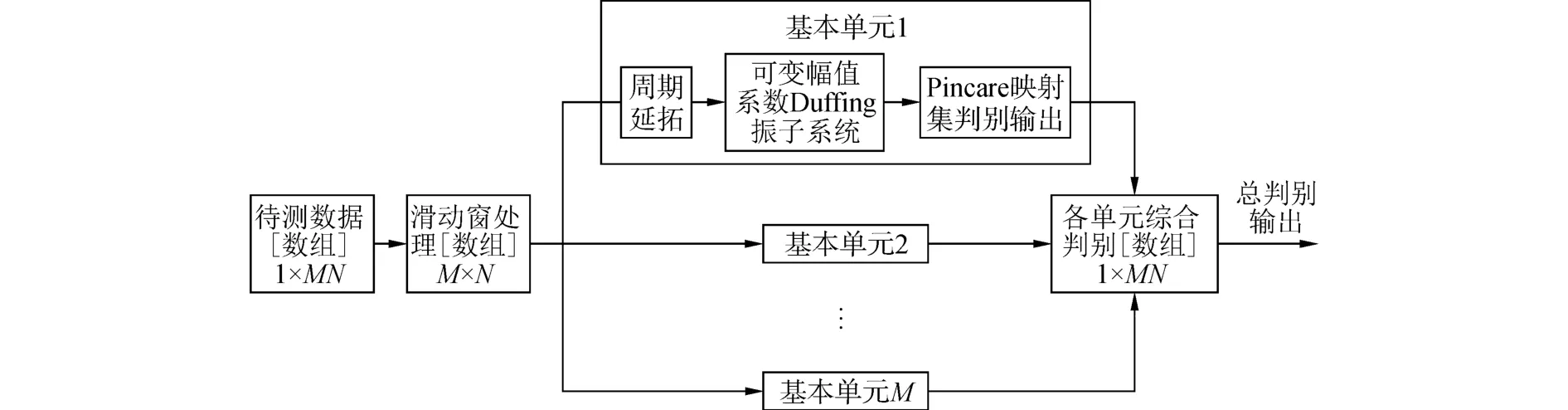
图6 可变幅值系数的短时Duffing振子阵列检测流程图Fig．6 The block diagram of the Duffing oscillator array detection with variable amplitude coefficients

可变幅值系数的短时Duffing振子阵列检测法流程图如图6所示。上述检测方法中，滑动窗函以N为窗长对待测信号分段处理，为了保证后续周期延拓处理时，延拓前后信号相位匹配，要求短时处理确保滑动窗内数据长度为待测信号整周期数，即窗长N=kfs／f0，k取正整数。通过滑动窗将1×MN的待测数据变为M×N的数据矩阵，送入并行的M个Duffing振子单元进行检测。每个检测单元中，对长度为N的数据做延拓处理后通过可变幅值系数的Duffing振子系统进行检测，给出不同幅值系数下系统输出的Poincare映射集量化统计判别结果。将各个检测单元的判别结果按照时间顺序综合分析，排除坏点信号造成的误判干扰，给出针对时间轴的判别曲线。

由上述可变幅值系数的短时Duffing振子阵列检测方法的原理和方法分析，结合图6的检测原理框图，给出针对包络起伏微弱信号的检测步骤:

1）设置各个基本检测单元中Duffing振子参数可变幅值系数η调整范围；

2）根据待检测信号包络起伏情况和检测精度要求设置短时窗，通过滑动窗函数F( s( n)，N)对待测信号s( n)滑动分段处理，数据长度是待测信号的整周期数，确保窗内信号近似平稳，将窗函数截取的分段信号送入并行Duffing振子阵列检测单元进行处理；

3）对每个检测单元中的数据周期延拓，确保信号长度激发Duffing振子系统达到稳态，将延拓处理后的数据通过可变幅值系数的Duffing振子系统（10）进行检测，获取不同幅值系数下系统输出的Poincare映射集合，给出量化统计判别结果；

4）综合各个检测单元判别结果，排除信号坏点造成的误判干扰，绘出信号针对时间轴的整体判别曲线。

3 数据处理结果

下面给出一个淹没在噪声中的包络起伏的CW脉冲周期信号的检测和一组实测水声信号的检测结果，分别给出常规检测方法和可变幅值系数的短时Duffing振子阵列检测法两种方法的判别结果。

分析1:针对常规Duffing振子检测系统（4）和可变幅值系数的Duffing振子检测系统（10），临界值设为0．825，阻尼比设为0．5，系统跃变阈值为0．826。s1(t)为一个包络起伏CW脉冲周期信号，s2(t)是淹没在噪声中的s1(t)信号。待测信号幅值为0．001 V，内置策动力频率取值与待测信号频率相同。加入功率为0．001 W的高斯白噪声，信噪比为特别地，详细给出短时窗在含有信号段和不含信号段滑动截取整周期信号1、2、3、4的检测判别结果。图7分别是未加噪声的包络起伏信号s1(t)和淹没在噪声中的包络起伏信号s2(t)以及获取待处理信号的位置。受信号包络起伏因数的影响，截取的信号2幅值小于待测信号幅值。对信号1～4进行周期延拓，确保信号长度激发Duffing振子系统越过过渡过程达到稳态，将延拓处理后的信号通过Duffing振子检测系统进行检测。图8～11分别是信号1～4通过常规Duffing振子检测系统和可变幅值系数的Duffing振子检测系统的判别结果。常规Duffing振子检测结果受到信号包络起伏因素的影响，信号1、3相图发生跃变，检测到信号，信号2未发生跃变，出现检测漏报；可变幅值系数的Duffing振子检测系统检测时，信号1～3的Poincare映射集都发生混沌状态到大尺度周期状态的跃变。

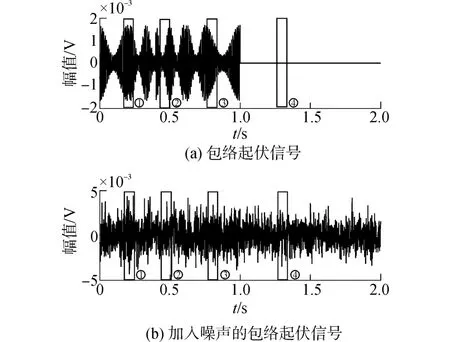
图7 待测包络起伏信号及获取待处理信号位置Fig．7 Envelope fluctuation signal and the positions of the signal to be processed

图8 信号1常规Duffing振子与改进Duffing振子系统检测结果对比Fig．8 Comparison of the detection results between the normal Duffing oscillator and improved Duffing oscillator for signal 1

图9 信号2常规Duffing振子与改进Duffing振子系统检测结果对比Fig．9 Comparison of the detection results between the normal Duffing oscillator and improved Duffing oscillator for signal 2

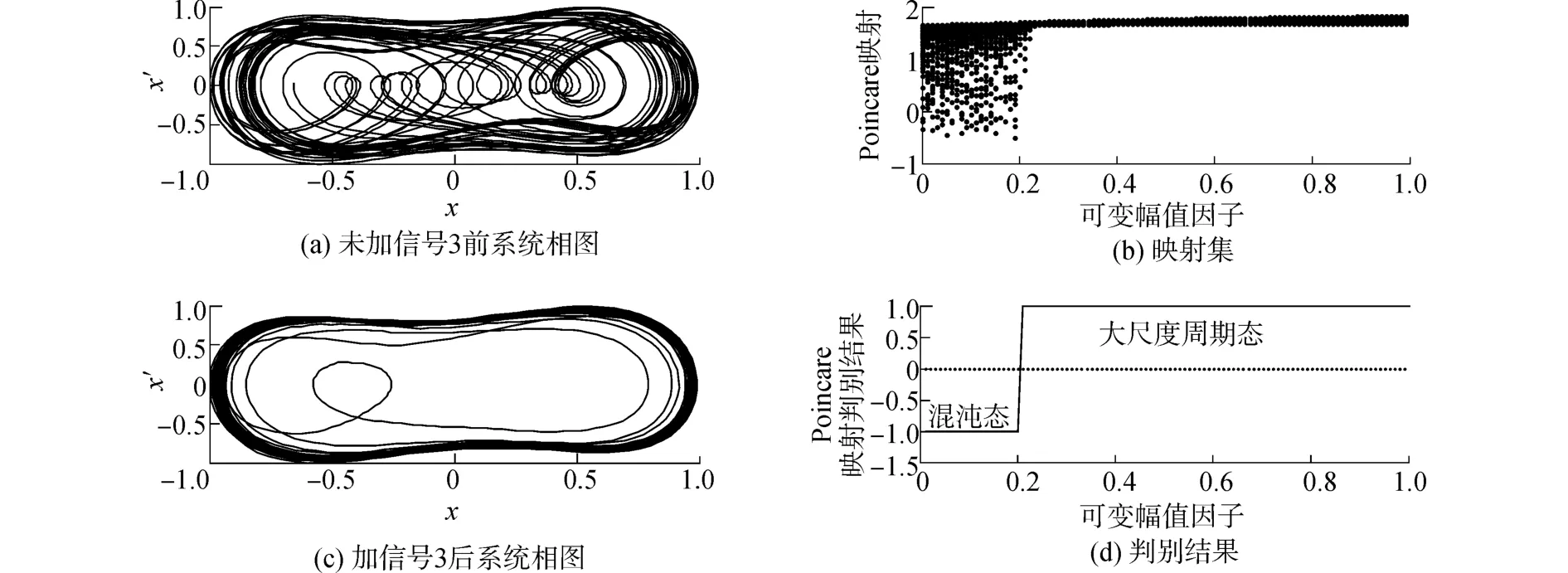
图10 信号3常规Duffing振子与改进Duffing振子系统检测结果对比Fig．10 Comparison of the detection results between the normal Duffing oscillator and improved Duffing oscillator for signal 3

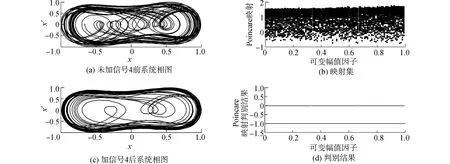
图11 信号4常规Duffing振子与改进Duffing振子系统检测结果对比Fig．11 Comparison of the detection results between the normal Duffing oscillator and improved Duffing oscillator for signal 4

分析2:给出一组含有CW脉冲信号的实测水声信号的处理结果。内置策动力临界值设为0．825，内置策动力频率取值与待测信号频率相同，为求得较高精度结果，短时窗长选取5个信号周期并延拓至30个信号周期再通过常规Duffingz振子检测系统和可变幅值系数的Duffing振子系统进行检测。图12和图13分别是常规检测方法和可变幅值系数的短时Duffing振子阵列检测方法的判别结果。

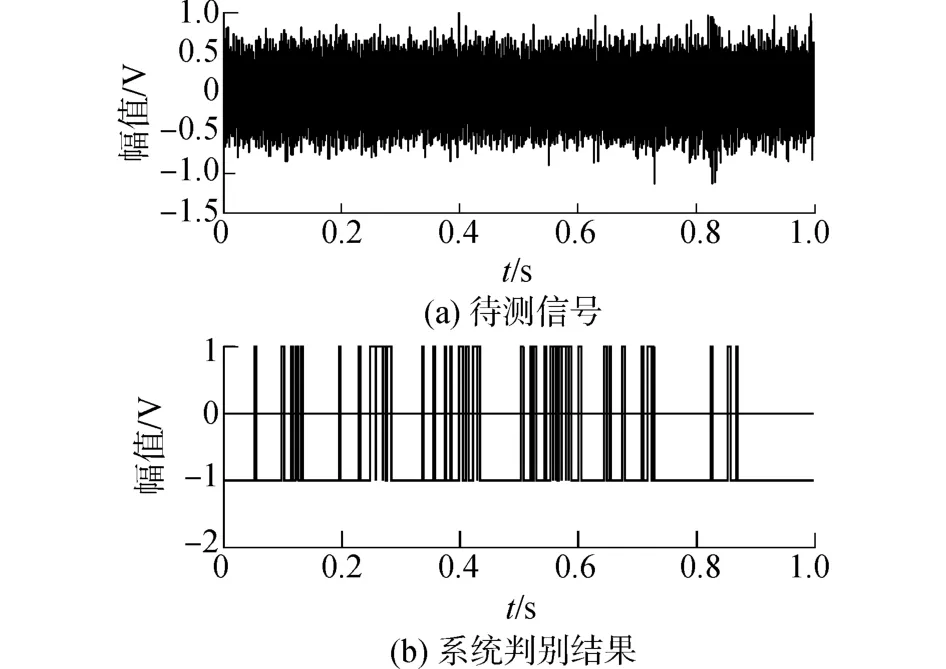
图12 常规Duffing振子方法检测结果Fig．12 Detection result of conventional Duffing oscillator method

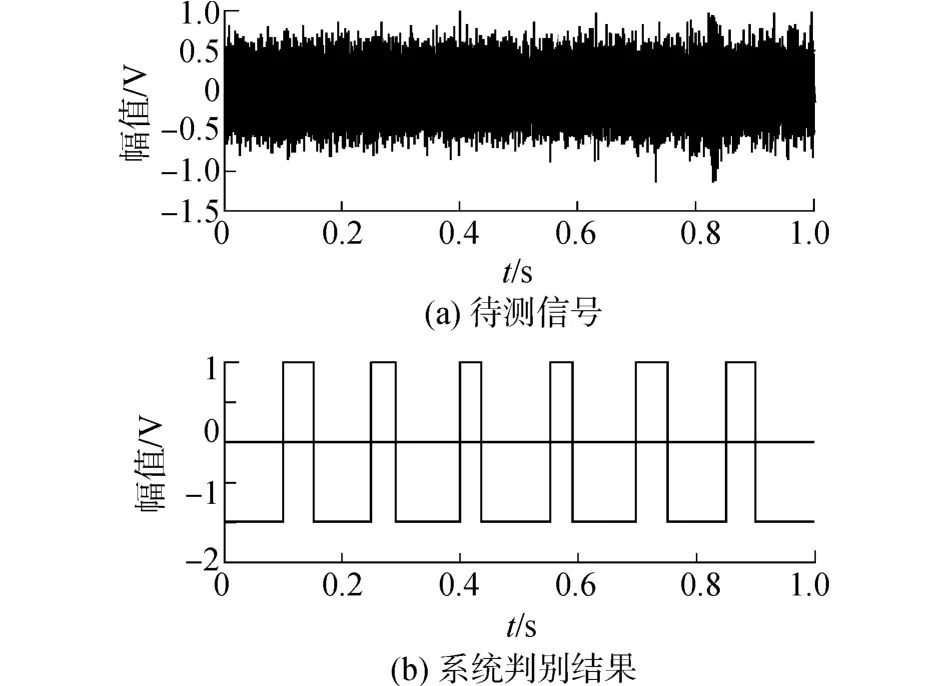
图13 可变幅值系数的短时Duffing振子阵列方法检测结果Fig．13 Detection result of short-time Duffing oscillator array method with variable amplitude coefficients

实测水声信号判别结果表明，对于分布于不同时间区间带有一定畸变的包络起伏的待测信号，常规Duffing振子检测方法不能把各个时间区间的待测信号准确检测出来。可变幅值系数的短时Duffing振子阵列检测法能够降低信号包络起伏因数的影响，检测出淹没在噪声中受到包络起伏因数影响的不同时间区间内不同幅值的待测信号。

4 结论

本文针对Duffing振子系统信号检测过程中，待测信号包络起伏难以设置统一系统参数进行精确检测以及现有检测方法无法检测任意幅值待测信号的问题，进行了推导与实验验证，得到以下结论:

1）常规Duffing振子检测方法仅限于波形平稳的信号检测，针对待测包络起伏信号以及不同时间段分布信号的检测问题，构造可变幅值系数的短时Duffing振子阵列，通过短时及延拓处理，可以降低信号包络起伏因素的影响，调整信号幅值系数结合Poincare映射集给出量化统计判别结果，实现包络起伏信号和不同时间区间信号分布的准确判别；

2）为降低待测信号与内置策动力合成的总策动力幅值小于跃变阈值时造成的漏报及误判概率，构造可变幅值系数的Poincare映射集判别方法，调整幅值系数，保证待测信号和内置策动力合成的总策动力幅值范围包含跃变阈值，激发系统跃变，通过不同幅值系数的Poincare映射集实现信号的量化统计判别。可变幅值系数的Poincare映射集判别方法克服相图检测法定性分析的不足，降低常规检测法出现的漏报误判概率，实现任意幅值待测信号的检测。

［1］GUCKENHEIMER J，HOLMES P J．Nonlinear oscillations，dynamical systems，and bifurcations of vector fields［M］．New York:Springer-Verlag，1983:82-92．

［2］BONATTO C，GALLAS J A C，UEDA Y．Chaotic phase similarities and recurrences in a damped-driven Duffing oscillator［J］．Physical review e，2008，77（2）:026217．

［3］SABARATHINAM S，THAMILMARAN K，BORKOWSKI L，et al．Transient chaos in two coupled，dissipatively perturbed Hamiltonian Duffing oscillators［J］．Communications in nonlinear science and numerical simulation，2013，18（11）:3098-3107．

［4］YANG J，XIONG Y P，XING J T．Nonlinear power flow analysis of the Duffing oscillator［J］．Mechanical systems and signal processing，2014，45（2）:563-578．

［5］ROSTAMI M，HAERI M．Undamped oscillations in fractional-order Duffing oscillator［J］．Signal processing，2015，107:361-367．

［6］李月，石要武，马海涛，等．湮没在色噪声背景下微弱方波信号的混沌检测方法［J］．电子学报，2004，32（1）: 87-90． LI Yue，SHI Yaowu，MA Haitao，et al．Chaotic detection method for weak square wave signal submerged in colored noise［J］．Acta electronica sinica，2004，32（1）:87-90．

［7］SHI Huichao，FAN Shangchun，XING Weiwei，et al．Study of weak vibrating signal detection based on chaotic oscillator in MEMS resonant beam sensor［J］．Mechanical systems and signal processing，2015，50-51:535-547．

［8］王坤，关新平，丁喜峰，等．Duffing振子系统周期解的唯一性与精确周期信号的获取方法［J］．物理学报，2010，59（10）:6859-6863．WANG Kun，GUAN Xinping，DING Xifeng，et al．Acquisition method of precise periodic signal and uniqueness of periodic solutions of Duffing oscillator system［J］．Acta physica sinica，2010，59（10）:6859-6863．

［9］DENG Xiaoying，LIU Haibo，LONG Teng．A new complex Duffing oscillator used in complex signal detection［J］．Chinese science bulletin，2012，57（17）:2185-2191．

［10］JIANG Haibo，ZHANG Liping，YU Jianjiang．Complex dynamics analysis of impulsively coupled Duffing oscillators with ring structure［J］．Chinese physics b，2015，24（2）: 020502．

［11］丛超，李秀坤，宋扬．一种基于新型间歇混沌振子的舰船线谱检测方法［J］．物理学报，2014，63（6）:064301．CONG Cao，LI Xiukun，SONG Yang．A method of detecting line spectrum of ship-radiated noise using a new intermittent chaotic oscillator［J］．Acta physica sinica，2014，63（6）:064301．

［12］CHANG Yuan，HAO Yi，LI Chunwen．Phase dependent and independent frequency identification of weak signals based on Duffing oscillator via particle swarm optimization［J］．Circuits，systems，and signal processing，2014，33（1）:223-239．

［13］牛德智，陈长兴，班斐，等．Duffing振子微弱信号检测盲区消除及检测统计量构造［J］．物理学报，2015，64（6）:060503．NIU Dezhi，CHEN Changxing，BAN Fei，et al．Blind angle elimination method in weak signal detection with Duffing oscillator and construction of detection statistics［J］．Acta physica sinica，2015，64（6）:060503．

［14］王冠宇，陶国良，陈行，等．混沌振子在强噪声背景信号检测中的应用［J］．仪器仪表学报，1997，18（2）: 209-212．WANG Guanyu，TAO Guoliang，CHEN Xing，et al．The application of chaotic oscillator to signal detection in strong background noise［J］．Chinese journal of scientific instrument，1997，18（2）:209-212．WANG Guanyu，CHEN Dajun，LIN Jianya，et al．The application of chaotic oscillators to weak signal detection［J］．IEEE transactions on industrial electronics，1999，46（2）:440-444．

Detection method of a short-time Duffing oscillator array with variable amplitude coefficients

LI Nan1，2，3，LI Xiukun1，2，LIU Caihong1，2
（1．Acoustic Science and Technology Laboratory，Harbin Engineering University，Harbin 150001，China；2．College of Underwater A-coustic Engineering，Harbin Engineering University，Harbin 150001，China；3．College of Information Engineering，Northeast Dianli University，Jilin 132012，China）

The conventional detection method for a Duffing oscillator can determine if a weak signal exists and can determine the amplitude value of that signal but gives no distribution information in the time domain．wrongful judgments of the system are caused by the envelope fluctuation of this signal．A detection method of a short-time Duffing oscillator array detection method of a with variable amplitude coefficients is proposed for the above problems．By using a cross-ambiguity function，we observed that the influence of the envelope fluctuation factors on the detection performance of the Duffing oscillator can be reduced by short-time processing．Adding a short-time window ensures that the signal in the window is approximately stable．Simultaneously，distribution information on the measured signal in the time-domain is obtained by window analysis．To overcome the shortcomings of the phase diagram discrimination method in quantitative analysis and to reduce the error probability caused by the amplitude of the total driving force being less than the jump threshold，a Poincare mapping set identification method with variable amplitude coefficients is proposed and quantitative statistical results are given．Simulation and experimental results show that the signal can be detected even when the signal to noise ratio is-33 dB．

Duffing oscillator；short-time processing；envelope fluctuation；variable amplitude coefficient；Poincare mapping set；weak signal；distribution in time-domain

10．11990／jheu．201511062

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．002．html

TN911．7

A

1006-7043（2016）12-1645-08

李楠，李秀坤，刘彩红．变幅值系数的短时Duffing振子阵列检测方法［J］．哈尔滨工程大学学报，2016，37（12）:1645-1652．

2015-11-25．

2016-09-28．

国家自然科学基金项目（51279033）；黑龙江省自然科学基金项目（F201346）．

李楠（1973-），女，副教授，博士研究生；

李秀坤（1962-），女，教授，博士生导师．

李秀坤，E-mail:lixiukun＠hrbeu．edu．cn．

LI Nan，LI Xiukun，LIU Caihong．Detection method of a short-time Duffing oscillator array with variable amplitude coefficients［J］．Journal of Harbin Engineering University，2016，37（12）:1645-1652．