把握灵动资源 打造动态课堂
楼惠英
摘要:《全日制义务教育数学课程标准(实验稿)》指出:“数学是预设与生成、封闭与开放的矛盾统一体。”数学教学既需要预设,也需要生成,预设是手段,生成是目的。本文从珍视“意外”,会有不曾预约的精彩;善待“节外生枝”,碰撞出智慧的火花;把握“变化”,促成美丽的生成;利用“错误”的资源,演绎别样精彩四个方面对动态生成进行研究。
关键词:课前预设;课堂教学;课堂生成
布卢姆曾说“人们无法预料到教学所生成的成果的全部范围”。教学的精彩生成,离不开教师的精心设计,同时更需要老师在课堂中及时捕捉教学中的生成资源,让它成为教学的契机,使我们的课堂逐渐充盈着智慧、灵性和由此而萌发的勃勃生机。
如何把握课堂中的灵动资源,打造动态课堂呢?本人从以下几个方面进行了研究。
一、珍视“意外”,会有不曾预约的精彩
随着学生课堂主体性,自主性的增强,学生质疑、反驳、争论的机会已大大增多。教师应该学会倾听,并在倾听过程中及时发现他们困惑的焦点、理解的偏差、观点的创意、批评的价值。针对其中有价值的“意外”合理打乱教学节奏,演绎不曾愉悦的课堂精彩,完全可以开发有效的教学资源。然而,教师要及时地根据课堂上获得的信息,善于抓住契机,充分利用意外事件中具有一定教学价值的动态资源,及时调整教学方案,不断激发学生的创造才能。
二、善待“节外生枝”,碰撞出智慧的火花
在动态生成的课堂上,常会出现令人感到意外而惊喜的回答。面对教学过程中的“节外生枝”,我们不能听之任之,放任自流,而要给予密切地关注与亲切地呵护,让“有益”的课堂生成资源开出灿烂的花朵。
三、把握“变化”,促成美丽的生成
课堂教学具有较强的现场性,学习的状态、条件随时会发生变化,当条件发生变化的时候,目标需要开放地纳入弹性灵活的成分,接纳始料未及的信息。随着课堂的推进,预设目标会显出它的不合理、不完善,教学就要合理地删补、升降预设目标,从而即时生成目标。
四、利用错误资源,演绎别样精彩
课堂教学是一个生成性的动态过程,有着一些我们无法预见的教学因素和教学情景,其实,数学课堂中的“精彩”很多时候都是出其不意的,我们备课时很难预料到,这就需要我们老师顺着学生的思路,从容地处理每个环节,充分展示学生思考、探索、交流的过程,使数学课堂中的“错误”转变成精彩的“催化剂。”
案例4:《平行四边形的面积》教学
(1)导入揭题
(出示 )在日常生活中,经常要用到我们让你去计算平行四边形的面积。
(2)制造冲突
请同学们利用作业纸上的平行四边形测量、计算并探究平行四边形面积的计算方法(测量时保留整厘米)。学生独立测量他认为自己所需的各条长度并进行面积的计算后集体交流、反馈。
你算得的平行四边形面积是多少?
学生回答:28平方厘米、14平方厘米、35平方厘米、24平方厘米……
汇报并统计人数。
(3)动态生成
谁来说说你的结果是怎么来的?
生1:我认为面积应该是35平方厘米,因为底边是7厘米,斜边是5厘米,根据长方形的面积等于长乘宽而推想得到,5×7=35平方厘米
生2:我认为面积应该是28平方厘米,因为底边是7厘米,底边上的高是4厘米,7×4=28平方厘米。
生3:我的24平方厘米用(7+5)×2得到。
验证得出生3说的是平行四边形的周长,而不是面积。
生4:我是14平方厘米,7+7=14平方厘米。——算得是两底边的总长。
在35平方厘米、28平方厘米有没有正确的答案在里面?(赞成生1的占大多数)
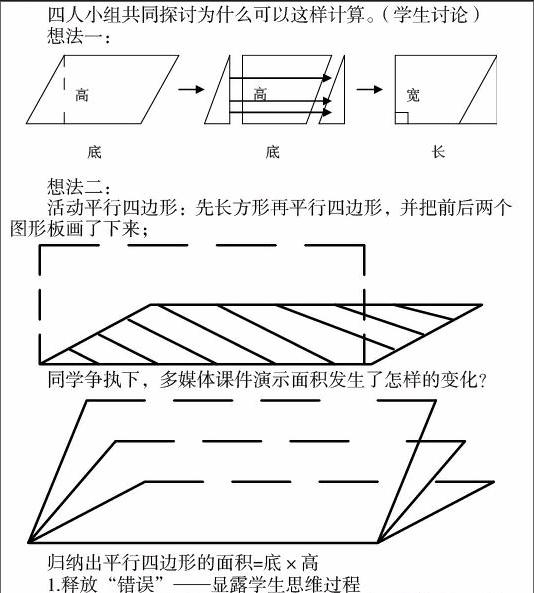
四人小组共同探讨为什么可以这样计算。(学生讨论)
想法一:
想法二:
活动平行四边形:先长方形再平行四边形,并把前后两个图形板画了下来;
同学争执下,多媒体课件演示面积发生了怎样的变化?
归纳出平行四边形的面积=底×高
1.释放“错误”——显露学生思维过程
在《平行四边形的面积》教学中,让学生计算并探究平行四边形面积的计算方法。结果,许多学生认为平行四边形面积应该是35平方厘米,根据长方形的面积等于长乘宽推想得到。针对错误,让学生四人小组共同探讨“平行四边形为什么是28平方厘米”从而推倒出平行四边形面积公式。通过操作,学生自然而然明白了平行四边形的面积公式。
2.关注“错误”——引导学生辨别理解
当学生在课堂上出错时,教师要充分发挥学生之间的互补功能,想办法纠正错误。但这件事没必要早早地向学生透露解决问题的统一方法,而是提供学生探索的空间,让学生合作交流,各抒己见,主动寻求解决问题的方法。
总之,课堂上的教学活动是师生互动的建构、共同成长的过程。“动态生成”是其鲜明的特征。因此在教学过程中,反思自己的教学行为,及时调整组织教学,让教学过程沿着最佳的轨道运行。这样我们的学生的个性才能得到张扬,思维的活化才能得到绽放,我们凝固的课堂场景才能变成一副副鲜活的、生动的画面,流淌出生命的活力。

