函数对称性的类比推理与数理证明

◇ 江苏 杨欢涛

函数对称性的类比推理与数理证明

◇ 江苏 杨欢涛

函数的基本性质在高中课程标准中是难点也是重点,同时在高考要求上属于C级,所以我们在高考题或调研考试的中档题中经常见到如“函数f(x)关于x＝a对称”或“f(a＋x0)＝f(a－x0)”的题设条件.研究高中数学中函数的性质往往绕不开函数的对称性,而事实上高中数学中许多函数不仅具有优美的对称图象,而且还具有优美的对称表达式.众所周知,对称关系存在轴对称和中心对称之分,本文尝试从数学推理和理论证明的角度来讨论函数对称性.

1 轴对称函数对称性类比与论证

学生最熟悉的轴对称函数非偶函数莫属.偶函数关于y轴对称,因此有f(x)＝f(－x).关于y轴对称,其实质是关于x＝0对称.

1)类比推理.

如图1,函数y＝f(x)关于直线x＝a(a＞0)对称,以“偶函数关于x＝0对称,则f(x)＝f(－x)”为基础,不难推理得出结论:“若函数y＝f(x)关于直线x＝a对称,则f(a＋x)＝f(a－x).”其类比推理过程如下:关于直线x＝a对称的函数f(x),可看成由关于x＝0对称的函数平移得来,原图象上一组对称点P和P′,平移后在新图象上对应的坐标可分别记为(a＋x,f(a＋x))和(a－x,f(a－x)).因为这是一组对称点的水平移动,纵坐标大小不变,显然存在f(a＋x)＝f(a－x).反之,上述命题的逆命题也成立,即:“若f(a＋x)＝f(a－x),则若函数y＝f(x)关于直线x＝a对称.”当然这仅仅是逻辑上推演,要证明命题“若函数y＝f(x)关于直线x＝a对称,则f(a＋x)＝f(a－x)”,必须有充分的理论证明.

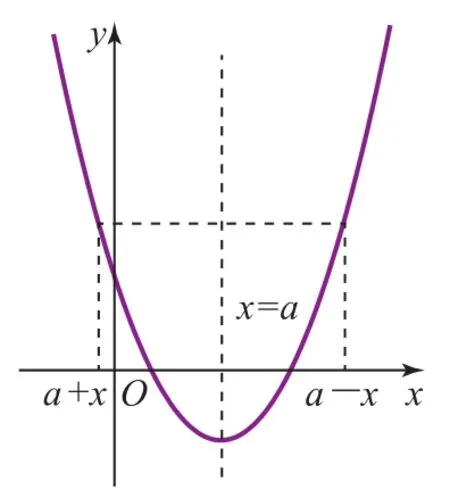
图1

2)理论证明.

证明命题“若函数y＝f(x)关于直线x＝a对称,则f(a＋x)＝f(a－x)”,需要从充分性和必要性2方面进行说明.充分性证明:不妨设函数上任意点P坐标为(a＋x,f(a＋x)),由轴对称的性质易知点P关于直线x＝a对称点P′也在函数f(x)的图象上,其坐标满足函数y＝f(x)的表达式.根据中点坐标公式易得xP′＝a－x,所以点P′的纵坐标yP′＝f(ax).又因为点P与点P′关于直线x＝a对称,所以f(a＋x)＝f(a－x).必要性证明:在函数y＝f(x)的图象上任取一点P记其坐标为(a＋x,f(a＋x)),若点P关于x＝a的对称点也在函数图象上,则函数y＝f(x)关于直线x＝a对称.易知P关于直线x＝a对称点的横坐标为xP′＝a－x,根据对称关系显然P′的纵坐标可记为yP′＝f(a＋x).又因f(a＋x)＝f(a－x),所以点P′的坐标可记为(a－x,f(ax)),所以P′的坐标满足函数y＝f(x)的关系式,即点P′也在函数图象上,所以必要性得证.

3)补充证明.

结论1:若函数y＝f(x)关于直线x＝a对称,则f(x)＝f(2a－x).不妨令上述结论中的a＋x＝t,移项后可得x＝t－a,以t－a替换x,显然a－x＝2at,因此就存在f(t)＝f(2a－t),也即f(x)＝f(2ax).不妨设结论1中的2a＝b,则结论1的形式就可变为结论2:若函数y＝f(x)关于直线x＝对称,则f(x)＝f(b－x).借助上述理论证明过程,不难证明结论3:若函数y＝f(x)关于直线对称,则f(a＋x)＝f(b－x).

2 点对称函数对称性的分析与证明

关于点(中心)对称函数的对称表达式又呈现出什么样的形式呢?这可从奇函数对称性表达式的类比中窥得一斑,并且通过理论的证明来印证.

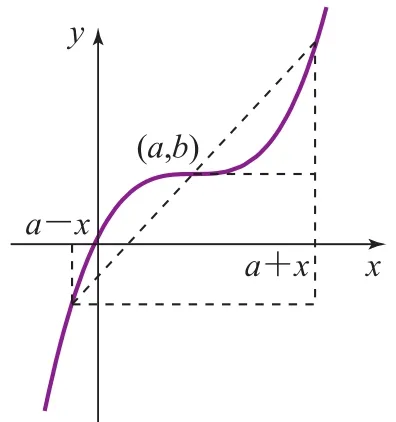
图2

1)类比推理.

众所周知,奇函数关于原点对称,其对称表达式为f(x)＋f(－x)＝0,以此为基础,不难类比出命题:若函数y＝f(x)关于点(a,b)对称,则f(a＋x)＋f(a－x)＝2b.如图2不妨假设a＞0、b＞0,则函数y＝f(x)可视为原奇函数向右平移a个单位,再向上平移b个单位形成,在此过程中原图象上任意一组对称点P和P′,在平移后其对应坐标分别可记为(a＋x,f(a＋x))和(a－x,f(a－x)),根据中心对称的特性(对称点连线经过对称点且被对称点平分)并结合中点坐标公式可得f(a＋x)＋f(a－x)＝2b.同样,其逆命题也成立,即:“若f(a＋x)＋f(a－x)＝2b,则y＝f(x)关于点(a,b)对称.”

2)理论证明.

充分性证明:在y＝f(x)上任取一点P(a＋x,f(a＋x)),根据中心对称的性质,易知点P关于点(a,b)中心对称点P′也在f(x)的图象上,其坐标应满足函数y＝f(x)的表达式.根据中点横坐标公式易得xP′＝a－x,所以点P′的纵坐标yP′＝f(a－x),利用中点纵坐标公式可得f(a＋x)＋f(a－x)＝2b.

必要性证明:在函数y＝f(x)的图象上任取一点P记其坐标为(a＋x,f(a＋x)),若点P关于点(a,b)中心对称点P′也在函数f(x)的图象上则函数y＝f(x)关于点(a,b)对称.易知点P关于点(a,b)中心对称点的横坐标为xP′＝a－x,根据对称关系显然P′的纵坐标可记为yP′＝2b－f(a＋x).又因为f(a＋x)＋f(a－x)＝2b,所以点P′的坐标可记为(a－x,f(a－x)),所以P′的坐标满足函数y＝f(x)的关系式,即点P′也在函数图象上,所以必要性得证.

3)补充说明.

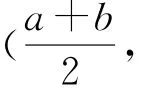
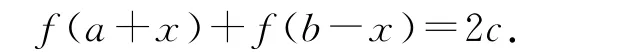
反思上述函数对称性的逻辑推理与数理证明过程,不难发现这种对称性的结论与奇偶函数对称性结论存在极大的相关性.因为偶函数关于y轴对称,奇函数关于原点对称,所以只需要研究其在区间(－∞,0)上的性质,就可知道函数在对应区间(0,＋∞)的图象和性质.而上述对称性结论是研究函数在区间(－∞,a)上的图象和性质,就可知道函数在其对称区间(a,＋∞)上的图象和性质.所以上述对称思想研究函数的图象和性质可以看成奇、偶函数对称性结论的推广.

(作者单位:江苏省苏州市第一中学)