把握“三看”绽放“三景”——谈三角变换的复习

◇ 云南 张红林

把握“三看”绽放“三景”
——谈三角变换的复习

◇ 云南 张红林

尽管新课标对三角恒等变形的要求有所下降,但三角恒等变换仍是高考考查的重点,化简、求值与证明构成三角恒等变换的三道亮丽的风景线,解决此类问题必须掌握三角恒等变换的一些常规方法和技巧,把握三看:看角、看名称、看结构.其中角的变换是三角变换的核心与灵魂,注意观察已知角与所求角之间的和、差、倍的关系,注意题中角与特殊角的关系,正确选择解题的突破口.

1 三角函数式的化简

解析

整体观察可将2α－β变换为α＋(α－β),从而迈出解题的关键一步.

点评

在三角化简、求值与证明中,往往会出现较多相异的角,这时可根据角与角之间的和、差、倍、半、互补、互余等关系,运用角的变换,沟通条件与结论中角的差异,使问题获解.常用角的变换有:

解析

观察结构特点,利用二倍角公式,原式可化为

点评

2 三角函数的求值

解析

变倍角为单角是明显的解题方向.

点评

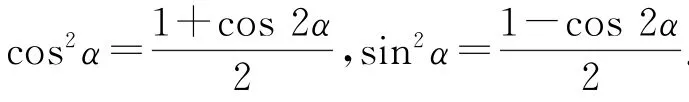
3 三角函数的证明

点评

证明三角恒等式的实质是消除等式两边的差异,有目的地化繁为简、左右归一或变更论证,常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变换法等.当然本题也可以用切化弦.

(作者单位:云南省红河州泸西县泸源普通高级中学)