分类例说双变量问题的求解策略
吴旭红
(江苏省常熟市中学,215500)
分类例说双变量问题的求解策略
吴旭红
(江苏省常熟市中学,215500)
一、单一函数类
1.恒成立问题
例1 已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时f(x)取得极值-2.
(1)求f(x)的单调区间和极大值;
(2)证明对任意x1,x2∈[-1,1],不等式|f(x1)-f(x2)|<4恒成立.
分析 本题是同一函数的最值问题,只需求出函数f(x)在[-1,1]上的最值(或范围),再由|f(x)max-f(x)min|<4着手即可.
2.零点问题
例2 已知二次函数f(x)=ax2+bx+c.
(1)若a>b>c,且f(1)=0,试证明f(x)必有两个零点;

分析 本题第(2)问使用零点存在定理,用f(x1)·f(x2)与0的大小比较,学生往往无从下手,联想不到零点存在定理.
3.斜率等式型
例3 设函数f(x)=ax+sin x+cos x,若函数f(x)图象上存在不同的两点A,B,使得曲线y=f(x)在A,B处的切线互相垂直,则实数a的取值范围是______.

函数f(x)在不同的两点A,B处的斜率

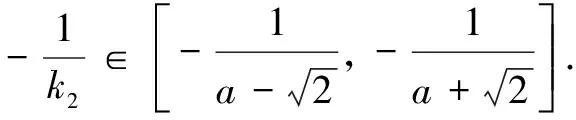
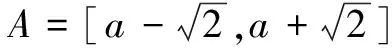




∴-1≤a≤1.

二、两个函数类
1.常规任意存在问题
常规任意存在问题,相对简单.不等式型基本规则如下:假如函数f(x),g(x)分别在其定义域M,N内最值存在,则
∀x1∈M,x2∈N,都有f(x1)≥g(x2),可得f(x)min≥g(x)max;
∀x1∈M,∃x2∈N,使f(x1)≥g(x2),可得f(x)min≥g(x)min;
∃x1∈M,∀x2∈N,使f(x1)≥g(x2),即f(x)max≥g(x)max;
∃x1∈M,x2∈N,使f(x1)≥g(x2),即f(x)max≥g(x)min.
此类问题学生掌握较好,弄清模式,在最值取不到或者不等号为“>”、“ <”时注意区间的端点是否取到,就可以解决问题.等式型问题理解上相对困难,需要理解存在为大(子集)原则.如:∀x1∈M,∃x2∈N,使f(x1)=g(x2)的解题策略为:若f(x)在M上值域为A,g(x)在N上值域为B,则A⊆B.类似于上述斜率等式型.
2.构造型任意性问题
(1)当a=1 时,求函数 f(x) 的最小值;
(2)当a<0 时,讨论函数 f(x) 的单调性;

分析 本题解决问题的关键是构造函数.对于(3),不妨设0
初接触这类问题时,学生往往用导函数f′(x)>a处理,原因是他们对导函数和平均变化率的关系混淆,需要引导学生进行区别,学会等价转化.
3.构造型存在性问题
(1)求f(x)的单调区间;
(2)令g(x)=ax2-2ln x,则g(x)=1时有两个不同的根,求a的取值范围;
(3)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)-f(x2)|≥k|ln x1-ln x2|成立,求k的取值范围.
解 (1)(2)略.
(3)不妨设x1>x2>1,由(1)知x∈(1,+∞)时,f(x)单调递减.
|f(x1)-f(x2)|≥k|ln x1-ln x2|
等价于f(x2)-f(x1)≥k(ln x1-ln x2),
即 f(x2)+kln x2≥f(x1)+kln x1,
也即存在x1,x2∈(1,+∞)且x1≠x2,使f(x2)+kln x2≥f(x1)+kln x1成立.


本题的关键是构造函数.但由于不等号为“≥”,与例4不同,本题为不等式有解问题,需要注意不等号,区别于恒成立问题.亦可以先求反面,转化为恒成立问题.
三、综合应用类
1.与对数函数相关
例6 已知直线x-y-1=0为曲线f(x)=logax+b在点(1,f(1))处的一条切线.
(1)求a,b的值;

解 (1)略. a=e, b=0.
(2)先求出k1,k2(用x1,x2表示),探寻k1,k2两者的关系,然后结合基本不等式求解.
f(x)=ln x,




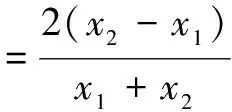
以下有两种处理方法:
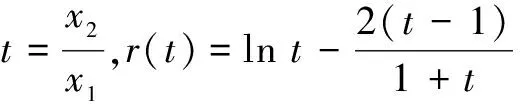
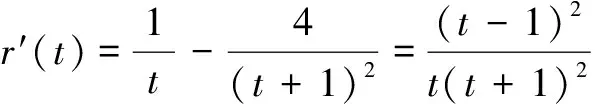
∵t>1时,r′(t)>0,∴r(t)在[1,+∞)上单调递增,∴r(t)>r(1)=0,∴k2>k1.



2.与指数函数相关

解 (1)a>e2(过程略).
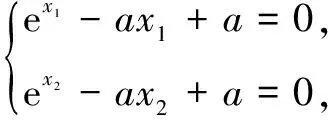
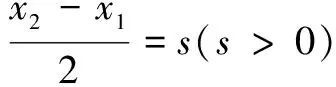
设g(s)=2s-(es-e-s),则g′(s)=2-(es+e-s)<0,∴g(s)是单调减函数,则有
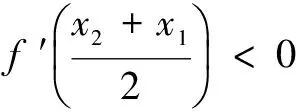
又f ′(x)=ex-a是单调增函数,且

(3)依题意,有exi-axi+a=0,则a(xi-1)=exi>0,∴xi>1(i=1,2)),且

由直角三角形斜边的中线性质,可知
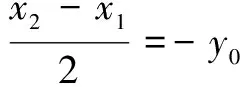



=0.


∴(a-1)(t-1)=2.
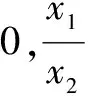
解析几何中的曲线上的两点问题也比较多,本质是点的双重身份,即既在这个曲线上,又在那条曲线(直线)上,亦即方程组的根,处理方法往往联立方程,或者用点差思想,本文不再赘述.
总之,双变量问题首先要让学生通过练习熟悉题型,在此基础上学习解题策略,再通过思考,归纳解决问题的方法:以单调性为背景,集合思想为原则,构造函数为桥梁,函数定义域为根本,等价转化为解题策略.

