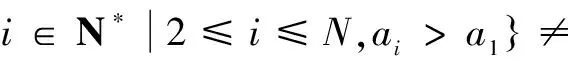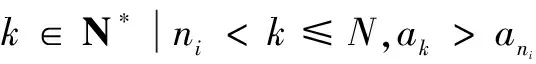赏析2016年高考新定义型创新题

虞 懿

(浙江省金华市第六中学，321000)

○高考复习研究○

赏析2016年高考新定义型创新题

虞 懿

(浙江省金华市第六中学，321000)

新定义型创新题常以“新定义”为载体考查学生学习新知识的能力,特别是能将所学知识与方法迁移到不同情境中,进而考查学生的理性思维和数学素养.下面采撷几道2016年高考数学试题中出现的新定义型创新题并予以解析,旨在探索题型规律,揭示解题方法.

一、定义新数列

数列是高中数学非常重要的内容,更是高考考查的重点. 有些创新题目定义了新的数列,在教材上没有出现过,对学生的理解能力、知识的迁移能力提出了较高的要求.

例1 (2016年全国高考题)定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有( )

(A)18个 (B)16个

(C)14个 (D)12个

解析 由题意可得a1=0,a8=1,a2,a3,…,a7中有3个0,3个1,且满足对任意k≤8,都有a1,a2,…,ak中0的个数不少于1的个数,利用列举法可得不同的“规范101数列”有00001111,00010111,00011011,00011101,00100111,00101011,00101101,00110011,00110101,01000111,01001011,01001101,01010011,01010101,共14个.

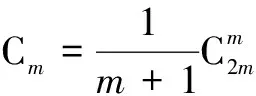
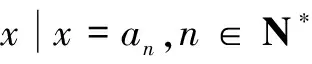
(1)若an=2n-1,bn=4n-2,判断{an}与{bn}是否为无穷互补数列,并说明理由;

(2)若an=2n且{an}与{bn}是无穷互补数列,求数列{bn}的前16项的和;

(3)若{an}与{bn}是无穷互补数列,{an}为等差数列且a16=36,求{an}与{bn}得通项公式.

解析 (1)因为4∉A,4∉B,所以4∉A∪B,从而{an}与{bn}不是无穷互补数列.

(2)因为a4=16,所以b16=16+4=20，于是数列{bn}的前16项的和

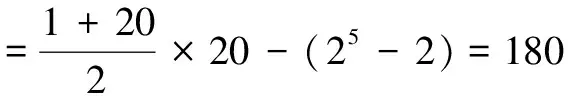
(3)设{an}的公差为d,d∈N*,则

a16=a1+15d=36，

由a1=36-15d≥1,得d=1或2.

若d=1,则a1=21,an=n+20,与“{an}与{bn}是无穷互补数列”矛盾;

若d=2,则a1=6,an=2n+4,

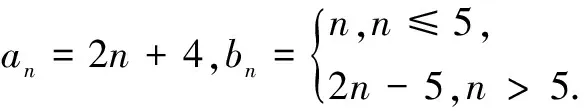
评注 要证明一个结论不正确,只要举出一个反例即可,而要证明结论正确,必须经过严格的推理论证.

二、 定义新性质

例3 (2016年山东高考题)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )

(A)y=sin x (B)y=ln x

(C)y=ex(D)y=x3

解析 设函数y=f(x)的图象上两点P(x1,y1),Q(x2,y2),则由导数的几何意义可知,点P,Q处切线的斜率分别为k1=f ′(x1),k2=f ′(x2).若函数具有T性质,则k1·k2=f ′(x1)·f ′(x2)=-1.

对于选项A,f ′(x)=cos x,显然k1·k2=f ′(x1)·f ′(x2)=-1有无数组解,所以该函数具有T性质;

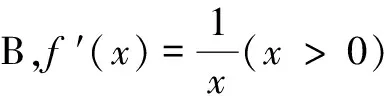
对于选项C,f ′(x)=ex>0,显然k1·k2=ex1·ex2=-1无解,故该函数不具有T性质;

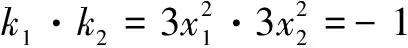
故选A.

评注 本题易出现的错误是不能正确理解新定义函数的性质,尤其是忽视函数定义域的取值范围,导致判断错误.

三、 定义新概念

此类题型往往用简洁抽象的语言给出一个新概念,没有太多的解释,要求学生自己仔细揣摩、体会和理解新定义的概念.

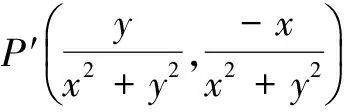
① 若点A的“伴随点”是点A′,则点A′的“伴随点”是点A;

② 单位圆的“伴随曲线”是它自身;

③ 若曲线C关于x轴对称,则其“伴随曲线”C′关于y轴对称;

④ 一条直线的“伴随曲线”是一条直线.

其中的真命题是______(写出所有真命题的序列).

对于②,设单位圆上任意一点A(cos t,sin t),则其“伴随点”为A′(sin t,-cos t),显然点A′在单位圆上,所以②正确;

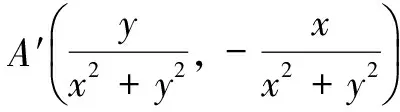
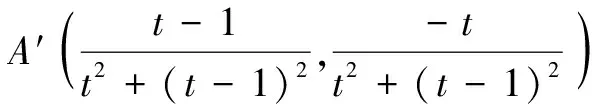
消去参数t,得x2+y2+x+y=0,所以直线y=x-1的“伴随曲线”为圆,所以④错.故填② ③.

评注 本题考查考生对新定义的理解和应用、圆的参数方程及其应用,意在考查考生的转化与化归能力和逻辑思维能力.

四、定义新符号

例5 (2016年全国高考题)Sn为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lg an],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1.

(1)求b1,b11,b101;

(2)求数列{bn}的前1 000项和.

解析 (1)设{an}的公差为d,由已知，有7+21d=28,解得d=1，所以{an}的通项公式为an=n.于是b1=[lg 1]=0,b11=[lg 11]=1,b101=[lg 101]=2.

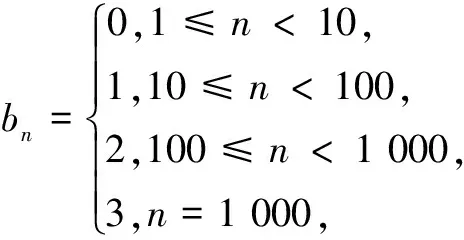
所以数列{bn}前1 000项和

S1 000=1×90+2×900+3×1=1 893.

评注 符号函数[x]是一个非常重要的数学概念,其定义和性质非常简单.正因为如此,在解决与之相关的问题时,可以依据的命题、法则不多,规律性不明显,但解法变化大,灵活性强，需要用到多种数学思想方法,其中较为常见的有分类讨论(例如对区间进行划分)、命题转换(例如等式转化为不等式)、数形结合等.

例6 (2016年浙江高考题)已知a≥3,函数F(x)=min{2|x-1|,x2-2ax+4a-2},

(1)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围;

(2)(i)求F(x)的最小值m(a);

(ii)求F(x)在区间[0,6]上的最大值M(a).

解析 (1)由于a≥3,故当x≤1时,(x2-2ax+4a-2)-2|x-1|=x2+2(a-1)(2-x)>0,

故当x>1时,(x2-2ax+4a-2)-2|x-1|=(x-2)(x-2a).

所以,使得等式F(x)=x2-2ax+4a-2成立的x的取值范围为[2,2a].

(2)(i)设函数f(x)=2|x-1|,g(x)=x2-2ax+4a-2,则

f(x)min=f(1)=0,

g(x)min=g(a)=-a2+4a-2.

所以,由F(x)的定义知

m(a)=min{f(1),g(a)},

(ii)当0≤x≤2时,

F(x)≤f(x)≤max{f(0),f(2)} =2=F(2)；

当2≤x≤6时,

F(x)≤g(x)≤max{g(2),g(6)} =max{2,34-8a} =max{F(2),F(6)}.

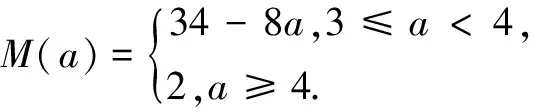
评注 数学符号是数学语言简约性的表现,在教材的正文部分(例、习题除外)没有正式定义的符号都是新符号.

五、 定义新集合

定义一个新集合,其元素满足某些条件,解此类问题旨在考查对集合中元素特征的研究以及数学解题思想的运用能力.

例7 (2016年北京高考题)设数列A:a1,a2,…,aN(N≥2).如果对小于n(2≤n≤N)的每个正整数k都有ak

(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;

(2)证明:若数列A中存在an使得an>a1,则G(A)≠∅;

(3)证明:若数列A满足an-an-1≤1(n=2,3,…,N),则G(A)的元素个数不小于aN-a1.

解析 (1)G(A)的元素为2和5(过程略).

(2)因为存在an使得an>a1,所以

因此m∈G(A),从而G(A)≠∅.

(3)当aN≤a1时,结论成立.以下设aN>a1，由(2)知G(A)≠∅.

设G(A)={n1,n2,…,np},n1

如果Gi≠∅,取mi=minGi,则对任意1≤k

又np是G(A)中的最大元素,所以Gp=∅.

从而对任意np≤k≤N,ak≤anp,特别地,aN≤anp.

对i=0,1,…,p-1,ani+1-1≤ani，因此

ani+1=ani+1-1+(ani+1-ani+1-1)≤ani+1，

因此G(A)的元素个数p不小于aN-a1.

评注 本题主要考查考生的阅读理解能力,逻辑思维能力,分析和解决问题的能力以及创新意识.这道题情境新颖,运算量小,思维量大,有效考查了考生数学思维的敏锐性、严谨性、深刻性与创造性等思维品质,且区分度很好.

结合上述高考试题,可归纳出新定义型创新题的求解通常分三大步骤进行:第一，对新定义进行信息提取,确定化归方向;第二，对新定义所提取的信息进行加工,探究解决方法;第三，对新定义中提取的信息进行转换,有效地输出.其中对新定义信息的提取和化归转化是求解的关键,也是求解的难点.