基于分形理论的磨粒磨损预测模型
丁雪兴,张正棠,任琪琛,白崇辉,王平西
(兰州理工大学石油化工学院,甘肃兰州 730050)
基于分形理论的磨粒磨损预测模型
丁雪兴,张正棠,任琪琛,白崇辉,王平西
(兰州理工大学石油化工学院,甘肃兰州 730050)
为了求解在粗糙表面上磨粒磨损的磨损率,在分形接触模型的基础上,利用塑性变形磨损理论推导了基于分形参数的磨损率模型,并建立了磨损率与分形维数、材料性能常数、磨屑概率之间的关系,从而反映出材料的磨损规律。从分析结果可以看出,当分形维数处在某一区间内时,随着分形维数的变化,磨损率先减小后增大;最优分形维数为1.5,此时磨损率最小。当分形维数保持不变时,随着尺度常数、概率常数的增大磨损率也随之增大;而随着材料性能常数的增大磨损率减小。当其他各参数都保持恒定时,接触面积越大磨损率也变大。该模型的建立为进一步研究粗糙表面的摩擦、磨损与润滑具有重要意义。
粗糙表面;磨粒磨损;塑性变形;磨损率
磨损是摩擦副的上下表面在相互接触摩擦时,表面的划伤或者破坏。很多时候,磨损是粗糙表面微凸体之间相互接触作用而引起的。早期,人们通过研究磨损的机理将磨损粗略地进行了划分。在这几种磨损中,磨粒磨损是最普遍也是危害最大的一种磨损形式,据统计,在生产生活中因磨粒磨损所造成的损失比例是非常大的,因而对磨粒磨损的研究是必要的。一般来说,磨粒磨损的机理是硬的颗粒或者硬的凸起物冲刷材料表面而引起材料脱落的过程,即磨粒的犁沟作用,微观切削过程。对此,人们对粗糙表面的磨粒磨损进行了大量研究,提出了磨粒磨损的发生机理,并建立了各种磨损模型,旨在揭示磨损规律和磨损的危害程度,从而寻找方法控制磨损过程,以降低磨损。
在最初的研究中,国内外学者就粗糙表面间的磨粒磨损进行研究,主要基于统计参数的接触模型,如G-W模型[1]、W-T模型[2]等,而以前的模型中表面特征参数众多,尤其对采样长度以及仪器分辨率的依赖性非常大,这样得出的结果也就有一定的偏差[3]。一般从微观上看到的工程表面都是粗糙不平的,很难进一步观测和确定,然而分形理论的引入改变了以往的看法,用分形参数可以准确细致地分析表征粗糙表面的形貌特征。分形理论中分形维数是一个反映粗糙表面不规则程度和准确描述空间能力的度量参数,并且对粗糙表面形貌和接触特性进行分析和描述。到目前为止,分形理论被广泛用于摩擦副表面形貌的描述和接触特性的研究,提出了粗糙表面弹塑性M-B接触模型[4]以及M-B修正模型[5],并基于以上模型对摩擦磨损进行预测,提出了摩擦磨损模型[6]以及对滑动摩擦表面温度分布[7,8]进行了确定。这些经典的分形接触模型在一定程度上客观地描述了接触力与真实接触面积之间的关系,对分析摩擦、磨损、润滑和密封有着重要的作用。
丁雪兴等[9]考虑到以往分形接触模型的一些不足,如M-B分形接触模型中,单个微凸体的接触面积与其变形量之间的变化关系是相反的,而实际上微凸体变形量与接触面积的变化是一致的,重新构建滑动粗糙表面间的分形接触模型。据此我们根据这一重新构建的分形接触模型,结合塑性变形机理推导了磨粒磨损、磨损率模型以及磨损率的计算,并建立磨损率与分形维数、特征尺度常数和概率常数之间的关系,从而反映粗糙表面摩擦副之间的规律和特性。
1 微凸体的接触变形与塑性变形载荷
1.1 微凸体的接触变形
在过去的分形接触模型中都是先进行一些简化,这种简化为粗糙表面与刚性理想平面的接触,而在研究中采用不同的简化,即王新华等[10]对磨粒磨损的简化,磨粒磨损中刚性粗糙表面与理想软平面的接触。
在这里同样假设粗糙表面是各项同性的,忽略相邻微凸体之间的相互作用,粗糙面上的波峰为球形峰,所有接触点随机分布。变形分析中采用文献[9]中提到的分形接触模型,利用基地长度来弥补微凸体中的空隙,从而提高精确度。
由W-M函数可知摩擦副微凸体粗糙性的变化趋势是余弦波,还没变形时微凸体为
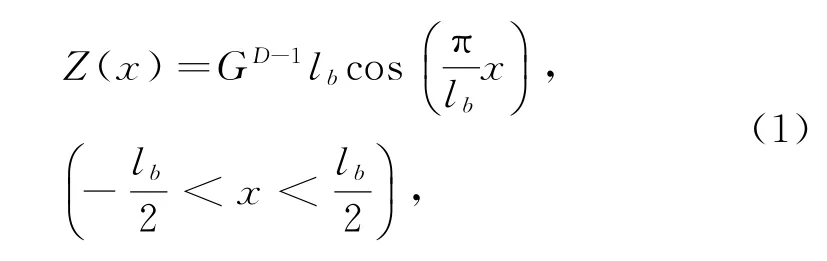
由此得微凸体曲率半径为
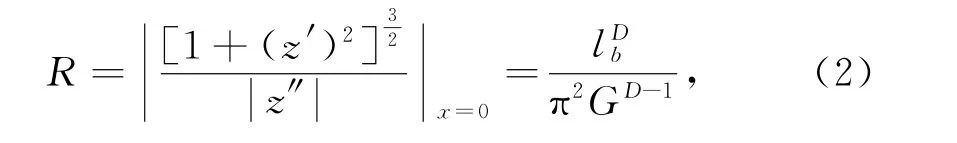
微凸体实际变形量为
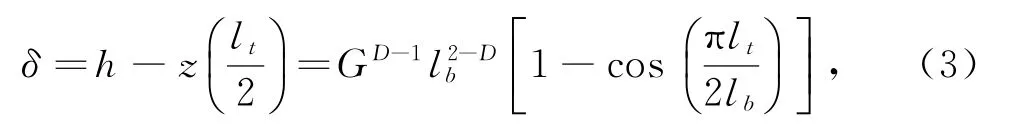
其中:h为微凸体顶端到底部的距离。
为了得到作用在微凸体的最大接触压力,这里采用Hertz弹性接触理论[11]:
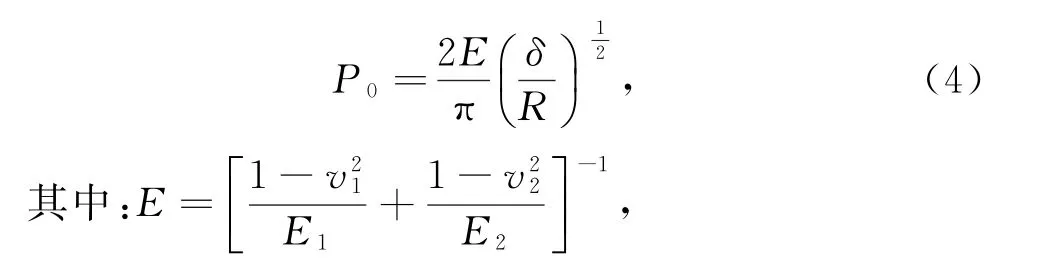
其中:E1、E2为材料的弹性模量;ν1、ν2为材料的泊松比。
微凸体临接触压力关系为
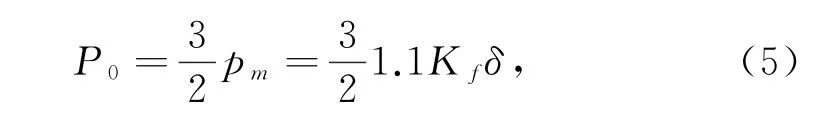
其中:Kf为摩擦力修正因子;σy为摩擦副上下表面材料中较软材料的屈服强度。
Kf的确定公式为
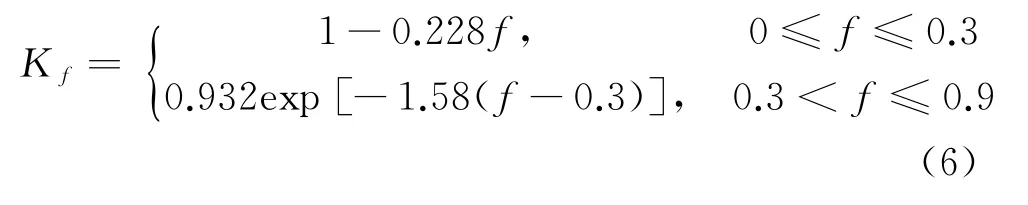
由式(2)、式(3)、式(5)可知,微凸体变形开始屈服的临界变形量为
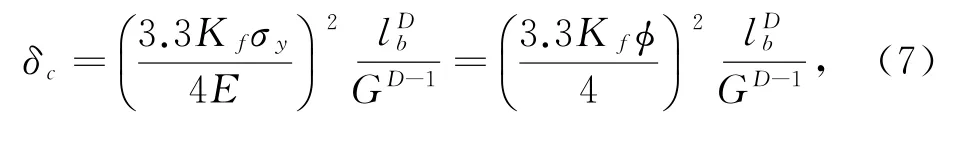
所以由式(2)、式(7)得临界变形面积
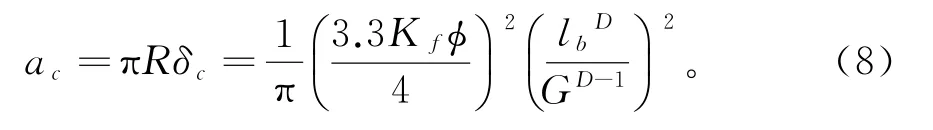
在滑动摩擦状态下,单个微凸体处在塑性变形下的接触压力[12]为
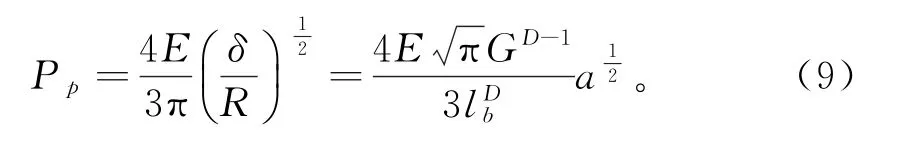
1.2 接触点处产生的塑性变形的载荷
在这里采用Wang等[7]的研究结果:
最大微接触面积为
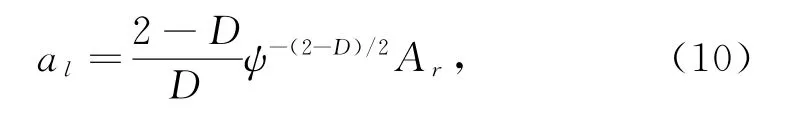
由超越方程
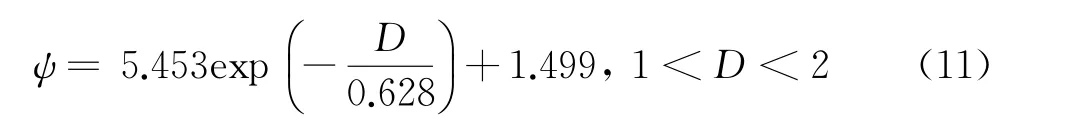
可知当a<ac时,处于塑性变形状态。
这里根据上述假设把微凸体看作是球形峰,假设波长为l,接触面积为并假设则单个球形峰的面积为
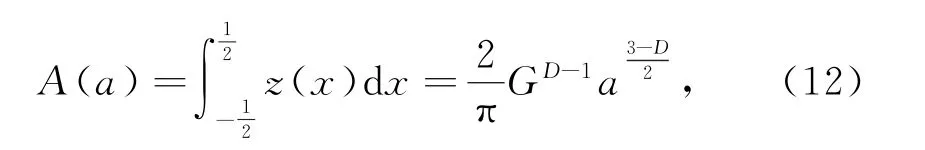
球形峰上的塑性载荷为

则在整个接触面上产生的塑性变形的载荷为
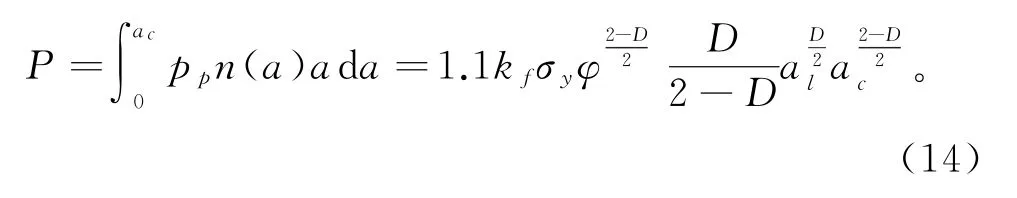
2 处于塑性变形下的磨粒磨损模型
根据磨粒磨损机理,当刚性粗糙平面与理想软平面在正向载荷作用下,粗糙平面上的刚性球峰挤入软平面中,在该位置产生变形,由于摩擦副的上下表面是相对运动的,这样就会在软平面上沿着滑动方向形成犁沟,而这些犁沟上的磨粒在摩擦反复作用下,两侧凸起的部分很快就折断了,产生磨屑,这样外界硬颗粒或者对磨表面上的硬突起物在摩擦过程中就会引起表面材料的脱落,从而引起磨粒磨损。在粗糙表面的单个球峰上沿滑动方向滑动一段距离时,假设这个距离为L,滑过距离l所产生的磨屑的体积为H(a),则单个微凸体的磨损量为
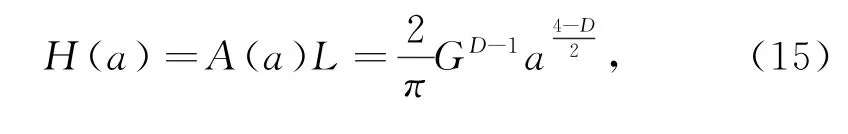
整个接触面上产生磨屑的体积为
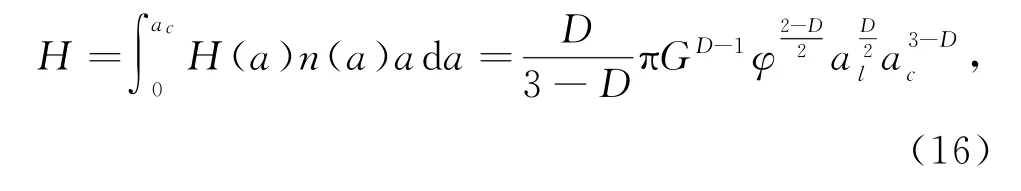
当有V(a)的磨屑体积产生时,在摩擦副上滑过的距离为
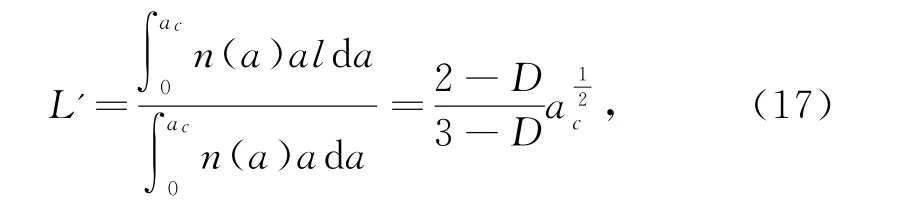
由此得接触面上总的磨损率为
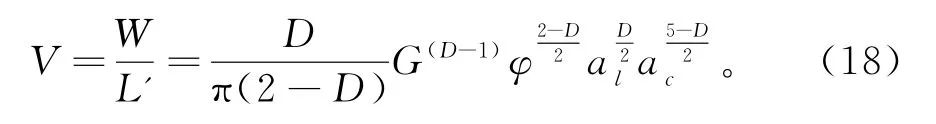
将式(10)、式(13)代入式(18)中得:

在上述推导中,是整个接触面上都产生磨屑,而在实际生产中只是个别微凸体会产生磨屑,因此,假设产生磨屑的概率为ζ,则在整个接触面上磨损量为
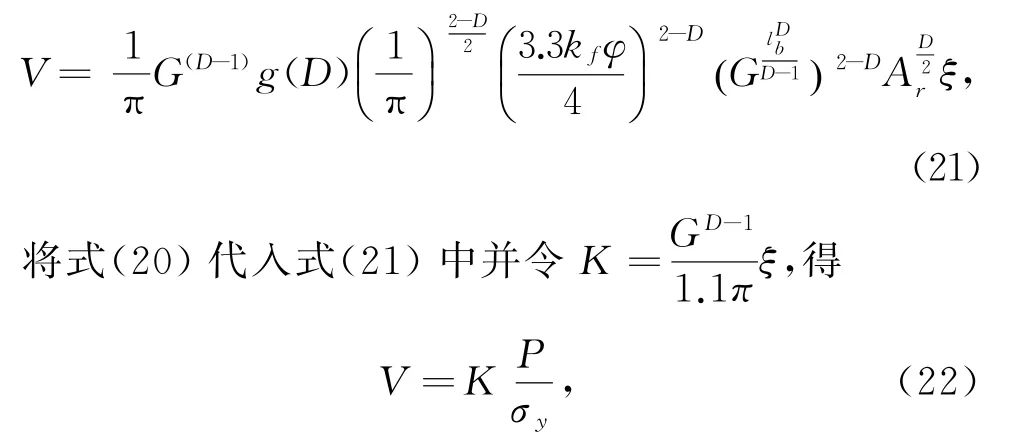
其中:K为磨损系数;σy为材料硬度。
在式(22)中可以看出该磨粒磨损公式与传统的磨损公式基本一样,即磨损率与法向载荷成正比,与材料的屈服极限成反比。
为了分析方便起见无量纲化:
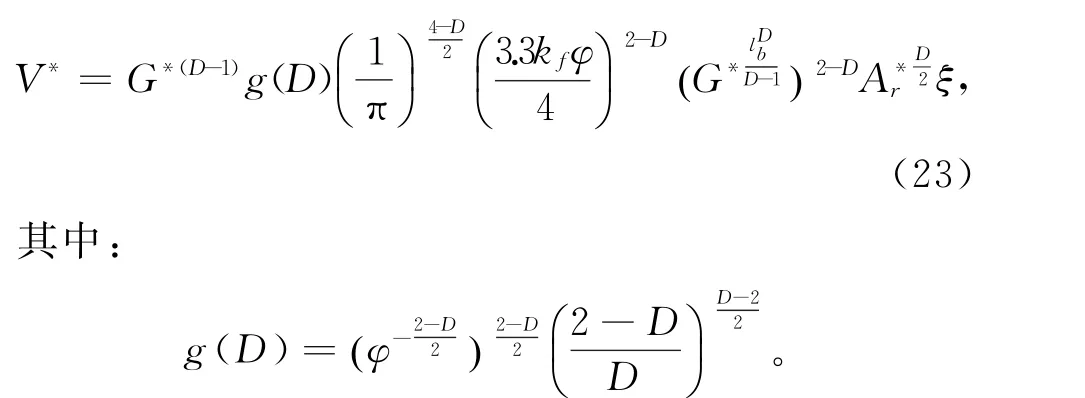
式(23)为动态方程,材料的磨损率随G、D、φ、ζ等参数的变化而变化。
3 磨损率的影响因素
3.1 分形维数的影响
为了能确定分形维数与磨损率之间的关系,在这里将式(23)两边同取对数,得到不同接触面积时磨损率与分形维数的关系,如图1所示。从图1中可以看出,当分形维数1.1≤D<1.5时,随着分形维数变化,磨损率先减小后增大;当分形维数1.5<D≤1.9时,磨损率随着分形维数的增大而缓慢增大,这种增长的幅度很小。当分形维数D=1.5时,磨损率达到预期值。另外,接触面积越大磨损率越大。

图1 不同接触面积时磨损率lg V∗与分形维数D的关系Fig.1 The relationship between wear rate lg V∗and fractional dimension D with different contact area
3.2 尺度系数的影响

图2 不同尺度系数时磨损率lg V∗与接触面积lg Ar∗的关系Fig.2 The relationship between wear rate lg V∗and contact area lg Ar∗with different scales coefficient
3.3 材料性能常数的影响
我们同样令D=1.4,G∗=10-9,ζ=0.1,得到不同材料性能常数下磨损率与接触面积的关系见图3。从图3中可以看出,磨损率与材料性能常数的变化正好相反,这是因为材料的性能常数综合反映了材料的硬度,材料的硬度越好,越不容易引起磨损。
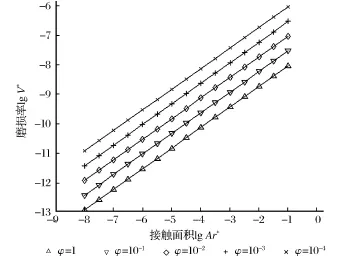
图3 不同材料性能常数时磨损率lg V∗与接触面积lg Ar∗的关系Fig.3 The relationship between wear rate lg V∗and contact area lg Ar∗with different material property constant
3.4 磨损概率常数的影响
同样令D=1.4,G∗=10-9,φ=0.01,从而得到不同磨损概率常数下磨损率与接触面积的关系见图4。很明显,磨损率随着磨损概率常数的增大而增大,这是因为磨损概率常数ζ越大,微凸体接触的概率也越大,磨损越严重,因此,磨损率就越高。
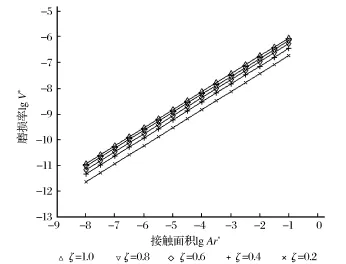
图4 不同磨损概率常数时磨损率lg V∗与接触面积lg Ar∗关系Fig.4 The relationship between wear rate lg V∗and contact area lg Ar∗with different wear probability constant
4 结论
(1)从磨损率分形模型中得知磨损率与各分形参数之间的关系,全面反映了材料的磨损规律和磨损率的变化情况。而这些变化和规律都与粗糙表面的接触有关,不同的参数有不同的磨损率。以后可以通过测量分形参数来预测材料的磨损程度,进而更好地控制磨损。
(2)后续工作中将对研究内容进行实验验证,进一步完善研究。因为粗糙表面情况非常复杂,涉及到的参数众多。
[1] Morag Y,Etsion I.Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces[J].Wear,2007,262(5-6):624-629.
[2] Greenwood J A,Williamson J B P.Contact of Nominally Flat Surfaces[J].Proceedings of the Royal Society of London.Series A,Mathematical and Physical Sciences,1966,295(1442): 300-319.
[3]Greenwood J A,Tripp J H.The Elastic Contact of Rough Spheres[J].ASME Journal of Applied Mechanics,1967,34 (1):153-159.
[4] Jumdar A,Bhushan B.Fractal Model of Elastic-plastic Contact Between Rough Surfaces[J].ASME,Journal of Tribology, 1991,113(1):1-11.
[5] Majumdar A,Bhushan B.Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surface[J].Journal of Tribology(ASME),1990,112:1-11.
[6] Zhou G Y,Leu M C,Blackmore D.Fractal Geometry Model for Wear Prediction[J].Wear,1993,170(1):1-14.
[7]Wang S,Komvopoulos K.Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime:PartⅠ-Elastic Contact and Heat Transfer Analysis[J].Journal of Tribology,1994,116(4):812-823.
[8]Wang S,Komvopoulos K.Fractal Theory of the Interfacial Temperature Distribution in the Slow Sliding Regime:PartⅡ-Multiple Domains,Elastoplastic Contacts and Applications [J].Journal of Tribology,1994,116(4):824-832.
[9] 丁雪兴,严如奇,贾永磊.基于基底长度的粗糙表面分形接触模型的构建与分析[J].摩擦学学报,2014,34(4):341-347.
[10] 王新华,张嗣伟,樊启蕴.基于分形理论的磨粒磨损模型[J].润滑与密封,2002,27(3):2-4.
[11] Johnson K L.Contact mechanics[M].London:Cammbeidge University Press,1985.
[12] 董霖,张永相.M-B弹塑性接触模型的修正[J].四川工业学院学报,2001,20(2):4-7.
Abrasive Wear Prediction Model Based on Fractal Theory
Ding Xuexing,Zhang Zhengtang,Ren Qichen,Bai Chonghui,Wang Pingxi
(College of Petrochemical Engineering,Lanzhou Universe of Technology,Lanzhou730050,China)
For the purpose of getting wear rate of abrasive wear on rough surface,based on fractal contact model and by use of plastic deformation,this text here deduce wear rate model on basis of fractal parameter and builds the relationship between wear rate and fractal dimension,material property constant and wear debris probability which can reflect material wear rule.From the result,when fractal dimension is in some interval,the wear rate first reduces and then increases with fractal dimension changing;when the optimized fractional dimension is1.5,wear rate is minimum.When fractional dimension keeps constant,wear rate increases with measure constant and probability constant increasing;but wear rate reduces with material property constant increasing.When other parameters keep constant,wear rate increases with contact area increasing.It is of great importance to build this model for further studying friction,wear and lubrication of rough surface.
Rough surface;Abrasive wear;Plastic deformation;Wear rate
TH117
:A
:1004-0366(2016)05-084-05
2015-09-07;
:2015-10-28.
丁雪兴(1964-),男,江苏苏州人,博士,教授,研究方向为流体动密封.E-mail:xuexingding@163.com.
张正棠.E-mail:15709440802@163.com.
Ding Xuexing,Zhang Zhengtang,Ren Qichen,et al.Abrasive Wear Prediction Model Based on Fractal Theory[J].Journal of Gansu Sciences,2016,28(5):84-88.[丁雪兴,张正棠,任琪琛,等.基于分形理论的磨粒磨损预测模型[J].甘肃科学学报,2016,28(5):84-88.]
10.16468/j.cnkii.ssn1004-0366.2016.05.020.

