基于系统码信息位搜索的二元(24,12,8)Golay译码算法*
江宝安
(重庆邮电大学 移通学院,重庆 400065)
基于系统码信息位搜索的二元(24,12,8)Golay译码算法*
江宝安
(重庆邮电大学 移通学院,重庆 400065)
针对(24,12,8)Golay译码问题,提出一种新的基于系统码信息位搜索的译码算法。该算法定义新的校正子,由接收到的信息位计算监督位,校正子由信息位计算出的监督位和接收的监督位相加共同确定,且具有可分性。译码只搜索信息位错误,不搜索监督位错误,与在整个码空间搜索错误位的一般线性分组码译码算法相比,该算法大幅降低了计算量,特别对纠多个错误位的(24,12,8)Golay码更加有效,同时也适用于循环码、BCH码和LDPC码的译码。
纠错码;线性分组码;校正子;译码算法;循环码
0 引 言
二元(23,12,7)Golay码是线性分组码中的循环码,最小距离为7,,表示下限取整,能够纠正23位码字中的任何3个或更少的随机差错的组合。
Golay循环码在伽罗华域GF(2)的因式分解为:
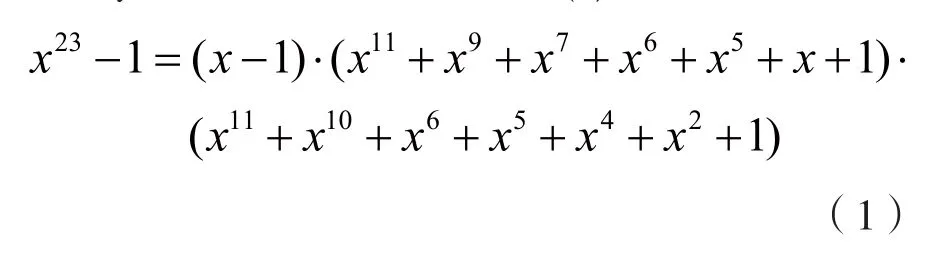
生成多项式为:
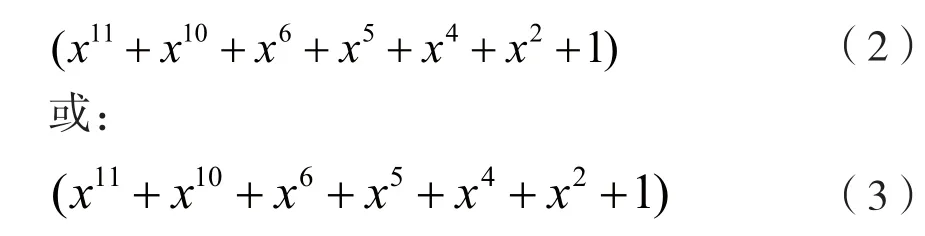
由于满足完备码(Perfect Code)公式:

可见,二元(23,12,7)Golay码是唯一的可纠3个错误的完备码,具有良好的代数结构,在深空探测及通信中具有重要的应用价值。
(23,12,7)Golay码可以通过对每个码字增加一位总的奇偶校验位来进行扩展,生成(24,12,8)码。(24,12,8)码最小距离为8,能够纠正所有含3个或更少差错的错误模式,并能检测所有含4个差错的错误模式。由于(24,12,8)Golay码码长为24位,3个字节,在某些应用方面更简便,也更常用。
1 新的系统码译码算法
一般的Cb(n,k,d)系统码生成矩阵为G=[Ik×kPk×(n-k)],其中Ik×k为k阶单位阵,P(n-k)×k为监督矩阵,简写为G=[I P]。因此,有:
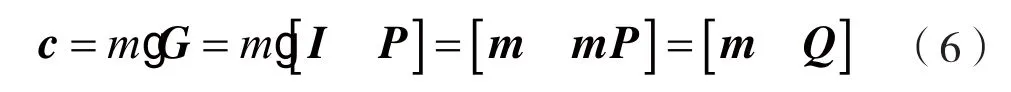
其中m表示信息位。
由于存在信道噪声,所以接收码为:
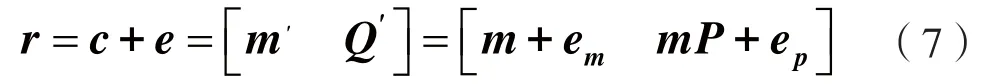
其中em表示信息位错误,ep表示监督位错误。
定义新的校正子S(Syndrome),见式(8),如图1所示。
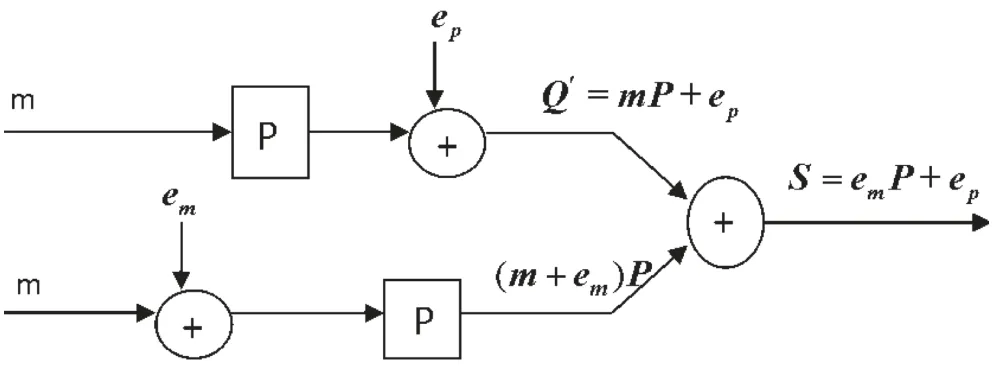
图1 校正子S

故校正子S由信息位错误em和校验位错误ep共同确定,且具有可分性。译码器的主要任务就是如何从S中基于最小错误准则得到em,从而译出:

由最小错误概率准则,译码算法如下:
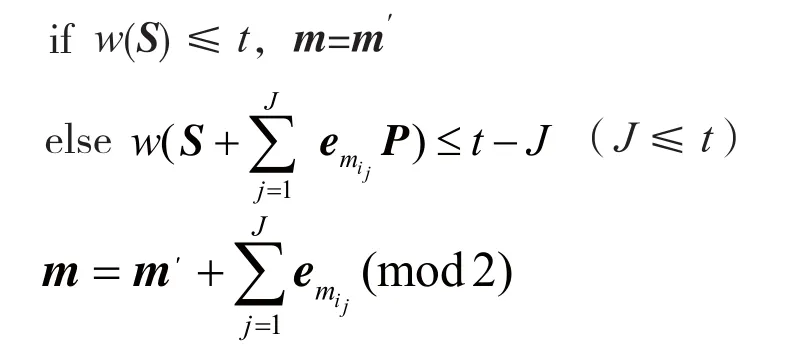
需说明的是,这里w(·)表示求Hamming权重。
2 二元扩展(24,12,8)Golay的译码算法
二元(24,12,8)Golay编码所用的生成矩阵见式(10):

二元(24,12,8)Golay相应的监督矩阵见式(11)。
任设二元(24,12,8)Golay码,见式(12)。
假设接收码为式(13),信息位有2个错误位,监督位有1位错误。先用接收码的前12位信息位乘监督矩阵P,再加接收码的后12位监督位,得校正子S,由校正子S的Hamming权重确定信息位是否有错,见式(14)。


满足式(16)的hamming权值小于1:
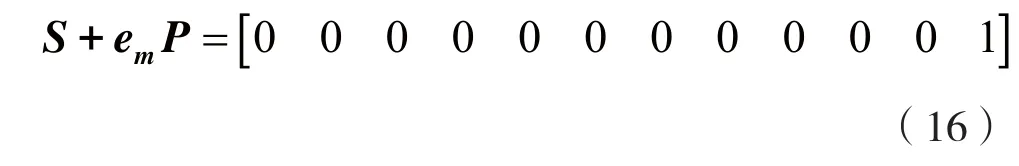
所以,可以直接纠正信息位错误,而不用搜索和纠正监督位错误。
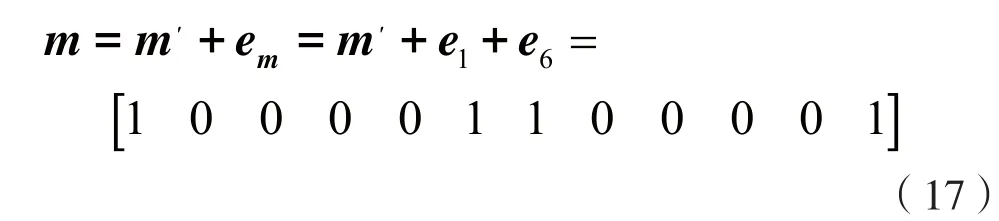
假设接收码为式(18),信息位有3个错误位,监督位没有错误:

满足式(21)的hamming权值小于等于0:

所以,可以直接纠正信息位错误,而不用搜索和纠正监督位错误。
类似地,其他的二元(24,12,8)Golay的误码形式只要在纠错范围内,都可以以相同的算法纠正。
3 结 语
本算法利用系统码的搜索信息位错误位,C(n,k,d)中纠正t信息位错误最多搜索次。对纠多个错误位的系统码,信息位相对整个码长更短。相对于一般在整个码空间搜索错误位的算法,本算法只搜索信息位错误,不搜索﹑不纠正监督位错误,极大地减少了计算量。同时,对能纠正3个错误位的二元(24,12,8)Golay码而言,与一般的译码算法相比,它明显减少了计算量。此外,由于能纠正多个错误位的循环码﹑BCH码和LDPC码本质上是线性分组码,有相应的等效系统码,所以本文提出的算法也适用于这些码的译码。
[1] Sweeney P.Error Control Coding.From Theory to Practice[M].New Jersey:W iley,2002:67-83.
[2] Jorge Castiñeira Moreira,Essentials of Error Control Coding[M].New Jersey:Wiley,2006:41-61.
(24,12,8)Golay Decoding Algorithm based on Searching Information Error of System Code
JIANG Bao-an
(University of Post and Telecommunication of ChongQing, Chongqing 400065, China)
A novel(24,12,8) Golay decoding algorithm based on searching information error of system code is proposed, which defines a new syndrome adding jointly by the received supervision bit and the supervision bits computing from the received information bits. The decoding algorithm only searches information-bit errors, no parity-bit errors. As compared with the general linear block-code decoding algorithm to search the entire code space error bits, this proposed decoding algorithm, could greatly reduce the amount of calculation, and is more effective for correcting multiple error bits of(24,12,8) Golay code, also applicable to decoding cyclic codes, BCH codes and LDPC codes.
Golay; linear block code; syndrome; decoding algorithm; cyclic code
TP393.03
A
1002-0802(2016)-11-1429-04
10.3969/j.issn.1002-0802.2016.11.003
江宝安(1974—),男,硕士,讲师,主要研究方向为信号处理与通信理论。

2016-07-20;
2016-10-24 Received date:2016-07-20;Revised date:2016-10-24

